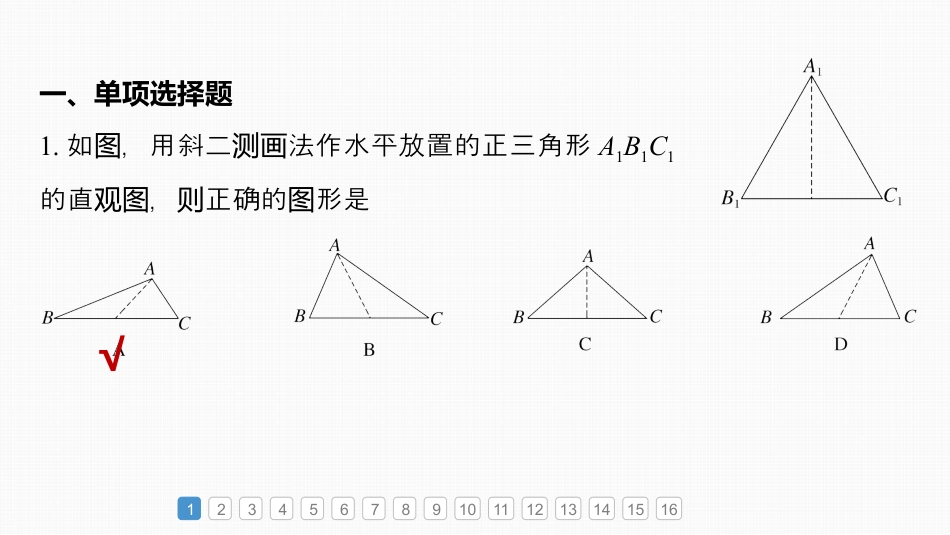
必刷小题13立体几何第七章立体几何与空间向量一、单项选择题1.如，用斜二法作水平放置的正三角形图测画A1B1C1的直，正确的形是观图则图12345678910111213141516√12345678910111213141516以B1C1所在直线为x，以轴B1C1上的高边为y建立坐系，轴标画对的应x′，y′，使角轴夹为45°，直画观图时与x平行的段轴线度保持不，长变与y平行的段度原的一半，然后去掉轴线长变为来助即可得到正三角形的直，如辅线观图图.2.下列四命中，正确的是个题A.各面都是全等四形的柱一定是正柱侧边棱棱B.角面是全等矩形的六面体一定是方体对长C.有面垂直于底面的柱一定是直柱两侧棱棱D.方体一定是直四柱长棱√1234567891011121314151612345678910111213141516于对A，底面是菱形的直平行六面体，足件但不是正柱；满条棱于对B，底面是等腰梯形的直柱，足件但不是方体；棱满条长C然；显错误方体一定是直四柱，长棱D正确.123456789101112131415163.平面外一点从P引平面相交的直，使与线P点交点的距离等于与1，足件的直可能有则满条线A.0或条1条B.0或无条数条C.1或条2条D.0或条1或无条数条点当P到平面的距离大于1，有足件的直；点时没满条线当P到平面的距离等于1，足件的直只有时满条线1；点条当P到平面的距离小于1，足件的直有无时满条线数条.√123456789101112131415164.已知m，n表示不同的直，两条线α，β表示不同的平面，下两个则列命中正确的是题A.若m∥α，n⊥β，m∥n，则α⊥βB.若m⊥n，m⊥α，n∥β，则α∥βC.若α⊥β，m⊥α，m⊥n，则n∥βD.若α⊥β，α∩β＝m，n⊥m，则n⊥β√12345678910111213141516于对A，由m∥α，m∥n，得到：若n∥α，过n的平面γ∩α＝l，则n∥l，又n⊥β，则l⊥β，l⊂α，则α⊥β，若n⊂α，又n⊥β，则α⊥β.上，综α⊥β，故A正确；于对B，若m⊥n，m⊥α，n∥β，则α与β相交或平行，故B错；误于对C，若α⊥β，m⊥α，m⊥n，则n与β相交、平行或n⊂β，故C；错误于对D，若α⊥β，α∩β＝m，n⊥m，则n与β相交或n⊂β，故123456789101112131415165.已知直线a，b，l和平面α，β，a⊂α，b⊂β，α∩β＝l，且α⊥β.于以下命，判正确的是对题断①若a，b面，异则a，b至少有一个与l相交；②若a，b垂直，则a，b至少有一个与l垂直.A.①是命，真题②是假命题B.①是假命，题②是命真题C.①是假命，题②是假命题D.①是命，真题②是命真题√12345678910111213141516于对①，若a，b都不与l相交，只有一可能，即则种a，b均平行于l，则a∥b，∴若a，b面，异则a，b至少有一个与l相交，故①正确；于对②，根据面面垂直的性定理得：质若a，b垂直，则a⊥β，或b⊥α，故a，b至少有一个与l垂直，故②正确.A.203cmB.15cmC.103cmD.20cm123456789101112131415166.(2023·徐州模拟)柱形玻璃杯中盛有高度圆为10cm的水，若放入一个玻璃球(球的半柱形玻璃杯壁的底面半相同径与圆内径)后，水恰好淹了玻璃球，玻璃球的半没则径为√12345678910111213141516根据意，玻璃球的体等于放入玻璃球后水柱的体去原水柱题积积减来的体；积玻璃球的半设径为r，即柱形玻璃杯的底面半圆径为r；放入一玻璃球后，水恰好淹玻璃球，个没则玻璃球的体积为43πr3，柱的底面面圆积为πr2，此水面的高度时为2r，所以43πr3＝πr2(2r－10)，解得r＝15(cm).7.蹴鞠，又名蹴球，等，蹴有用脚蹴、、的含，鞠最早系外踢圆踢蹋义包皮革、米糠的球内实.因而蹴鞠就是指古人以脚蹴、、皮球的活，蹋踢动似今日的足球类.2006年5月20日，蹴鞠已作非物文化为质遗产经国务院批准列入第一批家非物文化名国质遗产录.已知某鞠的表面上有五点个P，A，B，C，D恰好成一正四构棱锥P－ABCD，若的高该棱锥为8，底面边长为，鞠的表面则该积为A.64πB.100πC.132πD.144π12345678910111213141516√4212345678910111213141516正四棱锥P－ABCD的底面是正方形，底面边长为42，高为8，如图所示，所以正四棱锥P－ABCD的底面角的对线长为42×2＝8，正四外接球的半设棱锥径为R，则R2＝(8－R)2＋42，解得R＝5，所以球的表面积为S＝4π·R2＝4π×25＝100π，即鞠的表面该积为100π.8.某同学画“切面柱体圆”(用柱底面不平行的平面切柱，底...