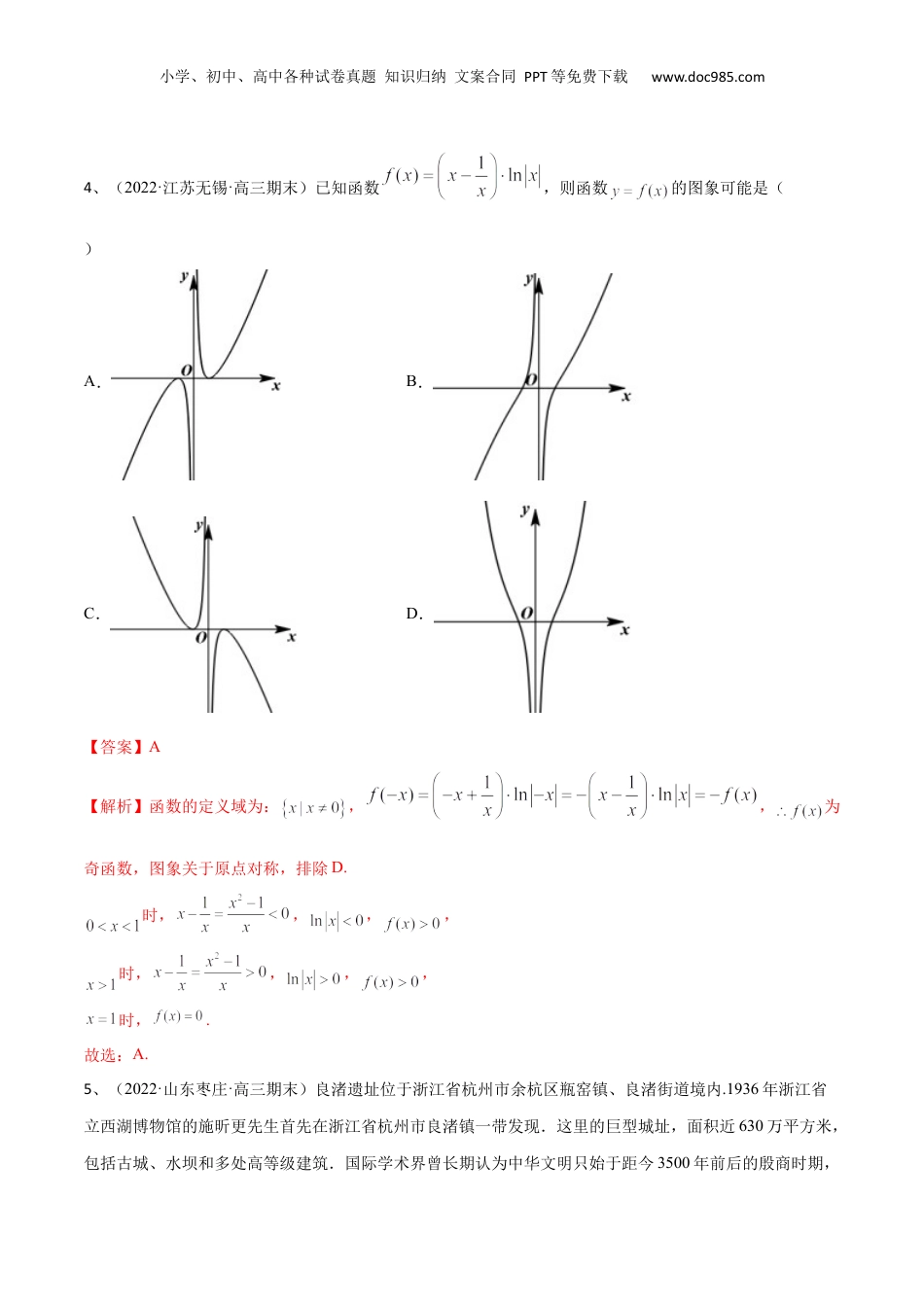
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第18讲章末检测三一、单选题1、（2022·山东烟台·高三期末）函数的定义域为（）A．B．C．D．【答案】C【解析】由已知可得，即，因此，函数的定义域为.故选：C.2、(2022·江苏淮安市六校第一次联考)已知函数f(x)＝，则f(－2022)＝（）．A．－2B．2C．5D．3【答案】A【解析】由题意可知，f(－2022)＝f(－2019)＝…＝f(－2022)＝f(0)＝log3(0＋1)－2＝－2．3、（2022·江苏如皋·高三期末）“函数f(x)＝sinx＋(a－1)cosx为奇函数”是“a＝1”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】C【解析】函数f(x)＝sinx＋(a－1)cosx为奇函数,则，化简得：，故，当时，f(x)＝sinx是奇函数，因此“函数f(x)＝sinx＋(a－1)cosx为奇函数”是“a＝1”充要条件，故选:C.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4、（2022·江苏无锡·高三期末）已知函数，则函数的图象可能是（）A．B．C．D．【答案】A【解析】函数的定义域为：，，为奇函数，图象关于原点对称，排除D.时，，，，时，，，，时，.故选：A.5、（2022·山东枣庄·高三期末）良渚遗址位于浙江省杭州市余杭区瓶窑镇、良渚街道境内.1936年浙江省立西湖博物馆的施昕更先生首先在浙江省杭州市良渚镇一带发现．这里的巨型城址，面积近630万平方米，包括古城、水坝和多处高等级建筑．国际学术界曾长期认为中华文明只始于距今3500年前后的殷商时期，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2019年7月6日，中国良渚古城遗址被列入世界遗产名录，这意味着中国文明起源形成于距今五千年前，终于得到了国际承认！2010年，考古学家对良渚古城水利系统中一条水坝的建筑材料（草裏泥）上提取的草茎遗存进行碳14年代学检测，检测出碳14的残留量约为初始量的．已知经过x年后，碳14的残余量，碳14的半衰期为5730年，则以此推断此水坝大概的建成年代是（）．（参考数据：）A．公元前2893年B．公元前2903年C．公元前2913年D．公元前2923年【答案】B【解析】碳14的半衰期为5730年，，当时，，，2010年之前的4912年是公元前2902年，以此推断此水坝大概的建成年代是公元前2903年.故选：B.6、（2022·江苏通州·高三期末）函数y＝[x]广泛应用于数论、函数绘图和计算机领域，其中[x]为不超过实数x的最大整数，例如：[－2.1]＝－3，[3.1]＝3.已知函数f(x)＝[log2x]，则f(1)＋f(3)＋f(5)＋…＋f(210＋1)＝（）A．4097B．4107C．5119D．5129【答案】B【解析】由题意时，，，在上奇数共有个，，，，设，则，相减得：，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，所以．故选：B．7、（2022·山东烟台·高三期末）若定义在R上的奇函数在上单调递减，且，则满足的x的取值范围是（）A．B．C．D．【答案】C【解析】由题意，定义在R上的奇函数在上单调递减，且，则在上单调递减，且，，因为，当时，即，此时满足不等式；当时，即，可得，且满足，则，解得；当时，即，可得，且满足，则，解得，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com综上可得，不等式的解集为.故选：C.8、(2022·江苏南京市二十九中学高三10月月考)设，，，则的大小关系为（）A.B.C.D.【答案】B【解析】，，，，，，即，；，即，；，即，；，即.设，则，当时，，又，，，在上单调递减，，即当时，，，，即.综上所述：.故选：B.二、多选题9、（2022·江苏海安·高三期末）下列函数在区间上单调递增的是（）A．B．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．D．【答案】BC【解析】对于A：为开口向上的抛物线，对称轴为，所以在区间上单调递减，故选项A不正确；对于B：的定义域为，将的图象向右平移一个单位可得，因为在上单调递增，向右平移一个单位可得在上单调递增，所以在区间上单调递增，故选项B正确；对于C：，所以在区间上单调递增，故选项C正确；对于D：是由和复合而成，因为单调递减，在区间上单调...