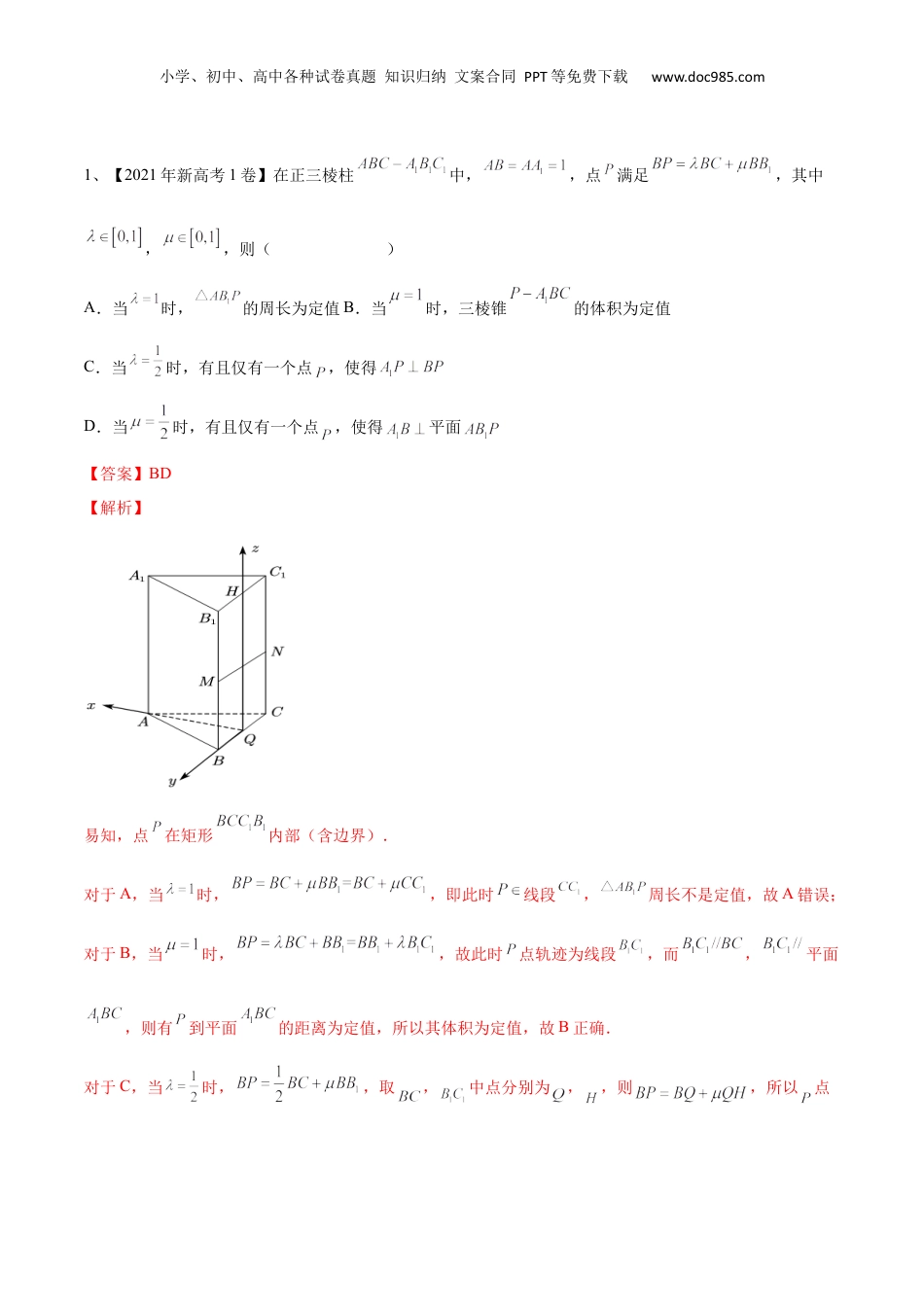
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第54讲空间角与距离的计算（1）1.直线的方向向量和平面的法向量(1)直线的方向向量：如果表示非零向量a的有向线段所在直线与直线l平行或重合，则称此向量a为直线l的方向向量．(2)平面的法向量：直线l⊥α，取直线l的方向向量a，则向量a叫做平面α的法向量．2.空间位置关系的向量表示位置关系向量表示直线l1，l2的方向向量分别为n1，n2l1∥l2n1∥n2⇔n1＝λn2l1⊥l2n1⊥n2⇔n1·n2＝0直线l的方向向量为n，平面α的法向量为m,l∥α,n⊥m⇔n·m＝0l⊥α,n∥m⇔n＝λm平面α，β的法向量分别为n，m,α∥β,n∥m⇔n＝λmα⊥β,n⊥m⇔n·m＝03.异面直线所成的角3.设a，b分别是两异面直线l1，l2的方向向量，则a与b的夹角βl1与l2所成的角θ范围(0，π)a与b的夹角βl1与l2所成的角θ求法cosβ＝cosθ＝|cosβ|＝4.求直线与平面所成的角设直线l的方向向量为a，平面α的法向量为n，直线l与平面α所成的角为θ，则sinθ＝|cos〈a，n〉|＝.5.求二面角的大小(1)如图①，AB，CD是二面角α－l－β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈AB，CD〉①②③(2)如图②③，n1，n2分别是二面角α－l－β的两个半平面α，β的法向量，则二面角的大小θ满足|cosθ|＝|cos〈n1，n2〉|，二面角的平面角大小是向量n1与n2的夹角(或其补角)．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、【2021年新高考1卷】在正三棱柱中，，点满足，其中，，则（）A．当时，的周长为定值B．当时，三棱锥的体积为定值C．当时，有且仅有一个点，使得D．当时，有且仅有一个点，使得平面【答案】BD【解析】易知，点在矩形内部（含边界）．对于A，当时，，即此时线段，周长不是定值，故A错误；对于B，当时，，故此时点轨迹为线段，而，平面，则有到平面的距离为定值，所以其体积为定值，故B正确．对于C，当时，，取，中点分别为，，则，所以点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com轨迹为线段，不妨建系解决，建立空间直角坐标系如图，，，，则，，，所以或．故均满足，故C错误；对于D，当时，，取，中点为．，所以点轨迹为线段．设，因为，所以，，所以，此时与重合，故D正确．故选：BD．2、【2018年新课标2卷理科】在长方体中，，，则异面直线与所成角的余弦值为A．B．C．D．【答案】C【解析】以D为坐标原点，DA,DC,DD1为x,y,z轴建立空间直角坐标系，则,所以,因为，所以异面直线与所成角的余弦值为，选C.3、【2022年全国甲卷】在四棱锥P−ABCD中，PD⊥底面ABCD,CD∥AB,AD=DC=CB=1,AB=2,DP=❑√3．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：BD⊥PA；(2)求PD与平面PAB所成的角的正弦值．【解析】(1)证明：在四边形ABCD中，作DE⊥AB于E，CF⊥AB于F，因为CD/¿AB,AD=CD=CB=1,AB=2，所以四边形ABCD为等腰梯形，所以AE=BF=12，故DE=❑√32，BD=❑√DE2+BE2=❑√3，所以AD2+BD2=AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD=D，所以BD⊥平面PAD，又因PA⊂平面PAD，所以BD⊥PA；(2)如图，以点D为原点建立空间直角坐标系，BD=❑√3，则A(1,0,0),B(0,❑√3,0),P(0,0,❑√3)，则⃗AP=(−1,0,❑√3),⃗BP=(0,−❑√3,❑√3),⃗DP=(0,0,❑√3)，设平面PAB的法向量⃗n=(x,y,z)，则有{n→⋅AP→=−x+❑√3z=0n→⋅BP→=−❑√3y+❑√3z=0，可取⃗n=(❑√3,1,1)，则cos〈⃗n,⃗DP〉=⃗n⋅⃗DP¿⃗n∨¿⃗DP∨¿=❑√55¿，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以PD与平面PAB所成角的正弦值为❑√55.4、【2022年全国乙卷】如图，四面体ABCD中，AD⊥CD,AD=CD,∠ADB=∠BDC，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设AB=BD=2,∠ACB=60°，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成的角的正弦值．【解析】(1)因为AD=CD，E为AC的中点，所以AC⊥DE；在△ABD和△CBD中，因为AD=CD,∠ADB=∠CDB,DB=DB，所以△ABD≌△CBD，所以AB=CB，又因为E为AC的中点，所以AC⊥BE；又因...