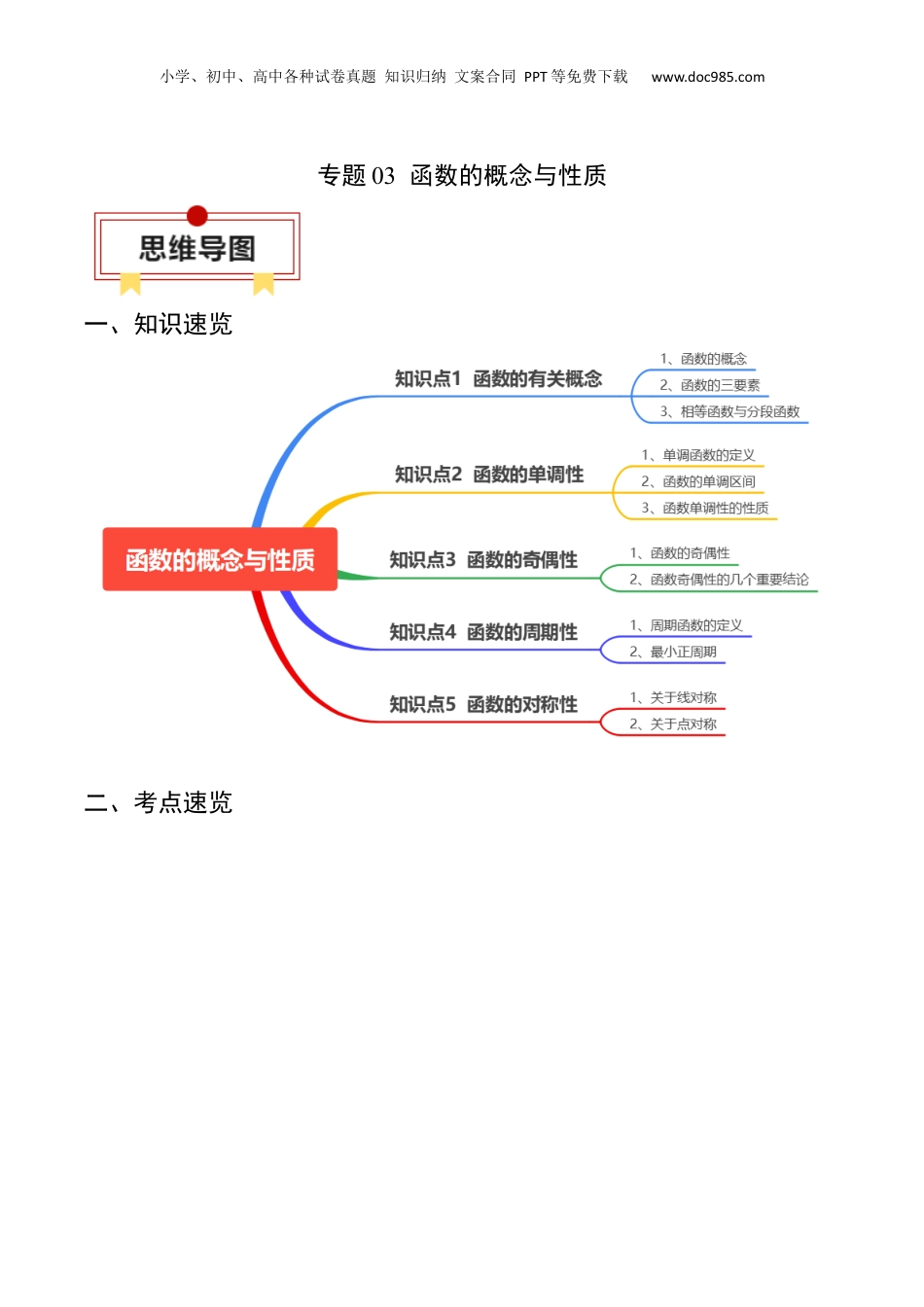
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题03函数的概念与性质一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1函数的有关概念1、函数的概念：一般地，设是非空的数集，如果对于集合中的任意一个数，按照某种确定的对应关系，在集合中都有唯一确定的和它对应，那么就称为从集合到集合的一个函数，记作.2、函数的三要素：（1）在函数中，叫做自变量，的取值范围叫做函数的定义域；（2）与的值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域。显然，值域是集合B的子集．（3）函数的对应关系：.3、相等函数与分段函数（1）相等函数：如果两个函数的定义域和对应关系完全一致，则这两个函数相等，这是判断两函数相等的依据．（2）分段函数：在函数定义域内，对于自变量取值的不同区间，有着不同的对应关系，这样的函数称为分段函数。分段函数的定义域是各段定义域的并集，值域是各段值域的并集。分段函数虽然是由几个部分构成，但它表示的是一个函数，各部分函数定义域不可以相交。知识点2函数的单调性小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、单调函数的定义设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2，当x1<x2时，都有f(x1)<f(x2)，那么就说函数f(x)在区间D上是单调递增函数。当x1<x2时，都有f(x1)>f(x2)，那么就说函数f(x)在区间D上是单调递减函数。单调性的图形趋势（从左往右）上升趋势下降趋势2、函数的单调区间若函数y＝f(x)在区间D上是增函数或减函数，则称函数y＝f(x)在这一区间上具有(严格的)单调性，区间D叫做y＝f(x)的单调区间．【注意】（1）函数单调性关注的是整个区间上的性质，单独一点不存在单调性问题，故单调区间的端点若属于定义域，则区间可开可闭，若区间端点不属于定义域则只能开．（2）单调区间D⊆定义域I.（3）遵循最简原则，单调区间应尽可能大；（4）单调区间之间可用“，”分开，不能用“∪”，可以用“和”来表示；3、函数单调性的性质若函数f(x)与g(x)在区间D上具有单调性，则在区间D上具有以下性质：（1）f(x)与f(x)+C（C为常数）具有相同的单调性.（2）f(x)与−f(x)的单调性相反.（3）当a>0时，af(x)与f(x)单调性相同；当a<0时，af(x)与f(x)单调性相反.（4）若f(x)≥0，则f(x)与√f(x)具有相同的单调性.（5）若f(x)恒为正值或恒为负值，则当a>0时，f(x)与af(x)具有相反的单调性；当a<0时，f(x)与af(x)具有相同的单调性.（6）f(x)与g(x)的和与差的单调性（相同区间上）:简记为：↗+↗=↗;（2）↘+↘=↘;（3）↗﹣↘=↗;（4）↘﹣↗=↘.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（7）复合函数的单调性：对于复合函数y＝f[g(x)]，若t＝g(x)在区间(a，b)上是单调函数，且y＝f(t)在区间(g(a)，g(b))或(g(b)，g(a))上是单调函数若t＝g(x)与y＝f(t)的单调性相同，则y＝f[g(x)]为增函数若t＝g(x)与y＝f(t)的单调性相反，则y＝f[g(x)]为减函数．简称“同增异减”．知识点3函数的奇偶性1、函数的奇偶性奇偶性定义图象特点偶函数如果对于函数的定义域内任意一个x，都有，那么函数f(x)是偶函数关于y轴对称奇函数如果对于函数f(x)的定义域内任意一个x，都有，那么函数是奇函数关于原点对称2、函数奇偶性的几个重要结论（1）为奇函数⇔的图象关于原点对称；为偶函数⇔的图象关于y轴对称．（2）如果函数是偶函数，那么．（3）既是奇函数又是偶函数的函数只有一种类型，即，x∈D，其中定义域D是关于原点对称的非空数集．（4）奇函数在两个对称的区间上具有相同的单调性，偶函数在两个对称的区间上具有相反的单调性．（5）偶函数在关于原点对称的区间上有相同的最大(小)值，取最值时的自变量互为相反数；奇函数在关于原点对称的区间上的最值互为相反数，取最值时的自变量也互为相反数．知识点4函数的周期性1、周期函数的定义对于函数，如果存在一个非零常数T，使得当x取定义域内的任何值时，都有，那么就称函数为周期函数，称T为这个函数的周期...