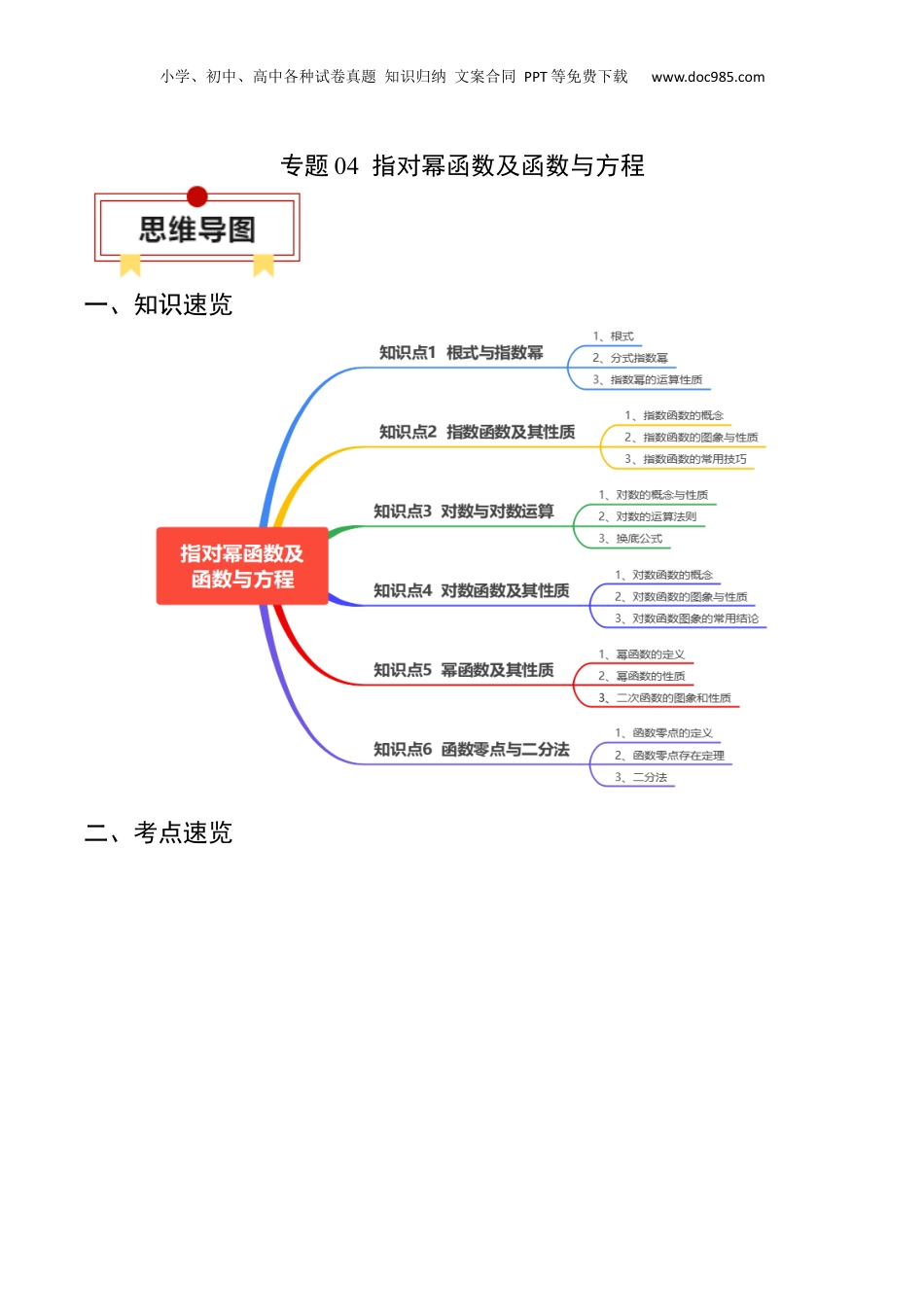
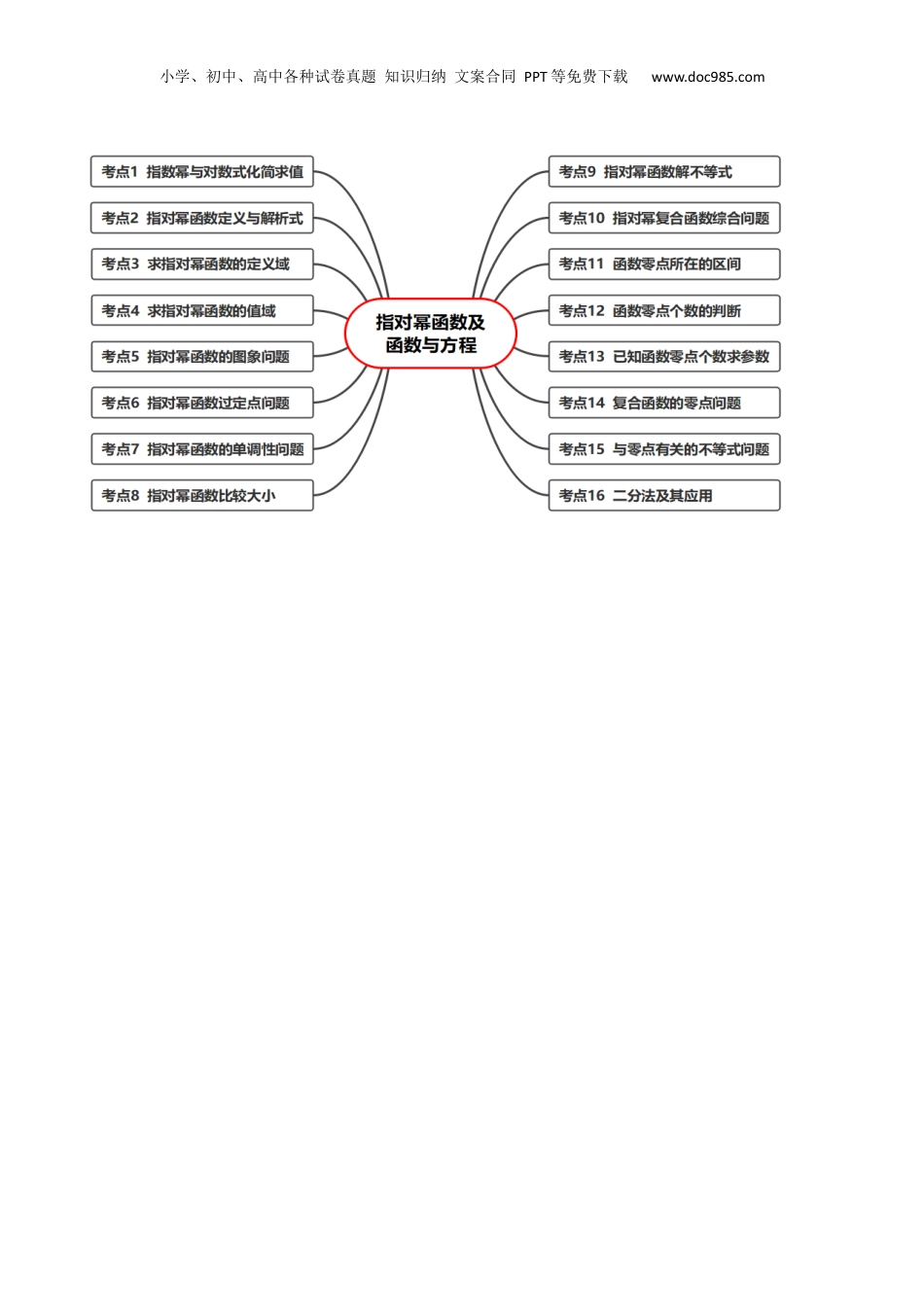
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题04指对幂函数及函数与方程一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1根式与指数幂1、根式（1）一般地，如果，那么x叫做a的n次方根，其中，且。式子叫做根式，这里n叫做根指数，a叫做被开方数．（2）的次方根的表示当n是奇数时，，的值仅有一个，记为当n是偶数，①时，的有两个值，且互为相反数，记为；②时，不存在（3）根式的性质（，且）：；2、分数指数幂（1）正分数指数幂：规定：（2）负分数指数幂：规定：（3）性质：0的正分数指数幂等于0，0的负分数指数幂没有意义3、指数幂的运算性质（1）无理数指数幂：一般地，无理数指数幂（，为无理数）是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．（2）指数幂的运算性质①．②．③．知识点2指数函数及其性质1、指数函数的概念一般地，函数（且）叫做指数函数，其中指数x是自变量，定义域是R，a是指数函数的底数．2、指数函数的图象与性质小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.coma>10<a<1图象图像特征在轴的上方，过定点当逐渐增大时，图象逐渐上升当逐渐增大时，图象逐渐下降性质定义域R值域(0,+∞)单调性在上是增函数在上是减函数奇偶性非奇非偶函数范围当时，；当时，；当时，；当时，；3、指数函数的常用技巧（1）当底数大小不定时，必须分“”和“”两种情况讨论；（2）指数函数的图象与底数大小的比较如图是指数函数（1）；（2）；（3）；（4）的图象，底数与1的之间的大小关系为；规律：在轴右（左）侧图象越高（低），其底数越大。（3）指数函数与的图象关于轴对称。知识点3对数与对数运算1、对数的概念与性质（1）对数的概念：如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底数N的对数，记作x＝logaN，其中a叫做对数的底数，N叫做真数，logaN叫做对数式。（2）对数的性质对数式与指数式的互化：ax＝N⇔x＝logaN(a>0，且a≠1)；①loga1＝0，②logaa＝1，③alogaN＝N，④logaaN＝N(a>0，且a≠1).指数式与对数式的关系小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2、对数的的运算法则如果a>0，且a≠1，M>0，N>0①loga(M·N)＝logaM＋logaN②loga＝logaM－logaN③logaMn＝nlogaM(n∈R)3、换底公式（1）logab＝(a>0，且a≠1，c>0，且c≠1，b>0)选用换底公式时，一般选用e或10作为底数。（2）换底公式的三个重要结论(1)logab＝；(2)logambn＝logab；(3)logab·logbc·logcd＝logad.知识点4对数函数及其性质1、对数函数的概念（1）定义：函数（，且）叫做对数函数，其中x是自变量，定义域为．（2）特殊的对数函数①常用对数函数：以10为底的对数函数y=lgx.②自然对数函数：以无理数e为底的对数函数y=lnx.2、对数函数的图象与性质图象a＞10＜a＜1性质定义域：(0，＋∞)值域：R当x＝1时，y＝0，即过定点(1,0)当0＜x＜1时，y＜0；当x＞1时，y＞0当0＜x＜1时，y＞0；当x＞1时，y＜0在(0，＋∞)上为增函数在(0，＋∞)上为减函数3、对数函数图象的常用结论（1）函数y＝logax与y=log1ax的图象x轴对称；（2）对数函数的图象与底数大小的关系如图，作直线y＝1，则该直线与四个函数图象交点的横坐标为相应的底数，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故0＜c＜d＜1＜a＜b.由此我们可得到以下规律：在第一象限内从左到右底数逐渐增大．知识点5幂函数及其性质1、幂函数的定义：一般地，函数y＝xα叫做幂函数，其中x是自变量，α是常数．（1）幂函数的特征：xα的系数是1；xα的底数x是自变量；xα的指数α为常数．只有满足这三个条件，才是幂函数．对于形如y＝(2x)α，y＝2x5，y＝xα＋6等的函数都不是幂函数．（2）幂函数的图象：同一坐标系中，幂函数y＝x，y＝x2，y＝x3，y＝x－1，y=x12的图象(如图)．2、幂函数的性质...