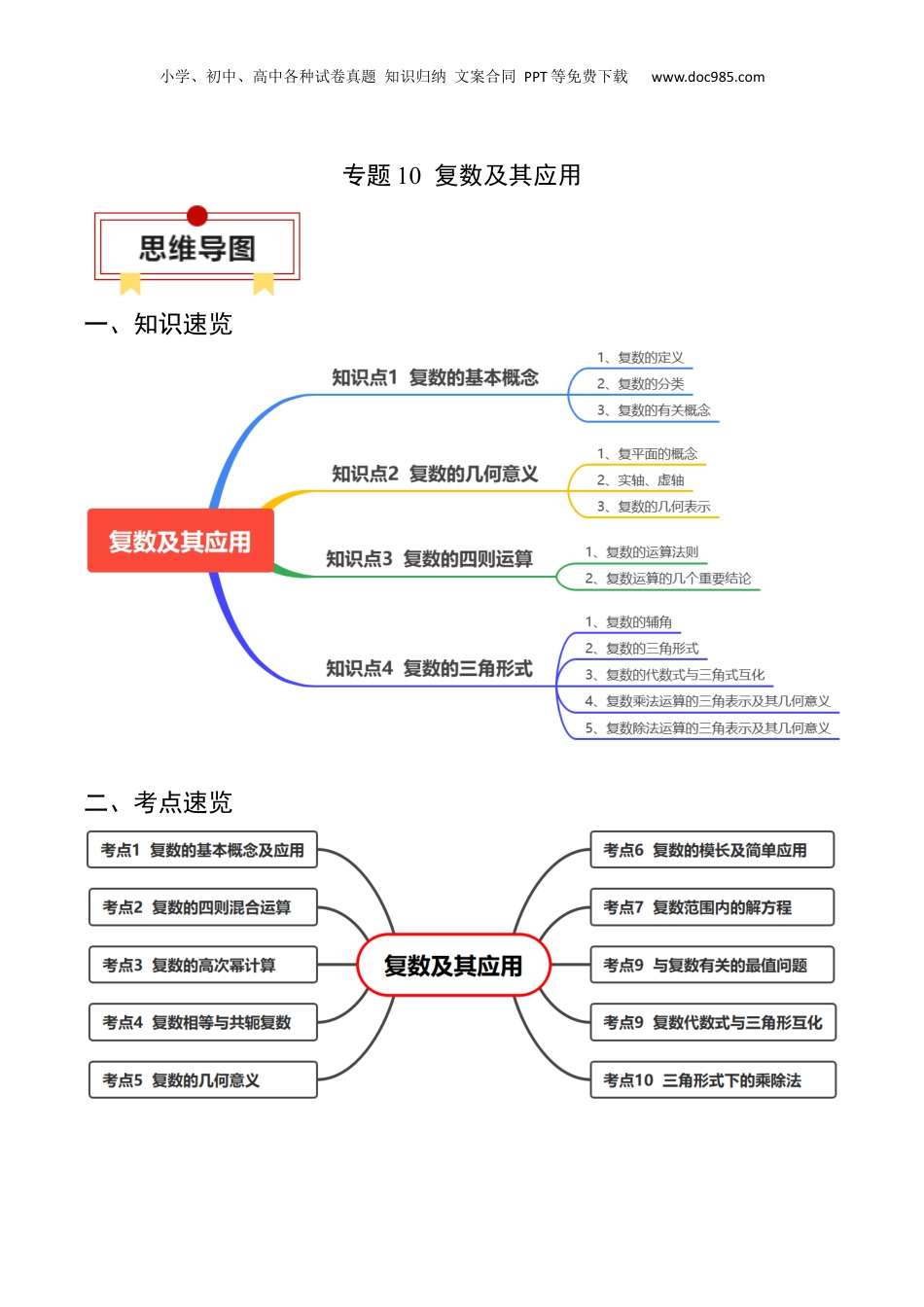
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题10复数及其应用一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1复数的基本概念1、复数的定义:形如a+bi(a,b∈R)的数叫做复数,其中实部是a,虚部是b.2、复数的分类:3、复数的有关概念复数相等a+bi=c+di⇔a=c且b=d(a,b,c,d∈R)共轭复数a+bi与c+di共轭⇔a=c且b=-d(a,b,c,d∈R)复数的模向量OZ―→的模叫做复数z=a+bi的模,记作|z|或|a+bi|,即|z|=|a+bi|=r=(r≥0,a,b∈R)知识点2复数的几何意义1、复平面的概念:建立直角坐标系来表示复数的平面叫做复平面;2、实轴、虚轴:在复平面内,x轴叫做实轴,y轴叫做虚轴,实轴上的点都表示实数;除原点以外,虚轴上的点都表示纯虚数;3、复数的几何表示:复数z=a+bi复平面内的点Z(a,b)平面向量知识点3复数的四则运算1、复数的运算法则设,(a,b,c,d∈R),则:(1)z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i;(2)z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i;(3)z1·z2=(a+bi)(c+di)=(ac-bd)+(ad+bc)i;(4)2、复数运算的几个重要结论(1)|z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2).(2)·z=|z|2=||2.(3)若z为虚数,则|z|2≠z2.(4)(1±i)2=±2i.(4)=i;=-i.(5)i4n=1;i4n+1=i;i4n+2=-1;i4n+3=-i.知识点4复数的三角形式小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、复数的辅角(1)辅角的定义:设复数z=a+bi的对应向量为⃗OZ,以x轴的非负半轴为始边,向量⃗OZ所在的射线(射线OZ)为终边的角θ,叫做复数z的辅角.(2)辅角的主值:根据辅角的定义及任意角的概念可知,任何一个不为零的复数辅角有无限多个值,且这些值相差2π的整数倍.规定:其中在0≤θ<2π范围内的辅角θ的值为辅角的主值,通常记作argz【注意】因为复数0对应零向量,而零向量的方向是任意的,所以复数0的辅角是任意的。2、复数的三角形式定义:任何一个复数都可以表示成z=r(cosθ+isinθ)的形式,其中r是复数的模,θ是复数的辅角.【注意】复数的三角形式必须满足:模非负,角相同,余正弦,加号连。3、复数的代数式与三角式互化将复数z=a+bi(a,b∈R)化为三角形式z=r(cosθ+isinθ)时,要注意以下两点:(1)r=❑√a2+b2,(2)cosθ=ar,sinθ=br,其中θ终边所在象限与点(a,b)所在象限相同,当a=0,b>0时,argz=π2【注意】每一个不等于零的复数有唯依的模与辅角的主值,并且由它的模与辅角的主值唯一确定。因此,两个非零复数相等当且仅当它们的模与辅角的主值分别相等。4、复数乘法运算的三角表示及其几何意义(1)复数乘法运算的三角表示:已知z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),则z1z1=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]这就是说,两个复数相乘,积的模等于各复数的模的积,积的辅角等于各复数的辅角的和。(2)复数乘法运算的几何意义:两个复数z1,z2相乘时,分别画出与z1,z2对应的向量⃗OZ1,⃗OZ2,然后把向量⃗OZ1绕O点按逆时针方向旋转θ2(如果θ2<0,就要把⃗OZ1绕点O按顺时针方向旋转角|θ2|),再把它的模变成原来的r2倍,得到向量⃗OZ,⃗OZ表示的复数就是积z1z2,这就是复数乘法的几何意义。(3)复数乘法运算三角表示推广:z1z2…zn=r1(cosθ1+isinθ1)∙r2(cosθ2+isinθ2)∙…∙rn(cosθn+isinθn)¿r1r2…rn[cos(θ1+θ2+…+θn)+isin(θ1+θ2+…+θn)]特别的,当z1=z2=…=zn=r(cosθ+isinθ)时,[r(cosθ+isinθ)]n=rn(cosnθ+isinnθ)5、复数除法运算的三角表示及其几何意义(1)复数除法运算的三角表示:已知z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则z1z2=r1(cosθ1+isinθ1)r2(cosθ2+isinθ2)=r1r2[cos(θ1−θ2)+isin(θ1−θ2)]这就是说,两个复数相除,商的模等于被除数的模除以除数的模所得的商,商的辅角等于被除数的辅角减去除数的辅角所得的差.(2)两个复数z1,z2相除时,先分别画出...