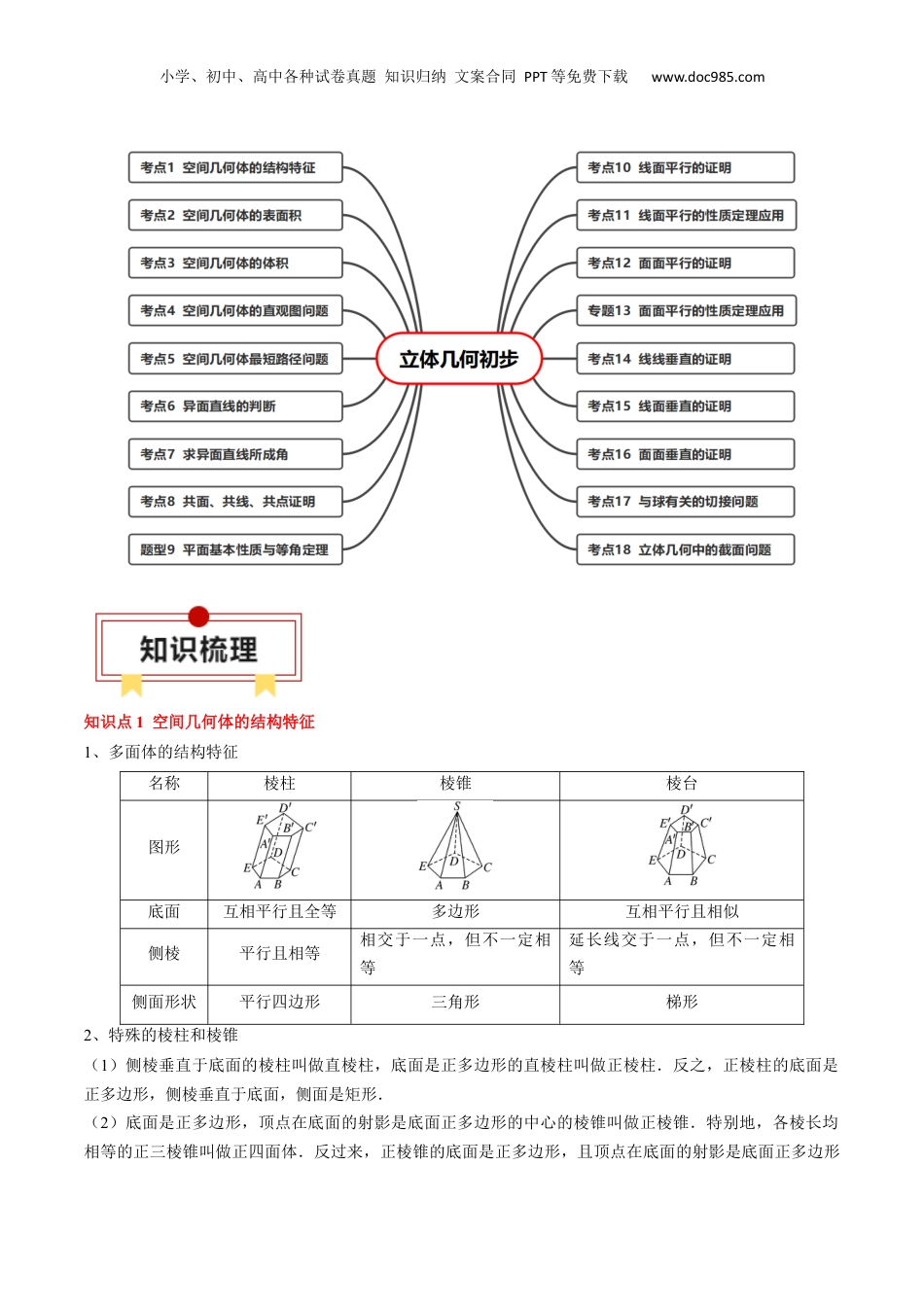
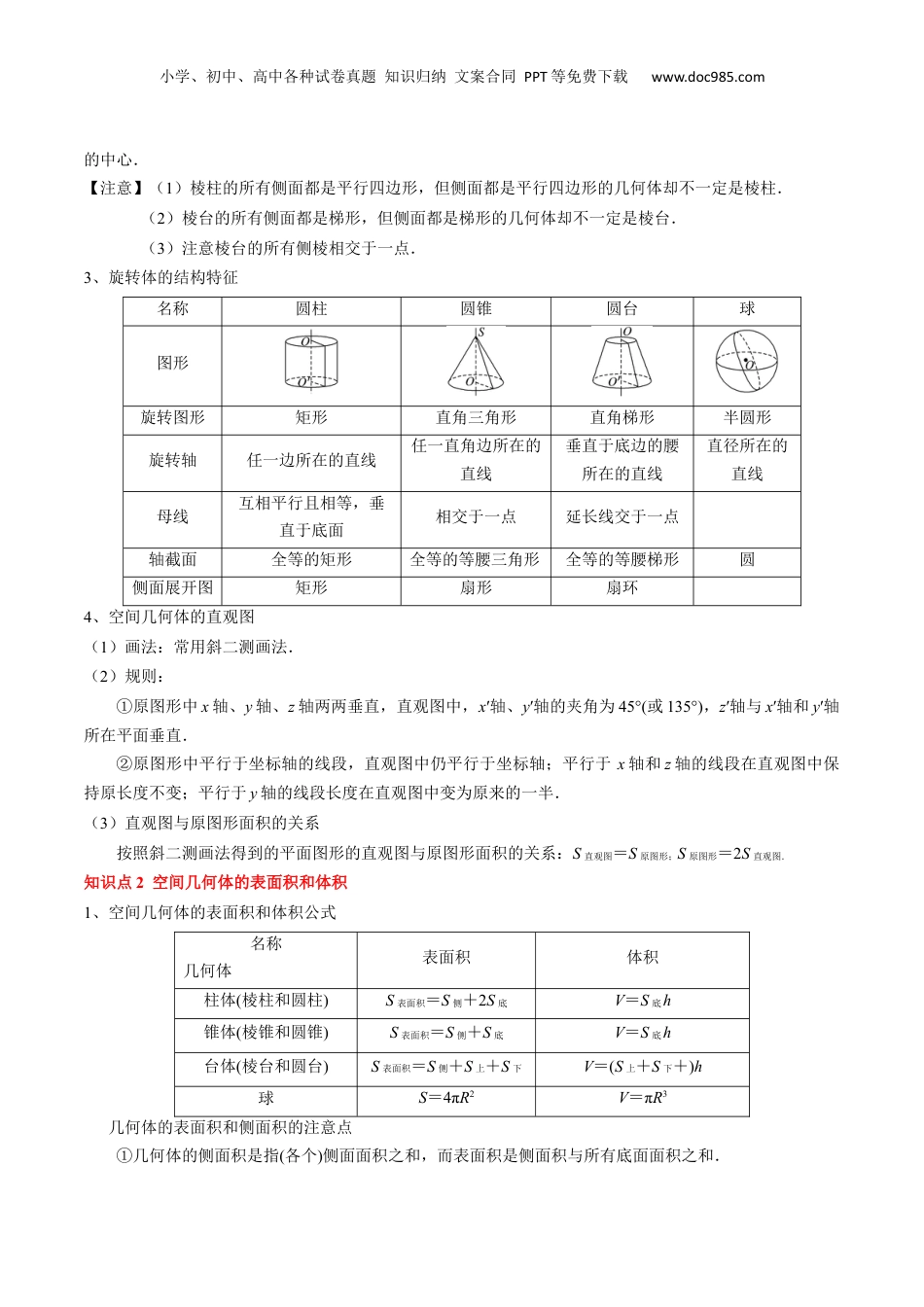
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题13立体几何初步一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1空间几何体的结构特征1、多面体的结构特征名称棱柱棱锥棱台图形底面互相平行且全等多边形互相平行且相似侧棱平行且相等相交于一点,但不一定相等延长线交于一点,但不一定相等侧面形状平行四边形三角形梯形2、特殊的棱柱和棱锥(1)侧棱垂直于底面的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱.反之,正棱柱的底面是正多边形,侧棱垂直于底面,侧面是矩形.(2)底面是正多边形,顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥.特别地,各棱长均相等的正三棱锥叫做正四面体.反过来,正棱锥的底面是正多边形,且顶点在底面的射影是底面正多边形小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com的中心.【注意】(1)棱柱的所有侧面都是平行四边形,但侧面都是平行四边形的几何体却不一定是棱柱.(2)棱台的所有侧面都是梯形,但侧面都是梯形的几何体却不一定是棱台.(3)注意棱台的所有侧棱相交于一点.3、旋转体的结构特征名称圆柱圆锥圆台球图形旋转图形矩形直角三角形直角梯形半圆形旋转轴任一边所在的直线任一直角边所在的直线垂直于底边的腰所在的直线直径所在的直线母线互相平行且相等,垂直于底面相交于一点延长线交于一点轴截面全等的矩形全等的等腰三角形全等的等腰梯形圆侧面展开图矩形扇形扇环4、空间几何体的直观图(1)画法:常用斜二测画法.(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴;平行于x轴和z轴的线段在直观图中保持原长度不变;平行于y轴的线段长度在直观图中变为原来的一半.(3)直观图与原图形面积的关系按照斜二测画法得到的平面图形的直观图与原图形面积的关系:S直观图=S原图形;S原图形=2S直观图.知识点2空间几何体的表面积和体积1、空间几何体的表面积和体积公式名称几何体表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=S底h锥体(棱锥和圆锥)S表面积=S侧+S底V=S底h台体(棱台和圆台)S表面积=S侧+S上+S下V=(S上+S下+)h球S=4πR2V=πR3几何体的表面积和侧面积的注意点①几何体的侧面积是指(各个)侧面面积之和,而表面积是侧面积与所有底面面积之和.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com②组合体的表面积应注意重合部分的处理.2、柱体、锥体、台体侧面积间的关系(1)当正棱台的上底面与下底面全等时,得到正棱柱;当正棱台的上底面缩为一个点时,得到正棱锥,则S正棱柱侧=ch′←――S正棱台侧=(c+c′)h′――→S正棱锥侧=ch′.(2)当圆台的上底面半径与下底面半径相等时,得到圆柱;当圆台的上底面半径为零时,得到圆锥,则S圆柱侧=2πrl←――S圆台侧=π(r+r′)l――→S圆锥侧=πrl.3、柱体、锥体、台体体积间的关系知识点3点、直线、平面之间的位置关系1、四个公理(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.作用:判断一条直线是否在某个平面内的依据(2)公理2:过不在一条直线上的三点,有且只有一个平面.【拓展】公理2的三个推论推论1:经过一条直线和这条直线外一点有且只有一个平面.推论2:经过两条相交直线有且只有一个平面.推论3:经过两条平行直线有且只有一个平面.作用:公理2及其推论是判断或证明点、线共面的依据(3)公理3:如果两个不重合的平面有一个公共点,则它们有且只有一条过该点的公共直线.作用:公理3是证明三线共点或三点共线的依据(4)公理4:平行于同一条直线的两条直线互相平行.2、等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.3、直线与直线的位置关系(1)空间两条直线的位置关系位置关系特点相交同一平面内,有且只有一个公共点平行同一平面内,没有公共点异面直线不同在任何一个平面内...