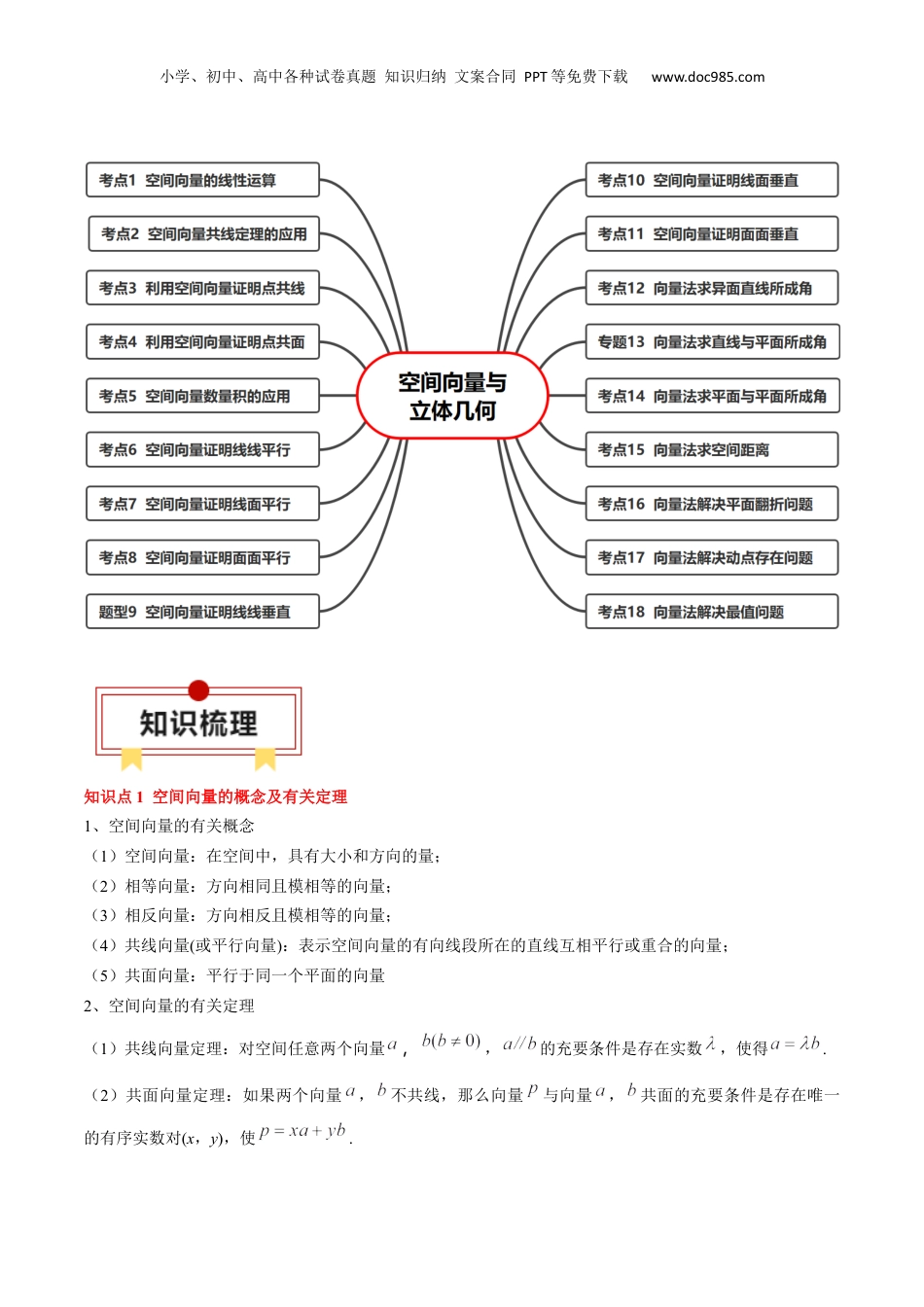
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题14空间向量与立体几何一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1空间向量的概念及有关定理1、空间向量的有关概念（1）空间向量：在空间中，具有大小和方向的量；（2）相等向量：方向相同且模相等的向量；（3）相反向量：方向相反且模相等的向量；（4）共线向量(或平行向量)：表示空间向量的有向线段所在的直线互相平行或重合的向量；（5）共面向量：平行于同一个平面的向量2、空间向量的有关定理（1）共线向量定理：对空间任意两个向量，，的充要条件是存在实数，使得.（2）共面向量定理：如果两个向量，不共线，那么向量与向量，共面的充要条件是存在唯一的有序实数对(x，y)，使.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（3）空间向量基本定理：如果三个向量，，不共面，那么对空间任一向量，存在有序实数组{x，y，z}，使得，其中，叫做空间的一个基底．知识点2两个向量的数量积及其运算1、空间向量的数量积及运算律（1）数量积及相关概念①两向量的夹角：已知两个非零向量，，在空间任取一点O，作，，则∠AOB叫做向量与的夹角，记作，其范围是[0，π]，若，则称与互相垂直，记作.②非零向量，的数量积．（2）空间向量数量积的运算律①结合律：；②交换律：；③分配律：.2、空间向量的坐标表示及其应用设123(,,)aaaa，123(,,)bbbb，向量表示坐标表示数量积共线，，垂直模夹角知识点3空间中的平行与垂直的向量表示1、直线的方向向量和平面的法向量（1）直线的方向向量：如果表示非零向量的有向线段所在直线与直线l平行或重合，则称此向量为直线l的方向向量．（2）平面的法向量：直线l⊥α，取直线l的方向向量，则向量叫做平面α的法向量．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2、空间位置关系的向量表示位置关系向量表示直线l1，l2的方向向量分别为，直线l的方向向量为，平面α的法向量为平面α，β的法向量分别为，知识点4利用空间向量求空间角1、异面直线所成角设异面直线a，b所成的角为θ，则，其中，分别是直线a，b的方向向量．2、直线与平面所成角如图所示，设l为平面α的斜线，l∩α＝A，为l的方向向量，为平面α的法向量，φ为l与α所成的角，则.3、二面角（1）若AB，CD分别是二面角αlβ的两个平面内与棱l垂直的异面直线，则二面角(或其补角)的大小就是向量与的夹角，如图a.（2）平面α与β相交于直线l，平面α的法向量为，平面β的法向量为，，则二面角αl-β为θ或π－θ.设二面角大小为φ，则，如图b，c.知识点5利用空间向量求空间距离1、点到直线的距离已知直线l的单位方向向量为u，A是直线l上的定点，P是直线l外一点，设向量AP在直线l上的投影向量为AQ＝a，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则点P到直线l的距离为(如图)．2、点到平面的距离已知平面的法向量为,是平面内的任一点，是平面外一点，过点作则平面的垂线，交平面于点，则点到平面的距离为（如图）.3、线面距和面面距线面距、面面距均可转化为点面距离，用求点面距的方法进行求解。（1）直线a与平面之间的距离：||ABndn，其中,AaB，n是平面的法向量。（2）两平行平面,之间的距离：||ABndn，其中,AB，n是平面的法向量。一、用基向量表示指定向量的方法（1）结合已知向量和所求向量观察图形．（2）将已知向量和所求向量转化到三角形或平行四边形中．（3）利用三角形法则或平行四边形法则把所求向量用已知基向量表示出来．【典例1】（2023·全国·高三对口高考）如图所示，在平行六面体中，为与的交点，若，，则（）A．B．C．D．【答案】D【解析】由题意可得：.故选：D.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【典例2】（2021·全国·高三专题练习）在四面体中，，点在棱上，且，为中点，则（）A．B．C．D．【答案】B【解析】点在线段上，且，为中点，...