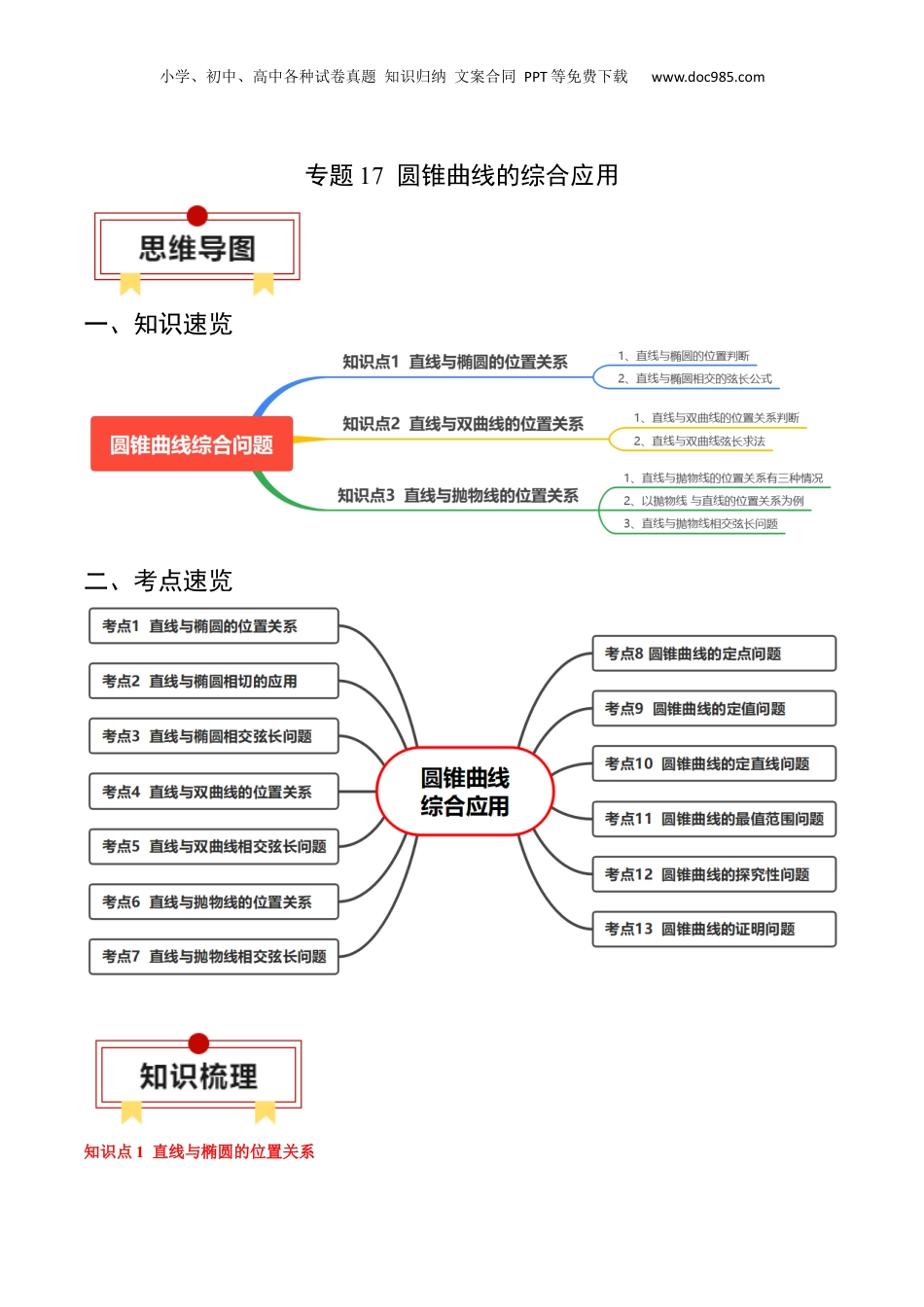
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题17圆锥曲线的综合应用一、知识速览二、考点速览知识点1直线与椭圆的位置关系小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、直线与椭圆的位置判断设直线方程为，椭圆方程为联立消去y得一个关于x的一元二次方程①直线和椭圆相交直线和椭圆有两个交点(或两个公共点）；②直线和椭圆相切直线和椭圆有一个切点(或一个公共点)；③直线和椭圆相离直线和椭圆无公共点．2、直线与椭圆相交的弦长公式（1）定义：连接椭圆上两个点的线段称为椭圆的弦．（2）求弦长的方法①交点法：将直线的方程与椭圆的方程联立，求出两交点的坐标，然后运用两点间的距离公式来求．②根与系数的关系法：如果直线的斜率为k，被椭圆截得弦AB两端点坐标分别为(x1，y1)，(x2，y2)，则弦长公式为：知识点2直线与双曲线的位置关系1、直线与双曲线的位置关系判断将双曲线方程与直线方程联立消去得到关于的一元二次方程，（1）当，即，直线与双曲线的渐近线平行，直线与双曲线只有一个交点；（2）当，即，设该一元二次方程的判别式为，若，直线与双曲线相交，有两个公共点；若，直线与双曲线相切，有一个公共点；若，直线与双曲线相离，没有公共点；注意：直线与双曲线有一个公共点时，可能相交或相切.2、直线与双曲线弦长求法若直线与双曲线（，）交于，两点，则或（）．（具体同椭圆相同）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点3直线与抛物线的位置关系1、直线与抛物线的位置关系有三种情况相交（有两个公共点或一个公共点）；相切（有一个公共点）；相离（没有公共点）.2、以抛物线与直线的位置关系为例：（1）直线的斜率不存在，设直线方程为，若，直线与抛物线有两个交点；若，直线与抛物线有一个交点，且交点既是原点又是切点；若，直线与抛物线没有交点.（2）直线的斜率存在.设直线，抛物线，直线与抛物线的交点的个数等于方程组，的解的个数，即二次方程（或）解的个数.①若，则当时，直线与抛物线相交，有两个公共点；当时，直线与抛物线相切，有个公共点；当时，直线与抛物线相离，无公共点.②若，则直线与抛物线相交，有一个公共点.3、直线与抛物线相交弦长问题（1）一般弦长设为抛物线的弦，，，弦AB的中点为.①弦长公式：（为直线的斜率，且）.②,推导：由题意，知，①②由①-②，得，故，即.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com③直线的方程为.（2）焦点弦长如图，是抛物线过焦点的一条弦，设，，的中点，过点，，分别向抛物线的准线作垂线，垂足分别为点，，，根据抛物线的定义有，，故.又因为是梯形的中位线，所以，从而有下列结论；①以为直径的圆必与准线相切.②(焦点弦长与中点关系)③.④若直线的倾斜角为，则.⑤，两点的横坐标之积，纵坐标之积均为定值，即，.⑥为定值.一、直线与圆锥曲线位置关系1、直线与圆锥曲线有两个不同的公共点的判定：通常的方法是直线与圆锥曲线方程联立方程消元后得到一元二次方程，其中；另一方面就是数形结合，如直线与双曲线有两个不同的公共点，可通过判定直线的斜率与双曲线渐近线的斜率的大小得到．2、直线与圆锥曲线只有一个公共点则直线与双曲线的一条渐近线平行，或直线与抛物线的对称轴平行，或直线与圆锥曲线相切．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【典例1】（2023·全国·高三专题练习）直线l：与椭圆C：的位置关系是（）A．相交B．相切C．相离D．不能确定【典例2】（2023·高三课时练习）直线与抛物线的位置关系为（）A．相交B．相切C．相离D．不能确定【典例3】（2023·四川成都·高三模拟预测）已知命题p：，命题q：直线与抛物线有两个公共点，则p是q的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【典例4】（2023上·江西南昌·高三校考阶段练习）已知直线与双曲线，若直线与双曲线左支交于两点，求实数的取值范围.二、直线与圆锥曲线的弦长问题设，根据两点距离公式．（1）若在直...