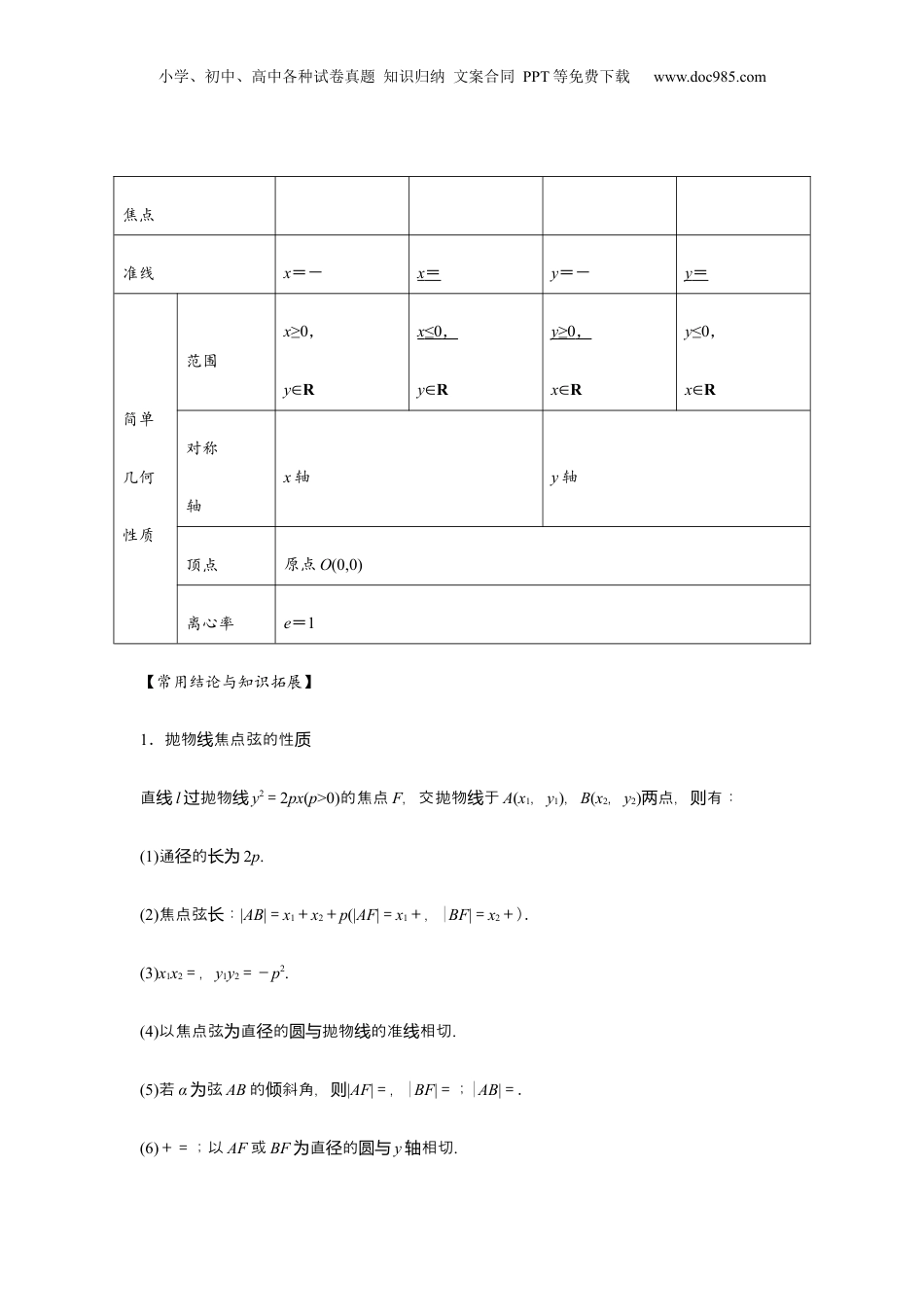
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题8.6抛物线目录题型一：抛物线的定义................................................................................................................4题型二：抛物线的标准方程.........................................................................................................5题型三：抛物线的焦点弦............................................................................................................7题型四：最值问题........................................................................................................................8题型五：抛物线与直线方程.........................................................................................................9题型六：弦长、面积问题...........................................................................................................11知识点一、抛物线的定义我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点，直线l叫做抛物线的准线.知识点二、抛物线标准方程和简单几何性质标准方程y2＝2px(p＞0)y2＝－2px(p＞0)x2＝2py(p＞0)x2＝－2py(p＞0)图形开口向右向左向上向下知识点总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com焦点准线x＝－x＝y＝－y＝简单几何性质范围x≥0，y∈Rx≤0，y∈Ry≥0，x∈Ry≤0，x∈R对称轴x轴y轴顶点原点O(0,0)离心率e＝1【常用结论与知识拓展】1．抛物焦点弦的性线质直线l抛物过线y2＝2px(p>0)的焦点F，交抛物于线A(x1，y1)，B(x2，y2)点，有：两则(1)通的径长为2p.(2)焦点弦：长|AB|＝x1＋x2＋p(|AF|＝x1＋，|BF|＝x2＋).(3)x1x2＝，y1y2＝－p2.(4)以焦点弦直的抛物的准相切为径圆与线线.(5)若α弦为AB的斜角，倾则|AF|＝，|BF|＝；|AB|＝.(6)＋＝；以AF或BF直的为径圆与y相切轴.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．抛物中的最线值P抛物为线y2＝2px(p>0)上的任一点，F焦点，有：为则|PF|≥；焦点弦AB以通径(2p)最为小；值A(m，n)一定点，为则|PA|＋|PF|有最小值.3．抛物的切线线已知抛物线C：x2＝2py(p>0)的焦点为F，焦点经过F的直线l抛物相交于与线A，B点，两分别过A，B作抛物线C的切两条线l1，l2，l1∩l2＝P.有：则(1)l1⊥l2；(2)P在定直线x＝－上；(3)PF⊥AB．4．抛物中的焦点三角形线如右，抛物图过线y2＝2px(p>0)的焦点F的直线l：y＝kx－(其中k直为线l的斜率)交抛物于线A，B点，那焦点三角形两么OAB的面可以表示积为S△OAB＝(若抛物方程线为x2＝2py(p>0)，直线l：y＝kx＋，则S△OAB＝)．题型一：抛物线的定义【要点讲解】以抛物线为背景的点的轨迹问题求解策略：借助题目给出的“几何特征”判断平面内动点所满足的“几何条件”，根据抛物线定义即可得出结果．与抛物线上一点有关的距离的最值问题，往往根据抛物线的定义，将到焦点的距离和到准线距离相互转化，再根据“共线”的几何特征进行求解．例题精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例1】若点到点的距离比它到直线的距离大1，则点的轨迹方程为A．B．C．D．【变式训练1】已知点为抛物线上的点，且点到抛物线的焦点的距离为3，则．【变式训练2】动点到点的距离比它到直线的距离大1，则动点的轨迹是A．椭圆B．双曲线C．双曲线的一支D．抛物线【变式训练3】设抛物线的焦点为，经过点的直线与抛物线相交于、两点，若点恰为线段的中点，则．【变式训练4】已知曲线上的任意一点到定点的距离与到定直线的距离相等．（Ⅰ）求曲线的方程；（Ⅱ）若曲线上有两个定点、分别在其对称轴的上、下两侧，且，，求原点到直线的距离．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型二：抛物线的标准方程【要点讲解】求抛物线标准方程的常用方法是待定系数法，其关键是判断焦点位置、开口方...