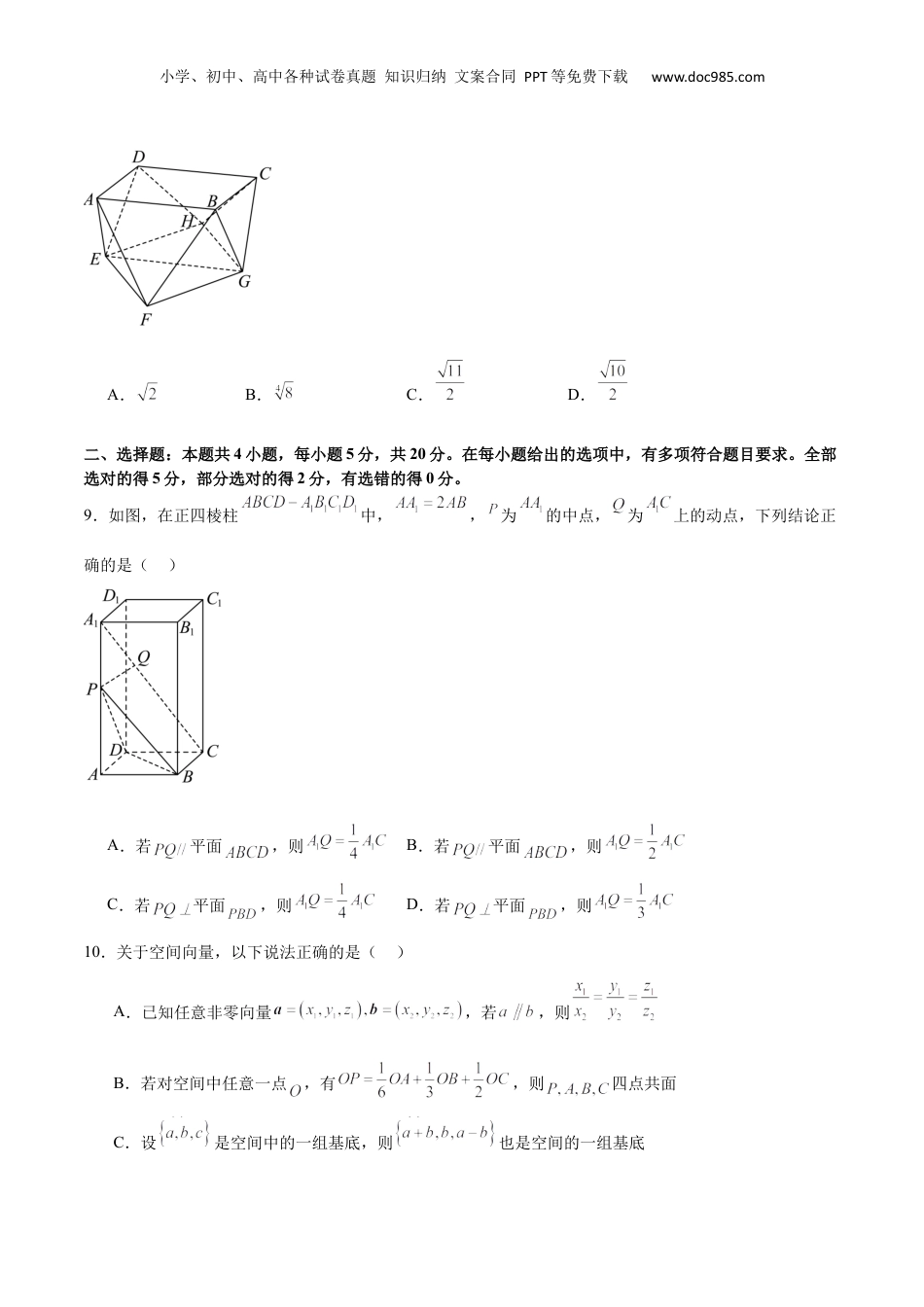
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com模块六立体几何（测试）（考试时间：120分钟试卷满分：150分）第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。1．在四面体中，，则四面体外接球的体积为（）A．B．C．D．2．如图所示，在正方体中，E为线段上的动点，则下列直线中与直线CE夹角为定值的直线为（）A．直线B．直线C．直线D．直线3．若平面截球所得截面圆的面积为，且球心到平面的距离为，则球的表面积为（）A．B．C．D．4．在三棱柱中，平面是等边三角形，是棱的中点，在棱上，且.若，则异面直线与所成角的余弦值是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．5．《几何原本》是古希腊数学家欧几里得的一部不朽之作，书中称轴截面为等腰直角三角形的圆锥为直角圆锥，若直角圆锥底面圆的半径为1，则其内接正方体的棱长为（）A．B．C．D．6．阿基米德多面体是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到的阿基米德多面体，如图所示.则该多面体所在正方体的外接球表面积为（）A．B．C．D．7．甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为，两圆锥的表面积分别为和，内切球半径分别为和．若，则的值是（）A．B．C．D．8．半正多面体是由边数不全相同的正多边形为面的多面体，如图所示的多面体就是一个半正多面体，其中四边形和四边形均为正方形，其余八个面为等边三角形，已知该多面体的所有棱长均为2，则平面与平面之间的距离为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．二、选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。9．如图，在正四棱柱中，，为的中点，为上的动点，下列结论正确的是（）A．若平面，则B．若平面，则C．若平面，则D．若平面，则10．关于空间向量，以下说法正确的是（）A．已知任意非零向量，若，则B．若对空间中任意一点，有，则四点共面C．设是空间中的一组基底，则也是空间的一组基底小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comD．若空间四个点，则三点共线11．在等腰梯形中，，点分别为的中点，以所在直线为旋转轴，将梯形旋转得到一旋转体，则（）A．该旋转体的侧面积为B．该旋转体的体积为C．直线与旋转体的上底面所成角的正切值为D．该旋转体的外接球的表面积为12．如图1，矩形由正方形与拼接而成．现将图形沿对折成直二面角，如图2．点（不与重合）是线段上的一个动点，点在线段上，点在线段上，且满足，，则（）图1图2A．B．C．的最大值为D．多面体的体积为定值第Ⅱ卷三、填空题：本题共4小题，每小题5分，共20分。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com13．一个正四棱台的下底面周长与上底面周长之差为16，且其侧面梯形的高为，则该正四棱台的高为.14．如图，四边形是平行四边形，是平面外一点，为上一点，若平面，则．15．在四棱锥中，底面是正方形，底面.若四棱锥的体积为9，且其顶点均在球上，则当球的体积取得最小值时，.16．刻画空间的弯曲性是几何研究的重要内容，在数学上用曲率刻画空间弯曲性.规定：多面体的顶点的曲率等于与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和.例如：正四面体在每个顶点有3个面角，每个面角是，所以正四面体在每个顶点的曲率为，故其总曲率为.根据曲率的定义，正方体在每个顶点的曲率为，四棱锥的总曲率为.四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步棸。17．（10分）如图，在直三棱柱中，分别为的中点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求异面直...