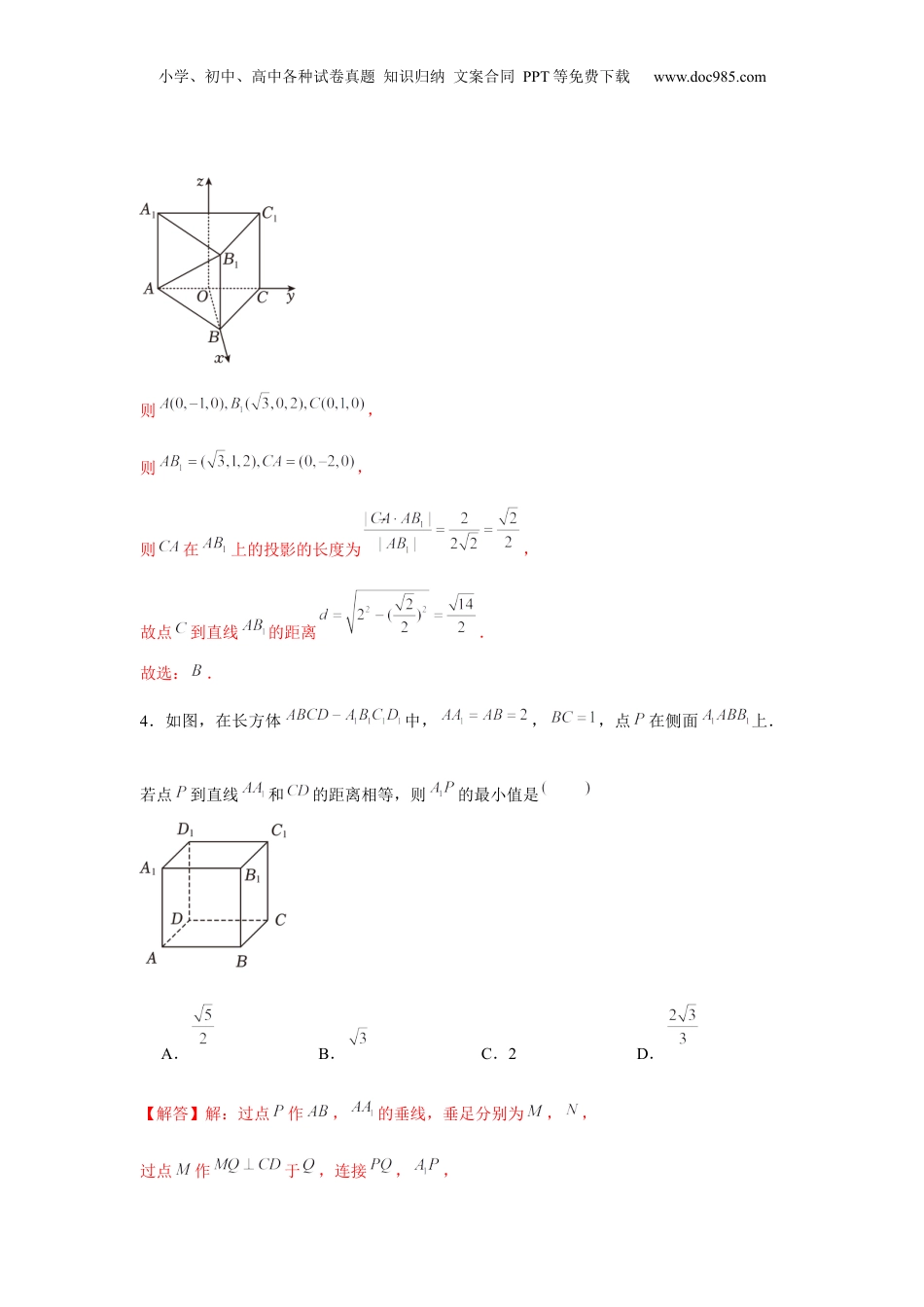
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com跟踪训练06向量法求空间角和距离一．选择题（共15小题）1．已知，2，、，4，、，2，，则原点到平面的距离是A．B．C．2D．【解答】解：由已知可得，，设平面的法向量为，则取，则平面的一个法向量为，而，所以原点到平面的距离．故选：．2．在长方体中，，，为的中点，则点到平面的距离为A．B．C．D．【解答】解：如图所示，以为坐标原点，以，，所在直线分别为，，轴建立空间直角坐标系，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，0，，，0，，，4，，，4，，则，，设，，是平面的一个法向量，则，令，则，又，所以点到平面的距离为．故选：．3．如图，在正三棱柱中，若，则点到直线的距离为A．B．C．D．【解答】解：取的中点，为等边三角形，则，以为原点，的方向分别为，轴的正方向建立空间直角坐标系，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则，则，则在上的投影的长度为，故点到直线的距离．故选：．4．如图，在长方体中，，，点在侧面上．若点到直线和的距离相等，则的最小值是A．B．C．2D．【解答】解：过点作，的垂线，垂足分别为，，过点作于，连接，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com因为，面面，面面，面，所以面，又面，所以，又，，所以面，又面，所以，在平面上，以，为坐标轴建立平面直角坐标系，设，，则，，所以，若点到直线和得距离相等，则，即，所以，所以当，时，取得最小值为．故选：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．空间中有三点，，，，，，，，，则点到直线的距离为A．B．C．3D．【解答】解：间中有三点，，，，，，，，，，1，，的一个单位方向向量为，1，，，，，，，点到直线的距离为．故选：．6．如图，在正方体中，截面与底面所成锐二面角的正切值为小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【解答】解：如图所示，连接交于点，连接，则，，为二面角的平面角，设，则，所以．故选：．7．已知直线，且向量是直线的一个方向向量，则实数的值为A．B．1C．2D．或2【解答】解：向量是直线的一个方向向量，直线的斜率，，解得：或．故选：．8．如图，在三棱柱中，，，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，与的交点为，则A．B．C．D．【解答】解：由题意得，，，，，．故选：．9．直线的方向向量为A．B．C．D．【解答】解：根据直线方程，可得直线的斜率为，所以直线的一个方向向量为，又，，，所以也是直线的一个方向向量．故选：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com10．我国古代数学名著《九章算术》对立体几何问题有着深入的研究，从其中的一些数学用语可见．譬如“堑堵”指底面为直角三角形且侧棱垂直于底面的三棱柱，“阳马”指底面是矩形且有一侧棱垂直于底面的四棱锥，“鳖臑”指四个面都是直角三角形的三棱锥．现有一如图所示的“堑堵”，其中，若，则到平面的距离为A．B．C．D．【解答】解：以为坐标原点，，，所在直线分别为，，轴，建立如图所示的空间直角坐标系，则，4，，，0，，，4，，，0，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，4，，，0，，，4，，设平面的法向量为，，，则，即，令，则，，所以，0，，所以到平面的距离为．故选：．11．如图，一块矿石晶体的形状为四棱柱，底面是正方形，，，且．则向量的模长为A．B．34C．52D．【解答】解：设，则，所以．故选：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com12．如图所示，在棱长为2的正方体中，点在棱上，且，则点，到平面的距离之和为A．B．C．D．【解答】解：在棱长为2的正方体中，平面，平面，则，由，得，在△中，，则，即点为中点，又因为，平面，平面，因此平面，于是点到平面的距离等于点到平面的距离，同理点到平面的距离...