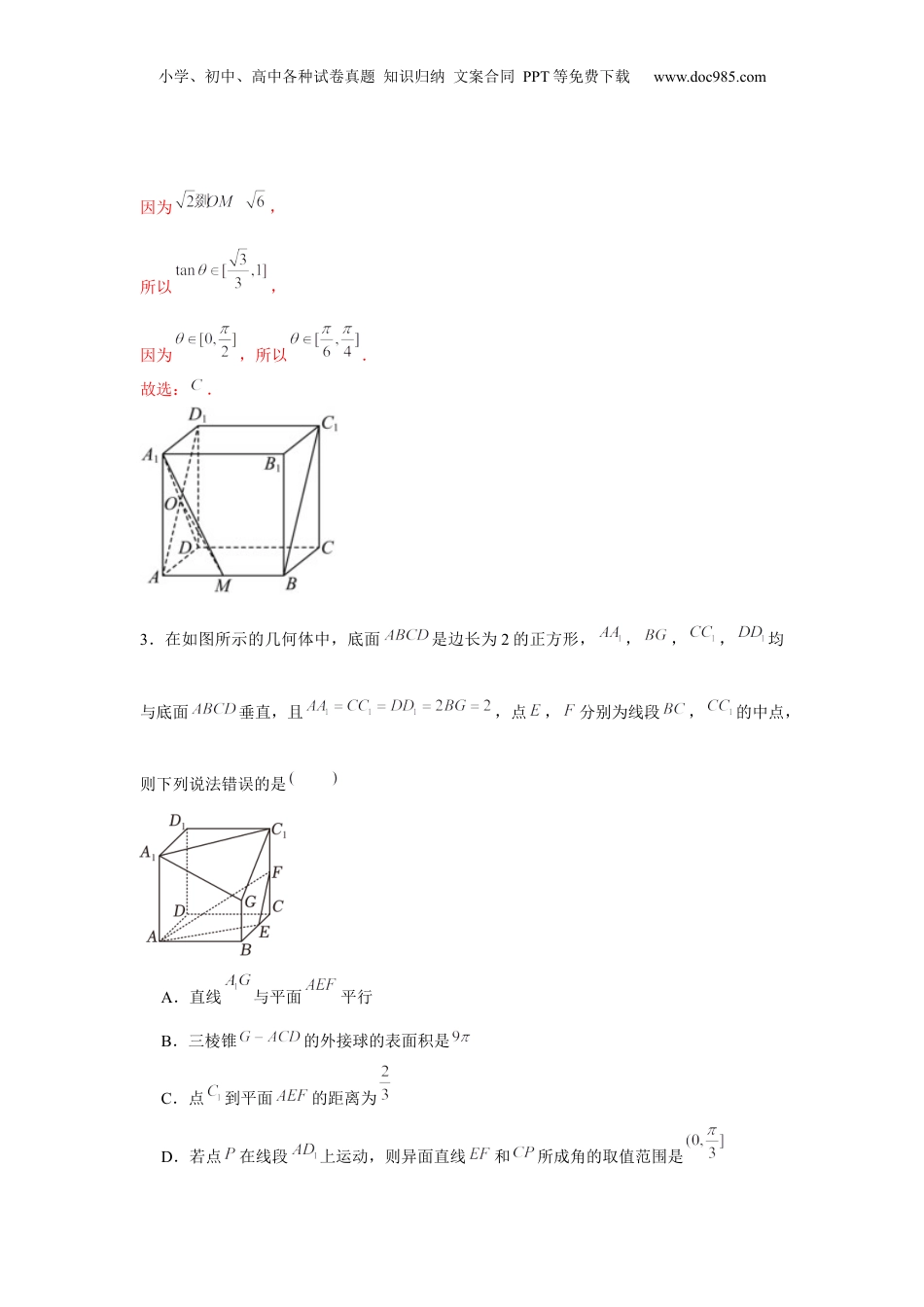
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点突破05立体几何中最值、范围问题一．选择题（共5小题）1．已知二面角的平面角为，与平面所成角为．记的面积为，的面积为，则的取值范围为A．B．C．D．【解答】解：作，垂足为，连接，，即，，，平面，平面，平面，，又，故平面，平面，为在内的射影，则为与平面所成角，即，，，为二面角的平面角，即，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在中，由正弦定理有：，，，又，，，又，，即，．故选：．2．在正方体中，点为棱上的动点，则与平面所成角的取值范围为A．B．C．D．【解答】解：设，连接，则，因为在正方体中，平面，平面，所以，因为，，平面，所以平面，所以即为与平面所成角．设，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com因为，所以，因为，所以．故选：．3．在如图所示的几何体中，底面是边长为2的正方形，，，，均与底面垂直，且，点，分别为线段，的中点，则下列说法错误的是A．直线与平面平行B．三棱锥的外接球的表面积是C．点到平面的距离为D．若点在线段上运动，则异面直线和所成角的取值范围是小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解答】解：如图建立空间直角坐标系，可得，0，，，2，，，2，，，0，，，0，，，2，，，2，，，0，，，2，，，2，，对于，2，，设平面的法向量，，，，2，，，2，，所以，令，得，，所以，1，，所以，2，，1，，所以直线与平面平行，选项正确；对于：三棱锥的外接球的球心为，，，则，所以，解得，，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以三棱锥的外接球的体积为，选项正确；对于，，，，所以，所以，，所以，所以，所以，所以，所以点到平面的距离为，选项正确；对于：设，0，，，，，，0，，所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，，所以异面直线和所成角的取值范围是，．选项错误．故选：．4．在正方体中，棱长为2，平面经过点，且满足直线与平面所成角为，过点作平面的垂线，垂足为，则长度的取值范围为A．B．C．D．【解答】解：如图所示，连接，因为，所以，又因为直线与平面所成角为，即，所以，所以在如图所示的圆锥底面上，所以，易知，，，所以，所以，．故选：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．在长方体中，，，是的中点，点在线段上（包含端点），若直线与平面所成的角为，则的取值范围是A．B．C．D．【解答】解：以为原点，分别以，，所在直线为，，轴，建立空间直角坐标系，如图所示，则，0，，，0，，，2，，，1，，，2，，设，则，，，则，，，，，设平面的法向量为，，，则，令，得，，所以，所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com由于，所以，所以．故选：．二．解答题（共10小题）6．如图4，在三棱台中，底面是边长为2的正三角形，侧面为等腰梯形，且，为的中点．（1）证明：；（2）记二面角的大小为，时，求直线与平面所成角的正弦值的取值范围．【解答】（1）证明：如图，作的中点，连接，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在等腰梯形中，，为，的中点，，在正中，为的中点，，，，，，平面，平面，又平面，．（2）解：平面，在平面内作，以为坐标原点，以，，，分别为，，，轴正向，如图建立空间直角坐标系，，，为二面角的平面角，即，，0，，，，0，，，，，设平面的法向量为，，，则有，，即，可得令，，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com即，，，又，，，，．7．如图，在三棱柱中，底面是边长为2的等边三角形，，，分别是线段，的中点，在平面内的射影为．（1）求证：平面；（2）若点为棱的中点，求点到平面的距离；（3）若点为线段上的动点（不包括端点），求锐二面角的余弦值的取值范围．小学、初中、高中各种试卷真题知识归纳文案合...