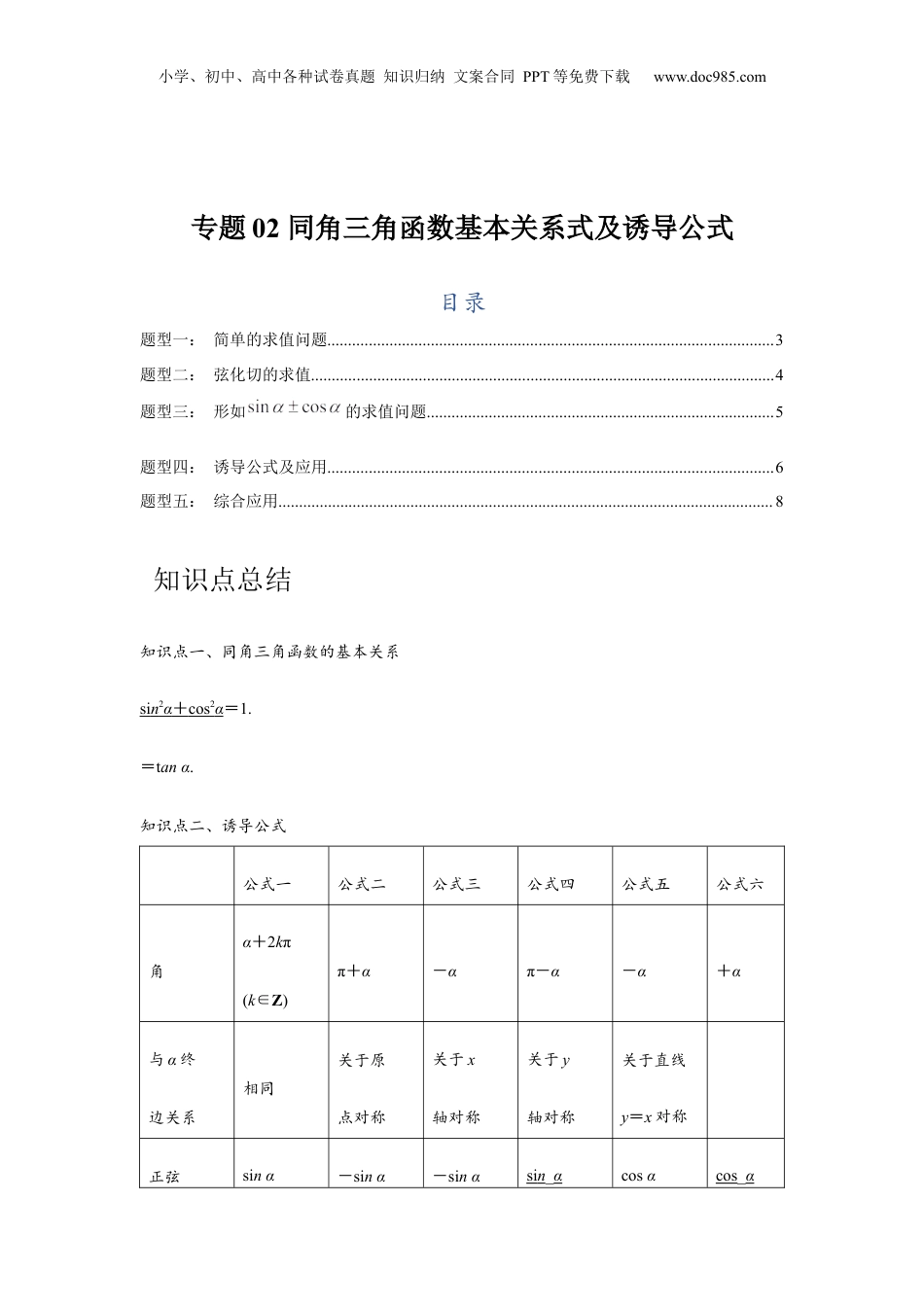
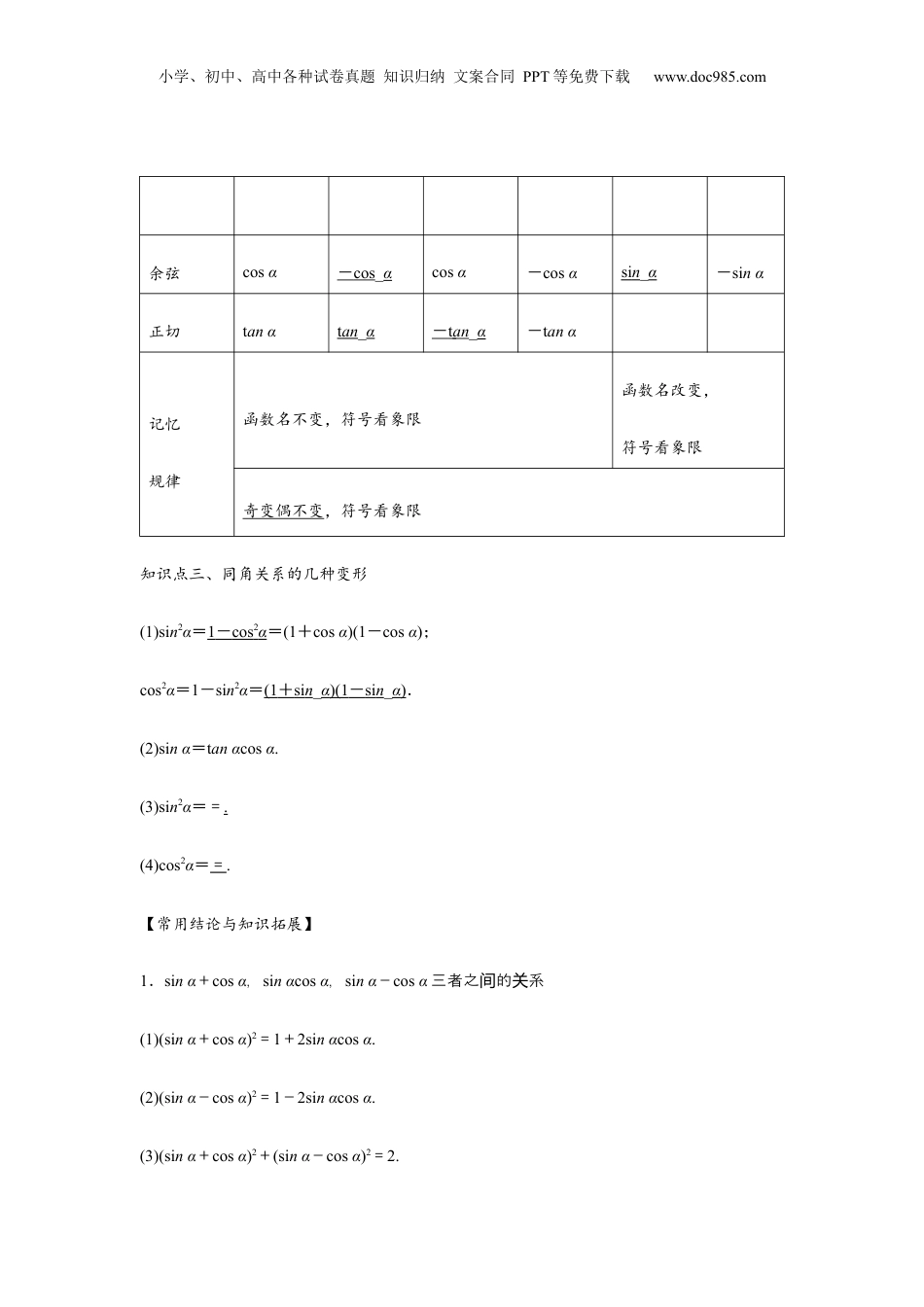
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题02同角三角函数基本关系式及诱导公式目录题型一：简单的求值问题............................................................................................................3题型二：弦化切的求值................................................................................................................4题型三：形如的求值问题....................................................................................5题型四：诱导公式及应用............................................................................................................6题型五：综合应用........................................................................................................................8知识点一、同角三角函数的基本关系sin2α＋cos2α＝1.＝tanα.知识点二、诱导公式公式一公式二公式三公式四公式五公式六角α＋2kπ(k∈Z)π＋α－απ－α－α＋α与α终边关系相同关于原点对称关于x轴对称关于y轴对称关于直线y＝x对称正弦sinα－sinα－sinαsin_αcosαcos_α知识点总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com余弦cosα－cos_αcosα－cosαsin_α－sinα正切tanαtan_α－tan_α－tanα记忆规律函数名不变，符号看象限函数名改变，符号看象限奇变偶不变，符号看象限知识点三、同角关系的几种变形(1)sin2α＝1－cos2α＝(1＋cosα)(1－cosα)；cos2α＝1－sin2α＝(1＋sin_α)(1－sin_α)．(2)sinα＝tanαcosα.(3)sin2α＝＝.(4)cos2α＝＝.【常用结论与知识拓展】1．sinα＋cosα，sinαcosα，sinα－cosα三者之的系间关(1)(sinα＋cosα)2＝1＋2sinαcosα.(2)(sinα－cosα)2＝1－2sinαcosα.(3)(sinα＋cosα)2＋(sinα－cosα)2＝2.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(4)(sinα＋cosα)2－(sinα－cosα)2＝4sinαcosα.2．公式可推广要求角诱导归结为k·±α的三角函，只需直接求数值α的三角函，其数值转化程及所得果足：奇偶不，符看象限．其中过结满变变号“奇偶不变变”中的奇、偶分别是指k的奇和偶，不是指函名的化．若是奇倍，正、余弦互；若是偶变与变数称变数则变倍，函名不．数则数称变“符看象限号”是把α成角，原三角函式中的角所在象当锐时数限的三角函的符．数值号题型一：简单的求值问题【要点讲解】(1)利用实现角α的正弦、余弦的互化.(2)利用实现角α的弦切互化.【例1】（2023春•海淀区校级期中）已知，且，则A．B．C．D．【变式训练1】（2022•西湖区校级模拟）已知是第二象限角，且，则A．B．C．D．【变式训练2】（2022•广南县校级学业考试）已知，且为第四象限的角，则的值等于例题精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【变式训练3】（2022春•和平区校级期末）已知，且为第四象限角，则A．B．C．D．题型二：弦化切的求值【要点讲解】(1)形如或的分式,分子、分母同时除以cosα或cos2α,将正、余弦转化为正切,从而求值.(2)形如asin2α+bsinαcosα+ccos2α的式子,将其看成分母为1的分式,再将分母1变形为,转化为形如的式子求值.【例2】（2023春•上饶期末）已知，则A．B．C．D．【变式训练1】（2023春•砚山县校级期中）已知，则的值为A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式训练2】（2023春•顺庆区校级期中）已知，则A．B．C．或1D．或1【变式训练3】（2023•山西模拟）已知，则A．B．C．D．【变式训练4】（2023春•海淀区校级期中）已知，则A．B．C．D．2【变式训练5】（2023春•萍乡期中）已知，则A．0B．C．D．题型三：形如的求值问题【要点讲解】已知sinθ±cosθ求值的问题涉及的三角恒等式(1)(sinθ+cosθ)2=1+2sinθcosθ;(2)(sinθ-cosθ)2=1-2sinθcosθ;(3)(sinθ+cosθ)2+(sinθ-cosθ)2=2;(4)(sinθ-cosθ)2=(sinθ+...