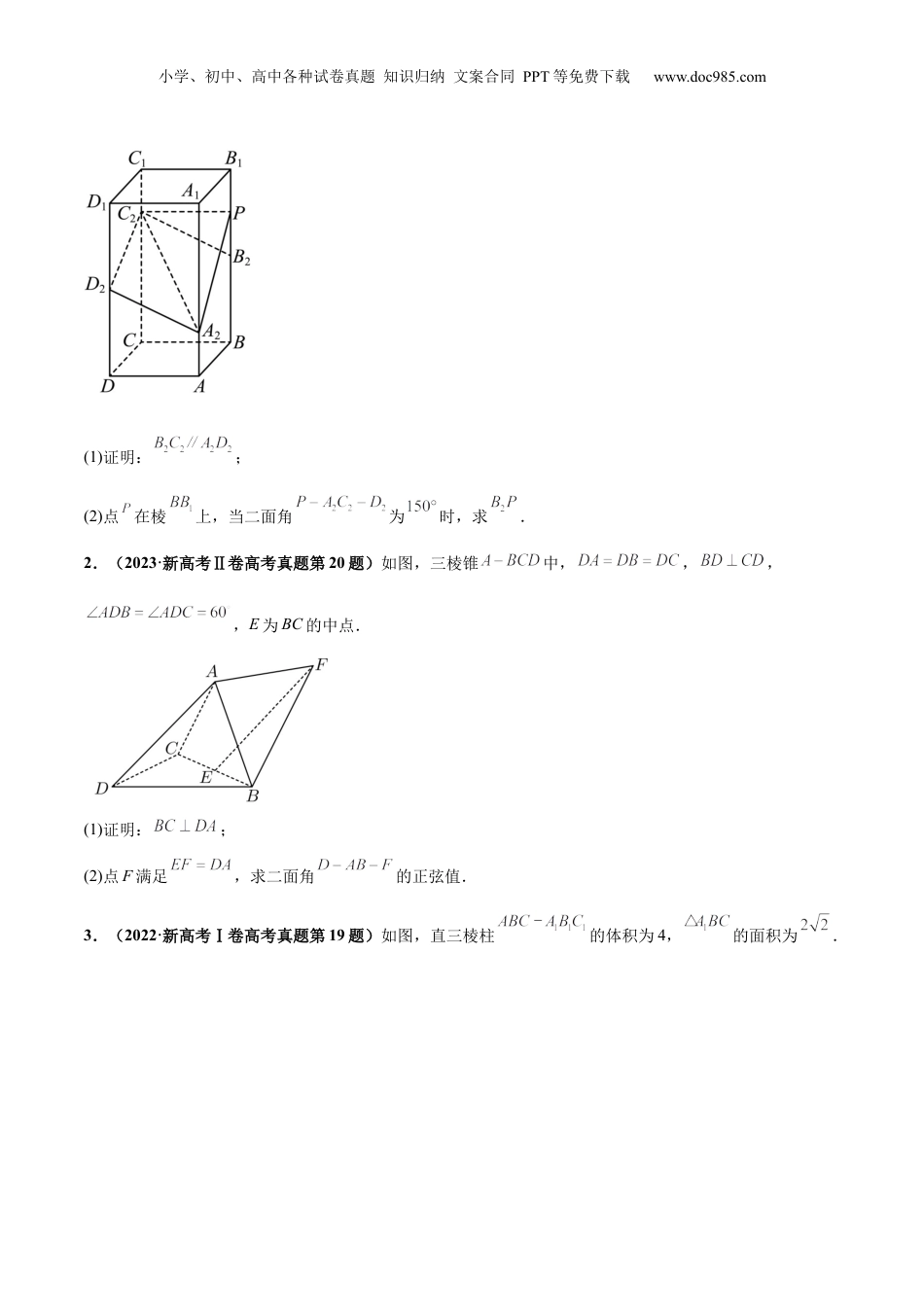
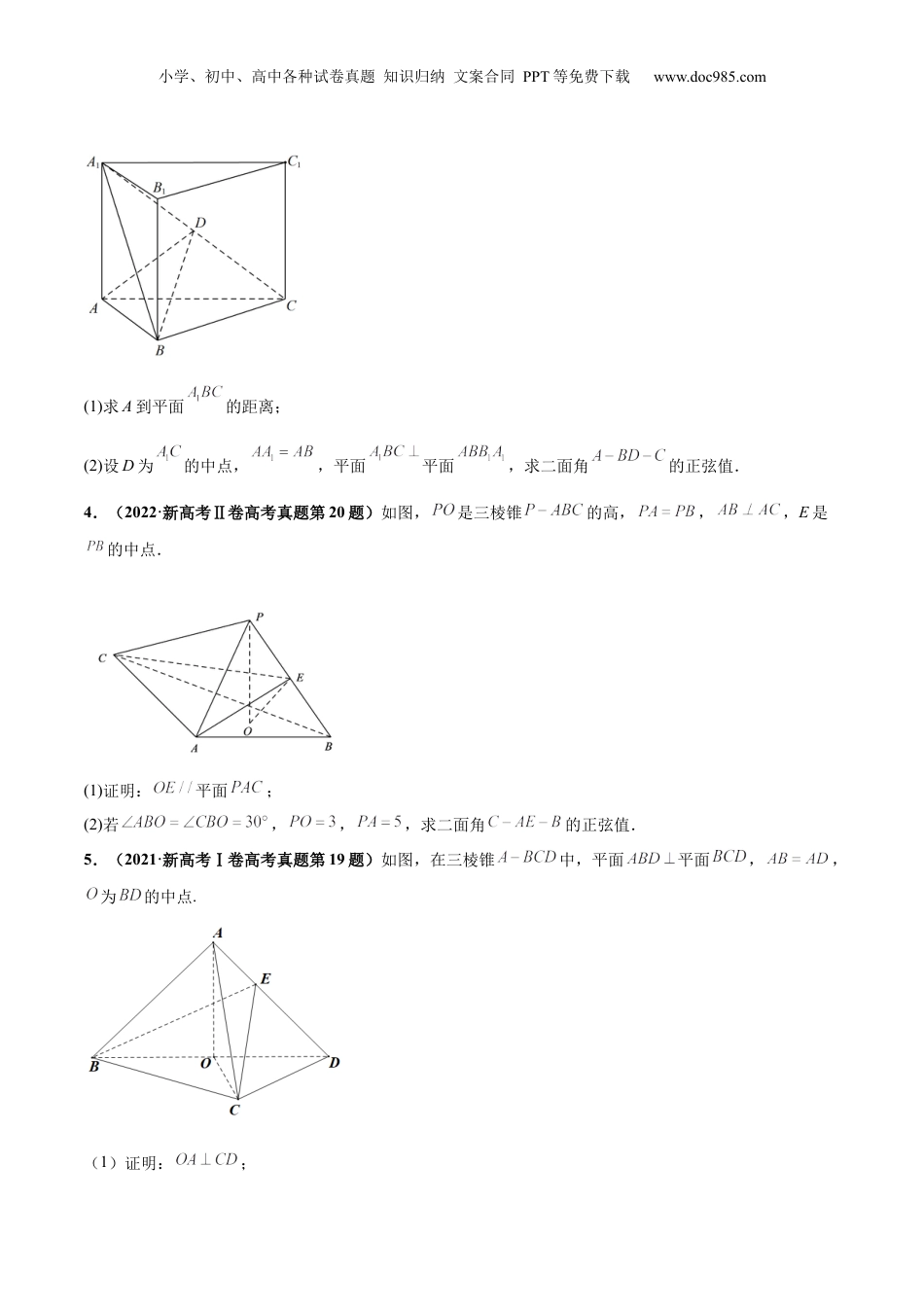
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com押新高考16题立体几何综合（解答题）考点4年考题考情分析立体几何综合2023年新高考Ⅰ卷第18题2023年新高考Ⅱ卷第20题2022年新高考Ⅰ卷第19题2022年新高考Ⅱ卷第20题2021年新高考Ⅰ卷第20题2021年新高考Ⅱ卷第19题2020年新高考Ⅰ卷第20题2020年新高考Ⅱ卷第20题立体几何大题难度一般，纵观近几年的新高考试题，主要考查空间平行关系和空间垂直关系的证明、空间角及空间距离的计算等知识点，同时也是高考冲刺复习的重点复习内容。可以预测2024年新高考命题方向将继续以空间平行关系和空间垂直关系的证明、空间角及空间距离的计算为背景展开命题．1．（2023·新高考Ⅰ卷高考真题第19题）如图，在正四棱柱中，．点分别在棱,上，．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：；(2)点在棱上，当二面角为时，求．2．（2023·新高考Ⅱ卷高考真题第20题）如图，三棱锥中，，，，E为BC的中点．(1)证明：；(2)点F满足，求二面角的正弦值．3．（2022·新高考Ⅰ卷高考真题第19题）如图，直三棱柱的体积为4，的面积为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求A到平面的距离；(2)设D为的中点，，平面平面，求二面角的正弦值．4．（2022·新高考Ⅱ卷高考真题第20题）如图，是三棱锥的高，，，E是的中点．(1)证明：平面；(2)若，，，求二面角的正弦值．5．（2021·新高考Ⅰ卷高考真题第19题）如图，在三棱锥中，平面平面，，为的中点.（1）证明：；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积.6．（2021·新高考Ⅱ卷高考真题第20题）在四棱锥中，底面是正方形，若．（1）证明：平面平面；（2）求二面角的平面角的余弦值．1.空间中的平行关系（1）线线平行（2）线面平行的判定定理：平面外一直线与平面内一直线平行，则线面平行（3）线面平行的性质定理若线面平行，经过直线的平面与该平面相交，则直线与交线平行（4）面面平行的判定定理判定定理1：一个平面内有两条相交直线分别平行于另一个平面，则面面平行判定定理2：一个平面内有两条相交直线分别于另一个平面内两条相交直线平行，则面面平行（5）面面平行的性质定理性质定理1：两平面互相平行，一个平面内任意一条直线平行于另一个平面性质定理2：两平面互相平行，一平面与两平面相交，则交线互相平行2.空间中的垂直关系（1）线线垂直（2）线面垂直的判定定理小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com一直线与平面内两条相交直线垂直，则线面垂直（3）线面垂直的性质定理性质定理1：一直线与平面垂直，则这条直线垂直于平面内的任意一条直线性质定理2：垂直于同一个平面的两条直线平行（4）面面垂直的判定定理一个平面内有一条直线垂直于另一个平面，则两个平面垂直（或：一个平面经过另一个平面的垂线，则面面垂直）（5）面面垂直的性质定理两平面垂直，其中一个平面内有一条直线与交线垂直，则这条直线垂直于另一个平面3.异面直线所成角=（其中（）为异面直线所成角，分别表示异面直线的方向向量）4.直线与平面所成角，(为平面的法向量).5.二面角的平面角（，为平面，的法向量）.6.点到平面的距离（为平面的法向量，是经过面的一条斜线，）.1．（2024·浙江·模拟预测）如图，已知正三棱柱分别为棱的中点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求证：平面；(2)求二面角的正弦值．2．（2024·浙江·二模）如图，在四棱锥中，四边形ABCD是边长为2的正方形，平面平面ABCD，，点E是线段AD的中点，.(1)证明：//平面BDM；(2)求平面AMB与平面BDM的夹角.3．（2024·江苏·一模）如图，在四棱锥中，平面，，，，，点在棱上，且.(1)证明：平面；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(2)当二面角为时，求.4．（2024·浙江·一模）在三棱柱中，四边形是菱形，是等边三...