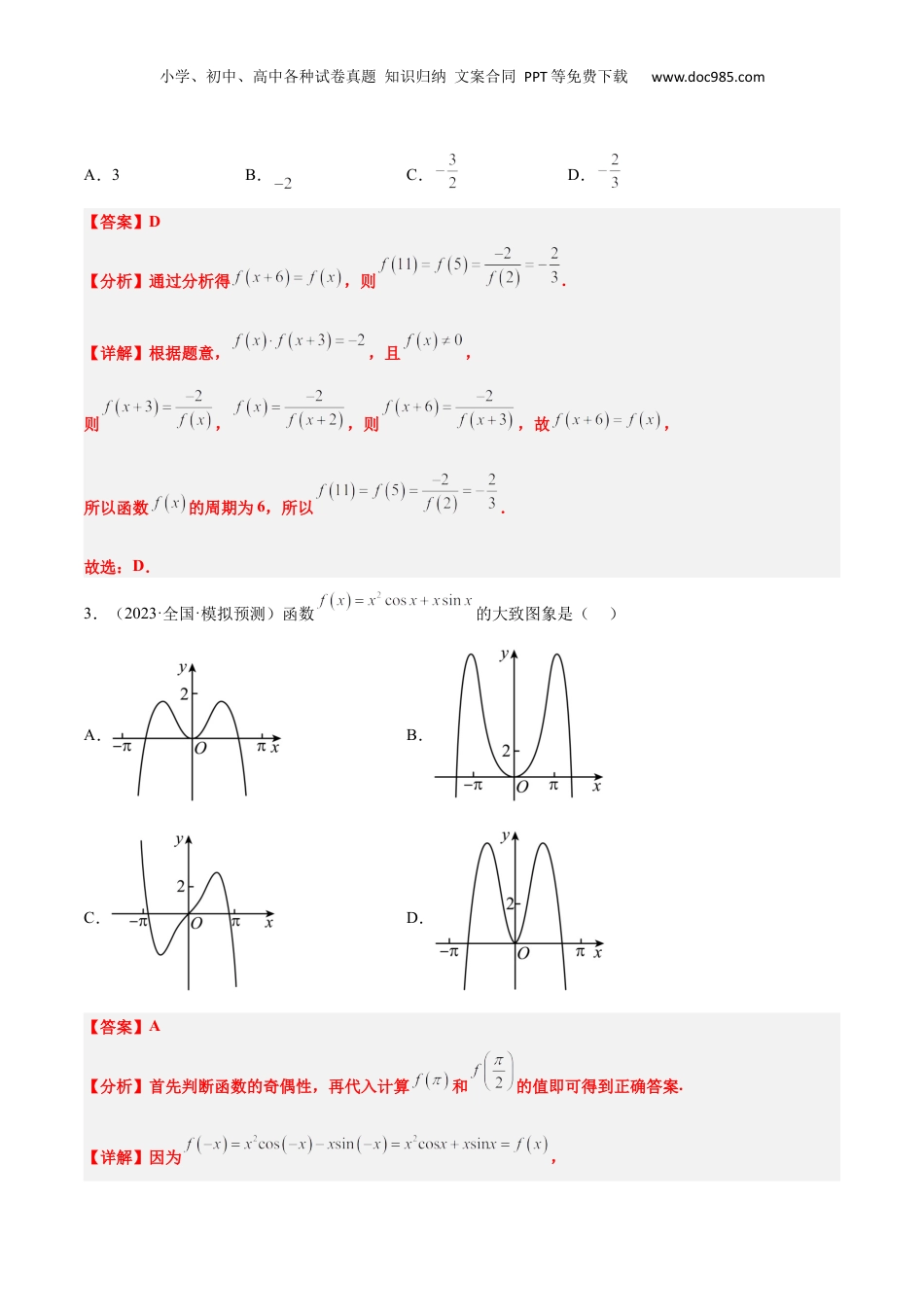
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第08讲函数的基本性质Ⅱ-奇偶性、周期性和对称性（精练）【A组在基础中考查功底】一、单选题1．（2023·北京通州·统考模拟预测）下列函数中，是奇函数且在定义域内单调递增的是（）A．B．C．D．【答案】B【分析】根据幂函数、指数函数、正切函数的单调性及奇偶性逐一判断即可.【详解】对于A，函数在上递减，故A不符题意；对于B，函数的定义域为，关于原点对称，因为，所以函数为奇函数，又函数在单调递增，故B符合题意；对于C，函数的定义域为，关于原点对称，因为，所以函数为偶函数，故C不符合题意；对于D，函数，因为，所以函数不是增函数，故D不符题意.故选：B.2．（2023春·河南·高三校联考阶段练习）已知，函数都满足，又，则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．3B．C．D．【答案】D【分析】通过分析得，则.【详解】根据题意，，且，则，，则，故，所以函数的周期为6，所以．故选：D．3．（2023·全国·模拟预测）函数的大致图象是（）A．B．C．D．【答案】A【分析】首先判断函数的奇偶性，再代入计算和的值即可得到正确答案.【详解】因为，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com且函数定义域为，关于原点对称，所以是偶函数，其图象关于轴对称，排除C；，排除B；，排除D.故选：A.4．（2023·高三课时练习）设是定义在上的偶函数，且在上是严格减函数，，则的解集为（）A．B．C．D．【答案】C【解析】由函数为偶函数可将不等式化为，即可利用单调性求解.【详解】是定义在上的偶函数，，则不等式为，则，在上是严格减函数，，解得或，又定义域为，故不等式的解集为.故选：C.【点睛】本题考查利用偶函数的性质解不等式，将不等式化为利用单调性求解是解题的关键.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（2023·浙江台州·统考二模）已知函数同时满足性质:①;②当时,,则函数可能为()A．B．C．D．【答案】D【分析】①说明为偶函数，②,说明函数在上单调递减,再逐项分析即可.【详解】①说明为偶函数，②,说明函数在上单调递减.A不满足②，B不满足①，C不满足②,因为在单调递减，在单调递增.对于D,满足①,当,单调递减,也满足②.故选：D.6．（2023·黑龙江大庆·铁人中学校考二模）已知函数，若，则实数a的取值范围是（）A．B．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．D．【答案】D【分析】讨论与0、1的大小关系，写出的解析式，解出不等式后，再求并集即为答案.【详解】因为.①当时，.②当时，.③当时，.综上所述：.故选：D.7．（2023春·江西·高三校联考阶段练习）设函数，则（）A．关于对称B．关于对称C．关于对称D．关于对称【答案】D【分析】根据函数对称性的性质依次判断选项即可得到答案.【详解】对选项A，因为，所以不关于对称，故A错误.对选项B，因为，所以不关于对称，故B错误.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com对选项C，因为，，，所以不关于对称，故C错误.对选项D，因为，所以关于对称，故D正确.故选：D8．（2023·青海·校联考模拟预测）已知函数为偶函数，且函数在上单调递增，则关于x的不等式的解集为（）A．B．C．D．【答案】A【分析】利用函数的奇偶性和对称性，得到函数的单调区间，利用单调性解函数不等式.【详解】因为为偶函数，所以的图像关于y轴对称，则的图像关于直线对称．因为在上单调递增，所以在上单调递减．因为，所以，解得．故选：A.二、多选题9．（2023·全国·高三专题练习）已知定义在上的奇函数的图象连续不断，且满足，则以下结论成立的是（）A．函数的周期B．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．点是函数图象的一个对称中心D．在上有4个零点【答案】ABC【分析】根据题意求得函数的周期为，结合函数的周期性和，逐项判定，即可求解.【详解】...