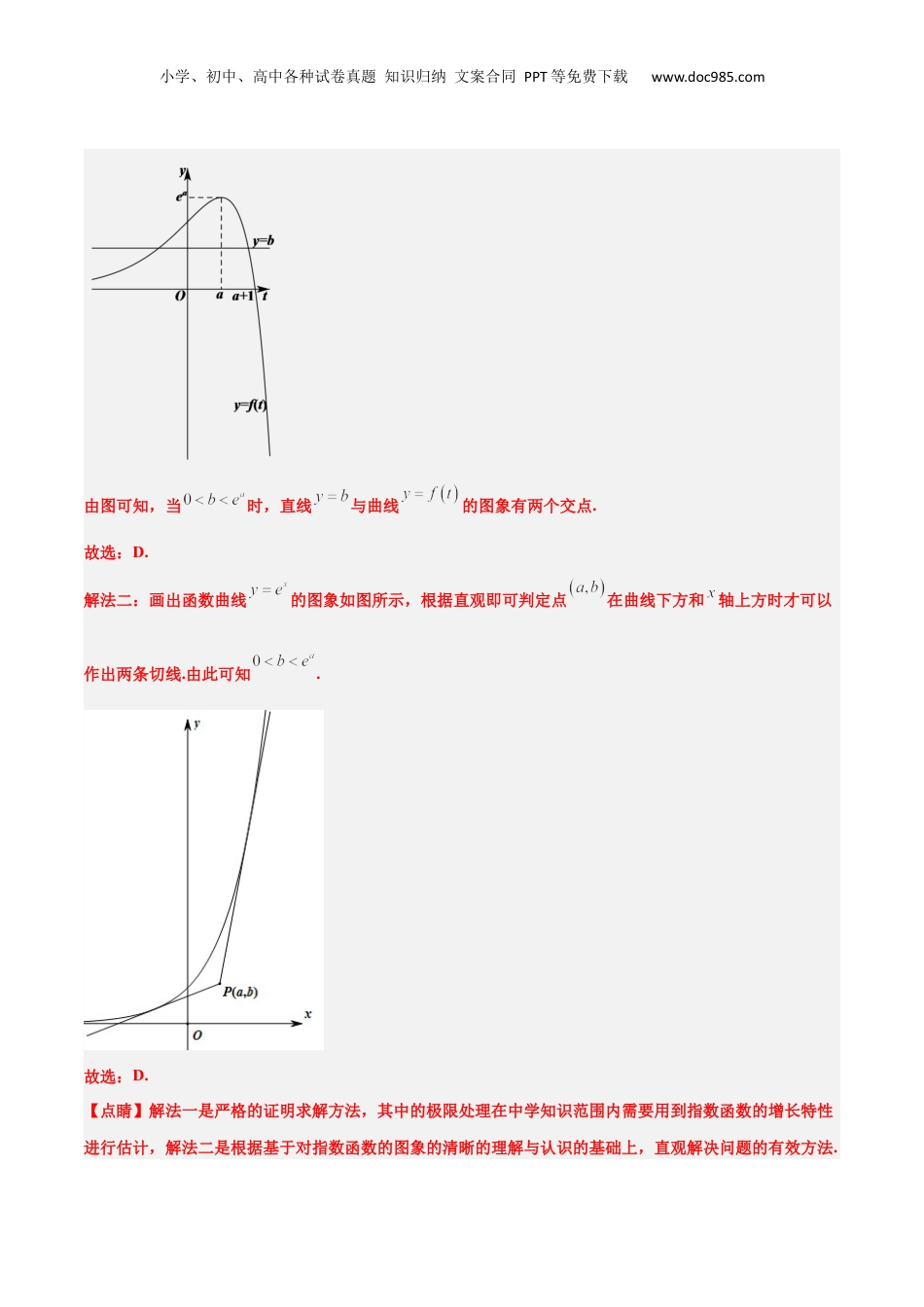
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第14练导数的概念及其意义、导数的运算（精练）一、单选题1．（2021·全国·统考高考真题）若过点可以作曲线的两条切线，则（）A．B．C．D．【答案】D【详解】在曲线上任取一点，对函数求导得，所以，曲线在点处的切线方程为，即，由题意可知，点在直线上，可得，令，则.当时，，此时函数单调递增，当时，，此时函数单调递减，所以，，由题意可知，直线与曲线的图象有两个交点，则，当时，，当时，，作出函数的图象如下图所示：刷真题明导向小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com由图可知，当时，直线与曲线的图象有两个交点.故选：D.解法二：画出函数曲线的图象如图所示，根据直观即可判定点在曲线下方和轴上方时才可以作出两条切线.由此可知.故选：D.【点睛】解法一是严格的证明求解方法，其中的极限处理在中学知识范围内需要用到指数函数的增长特性进行估计，解法二是根据基于对指数函数的图象的清晰的理解与认识的基础上，直观解决问题的有效方法.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二、解答题2．（2021·北京·统考高考真题）已知函数．（1）若，求曲线在点处的切线方程；【答案】（1）；（2）函数的增区间为、，单调递减区间为，最大值为，最小值为.【分析】（1）求出、的值，利用点斜式可得出所求切线的方程；【详解】（1）当时，，则，，，此时，曲线在点处的切线方程为，即；3．（2022·全国·统考高考真题）已知函数(1)当时，求曲线在点处的切线方程；【答案】(1)【分析】（1）先算出切点,再求导算出斜率即可【详解】（1）的定义域为当时,,所以切点为,所以切线斜率为2所以曲线在点处的切线方程为4．（2022·天津·统考高考真题）已知，函数(1)求函数在处的切线方程；【答案】(1)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】（1）求出可求切线方程；【详解】（1），故，而，曲线在点处的切线方程为即.三、填空题5．（2021·全国·统考高考真题）曲线在点处的切线方程为__________．【答案】【分析】先验证点在曲线上，再求导，代入切线方程公式即可．【详解】由题，当时，，故点在曲线上．求导得：，所以．故切线方程为．故答案为：．6．（2022·全国·统考高考真题）若曲线有两条过坐标原点的切线，则a的取值范围是________________．【答案】【分析】设出切点横坐标，利用导数的几何意义求得切线方程，根据切线经过原点得到关于的方程，根据此方程应有两个不同的实数根，求得的取值范围.【详解】 ，∴，设切点为,则,切线斜率,切线方程为：, 切线过原点，∴,小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com整理得：, 切线有两条，∴,解得或,∴的取值范围是,故答案为：7．（2020·全国·统考高考真题）曲线的一条切线的斜率为2，则该切线的方程为______________.【答案】【分析】设切线的切点坐标为，对函数求导，利用，求出，代入曲线方程求出，得到切线的点斜式方程，化简即可.【详解】设切线的切点坐标为，，所以切点坐标为，所求的切线方程为，即.故答案为：.【点睛】本题考查导数的几何意义，属于基础题.四、双空题8．（2022·全国·统考高考真题）曲线过坐标原点的两条切线的方程为____________，____________．【答案】【分析】分和两种情况，当时设切点为，求出函数的导函数，即可求出切线的斜小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com率，从而表示出切线方程，再根据切线过坐标原点求出，即可求出切线方程，当时同理可得；【详解】[方法一]：化为分段函数，分段求分和两种情况，当时设切点为，求出函数导函数，即可求出切线的斜率，从而表示出切线方程，再根据切线过坐标原点求出，即可求出切线方程，当时同理可得；解：因为，当时，设切点为，由，所以，所以切线方程为，又切线过坐标原点，所以，解得，所以切线方程为，即；...