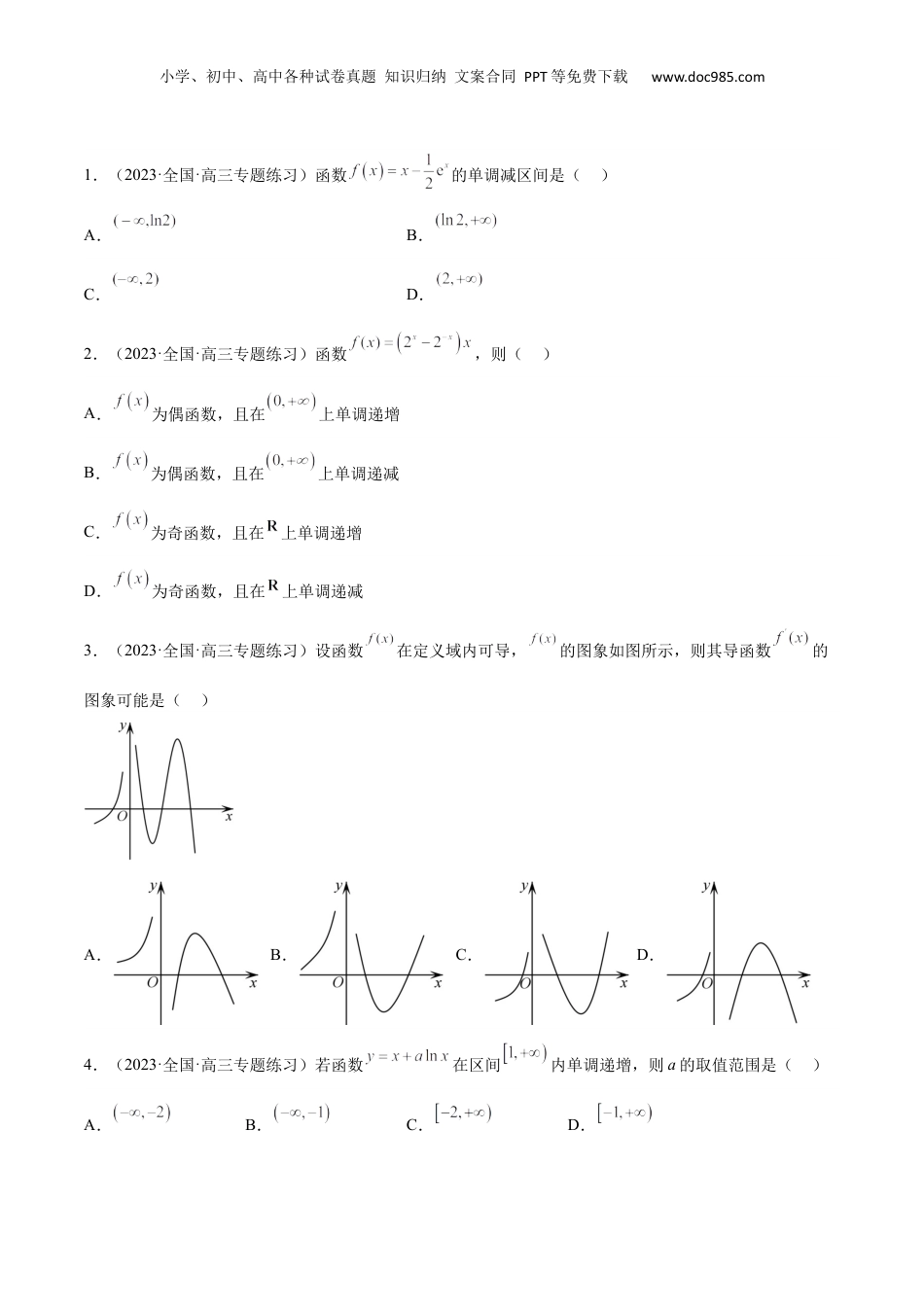
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第15练导数与函数的单调性（精练）一、解答题1．（2022·浙江·统考高考真题）设函数．(1)求的单调区间；2．（2021·全国·统考高考真题）已知函数．（1）讨论的单调性；3．（2021·浙江·统考高考真题）设a，b为实数，且，函数（1）求函数的单调区间；(注：是自然对数的底数)4．（2021·全国·高考真题）设函数，其中.（1）讨论的单调性；5．（2021·全国·统考高考真题）已知且，函数．（1）当时，求的单调区间；【A组在基础中考查功底】一、单选题刷真题明导向小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．（2023·全国·高三专题练习）函数的单调减区间是（）A．B．C．D．2．（2023·全国·高三专题练习）函数，则（）A．为偶函数，且在上单调递增B．为偶函数，且在上单调递减C．为奇函数，且在上单调递增D．为奇函数，且在上单调递减3．（2023·全国·高三专题练习）设函数在定义域内可导，的图象如图所示，则其导函数的图象可能是（）A．B．C．D．4．（2023·全国·高三专题练习）若函数在区间内单调递增，则a的取值范围是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（2023·全国·高三专题练习）若函数在区间上单调递增，则实数k的取值范围是（）A．B．C．D．6．（2023·全国·高三专题练习）若函数存在单调递减区间，则实数b的取值范围是（）A．B．C．D．7．（2023·全国·高三专题练习）已知函数，若对，，都有成立，则的取值范围是（）A．B．C．D．8．（2023·全国·高三专题练习）若为奇函数，则的解集为（）A．B．C．D．9．（2023·全国·高三专题练习）已知，，，则，，的大小关系为（）A．B．C．D．10．（2023·全国·高三专题练习）对任意的，当时，恒成立，则实数的取值范围是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二、多选题11．（2023·北京朝阳·高三专题练习）游人游玩的湖边常设有如图所示的护栏柱与柱之间是一条均匀悬链．数学中把这种两端固定的一条（粗细与质量分布）均匀、柔软的链条，在重力的作用下所具有的曲线形状称为悬链线．如果建立适当的平面直角坐标系，那么悬链线可以表示为函数，其中，则下列关于悬链线函数的性质判断中，正确的有（）.A．为偶函数B．为奇函数C．的最小值为aD．的单调递增区间为12．（2023春·河北邯郸·高三校联考开学考试）已知,若,则（）A．B．C．D．13．（2023春·山西忻州·高三校联考开学考试）已知函数，则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．恒成立B．是上的增函数C．在取得极小值D．只有一个零点三、填空题14．（2023春·宁夏吴忠·高三统考开学考试）设函数，若函数的图象在点处的切线方程为，则函数的单调增区间为__________．15．（2023·全国·高三专题练习）若正实数满足则________16．（2023春·上海普陀·高三曹杨二中校考阶段练习）已知函数，，若在上恒成立，则实数的取值范围是___________.17．（2023·安徽宣城·统考二模）已知函数，则不等式的解集是________．四、解答题18．（2023·全国·高三专题练习）已知函数，讨论的单调性.19．（2023·全国·高三专题练习）已知函数(a∈R且a≠0)，讨论函数的单调性．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【B组在综合中考查能力】一、解答题1．（2023·全国·高三专题练习）已知函数.讨论函数的单调区间；2．（2023·全国·高三专题练习）已知函数，为函数的导函数，讨论的单调性.3．（2023·全国·高三专题练习）已知函数（其中为自然对数的底数），讨论的单调性.4．（2023·全国·高三专题练习）已知函数．当时，讨论函数的单调性；5．（2023·全国·高三专题练习）已知函数，讨论函数的单调性．二、单选题6．（2023·四川宜宾·统考三模）已知函数在区间上单调递增，则实数a的取值...