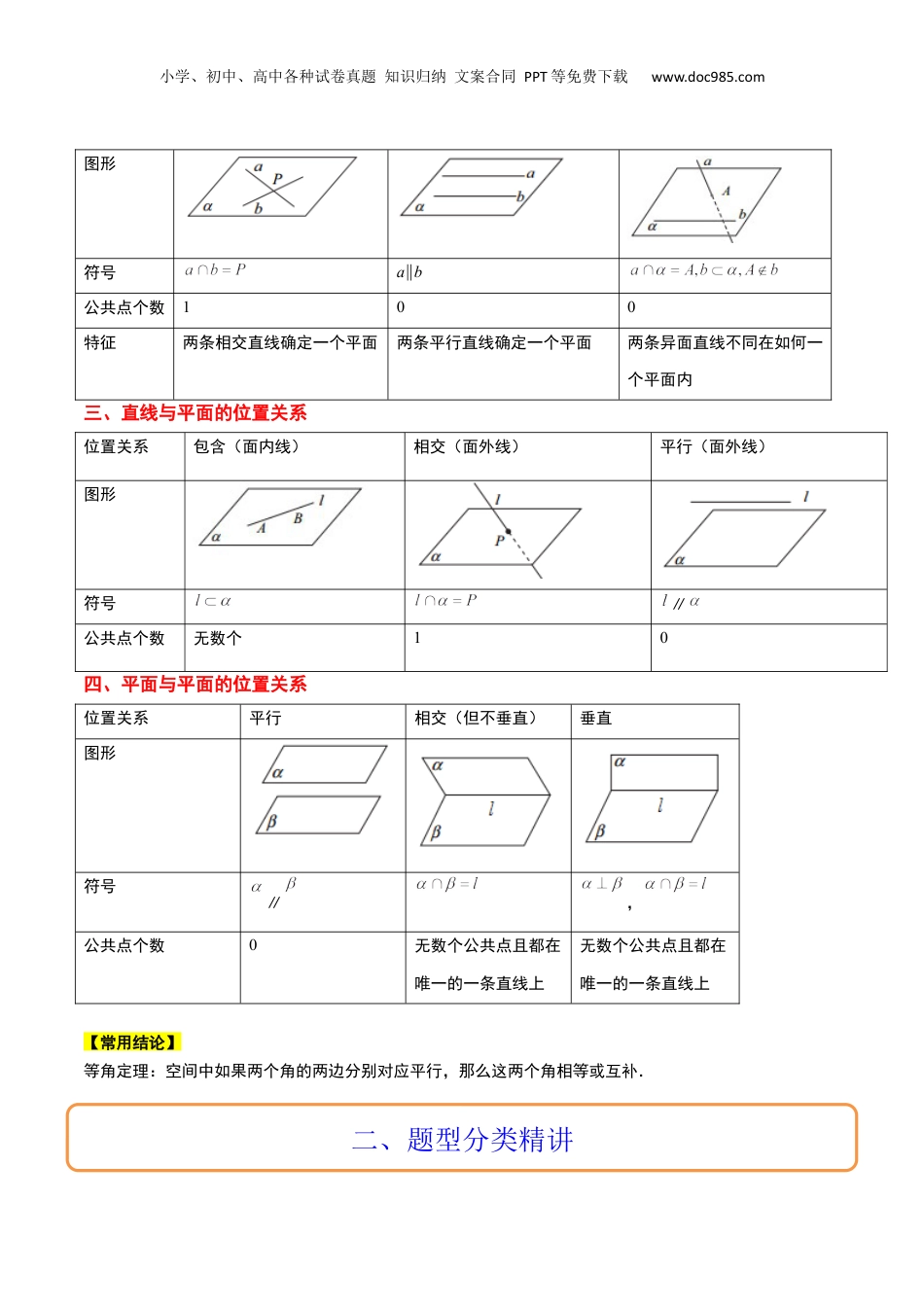
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第32讲空间点、直线、平面间的位置关系（精讲）题型目录一览①共面、共线、共点问题的证明②异面直线③平面的基本性质④等角定理一、四个公理公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内．注意：（1）此公理是判定直线在平面内的依据；（2）此公理是判定点在面内的方法公理2：过不在一条直线上的三点，有且只有一个平面．注意：（1）此公理是确定一个平面的依据；（2）此公理是判定若干点共面的依据推论①：经过一条直线和这条直线外一点，有且只有一个平面；注意：（1）此推论是判定若干条直线共面的依据（2）此推论是判定若干平面重合的依据（3）此推论是判定几何图形是平面图形的依据推论②：经过两条相交直线，有且只有一个平面；推论③：经过两条平行直线，有且只有一个平面；公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．注意：（1）此公理是判定两个平面相交的依据（2）此公理是判定若干点在两个相交平面的交线上的依据（比如证明三点共线、三线共点）（3）此推论是判定几何图形是平面图形的依据公理4：平行于同一条直线的两条直线互相平行．二、直线与直线的位置关系位置关系相交（共面）平行（共面）异面一、知识点梳理小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图形符号a∥b公共点个数100特征两条相交直线确定一个平面两条平行直线确定一个平面两条异面直线不同在如何一个平面内三、直线与平面的位置关系位置关系包含（面内线）相交（面外线）平行（面外线）图形符号∥公共点个数无数个10四、平面与平面的位置关系位置关系平行相交（但不垂直）垂直图形符号∥，公共点个数0无数个公共点且都在唯一的一条直线上无数个公共点且都在唯一的一条直线上【常用结论】等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．二、题型分类精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型一共面、共线、共点问题的证明策略方法共面、共线、共点问题的证明【典例1】如图，在长方体中，、分别是和的中点．(1)证明：、、、四点共面；(2)对角线与平面交于点，交于点，求证：点共线；(3)证明：、、三线共点．【答案】(1)证明见解析；(2)证明见解析；(3)证明见解析.【分析】（1）证明，即可说明、、、四点共面.（2）先证明点面和面，即点在面与面的交线上在证明面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com面，即点，即可得到答案.（3）延长交于,由于面面，则在交线上.【详解】（1）连接在长方体中、分别是和的中点、、、四点共面（2）确定一个平面面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com面对角线与平面交于点面在面与面的交线上面且面面面即点共线.（3）延长交于面面面面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com面面、、三线共点.【题型训练】一、单选题1．（2023·全国·高三专题练习）已知空间四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面内”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【分析】一条直线和直线外一点确定一个平面，由此可验证充分性成立；“这四个点在同一平面内”时，可能有“两点分别在两条相交或平行直线上”，从而必要性不成立．【详解】“这四个点中有三点在同一直线上”，则第四点不在共线三点所在的直线上，因为一条直线和直线外一点确定一个平面，一定能推出“这四点在同一个平面内”，从而充分性成立；“这四个点在同一平面内”时，可能有“两点分别在两条相交或平行直线上”，不一定有三点在同一直线上，从而必要性不成立，所以“这四个点中有三点在同一直线上”是“这四个点在同一平面内”的充分不必要条件.故选：A.2．（2023·全国·高三专题练习）正方体ABCD-A1B1C1D1中，E，...