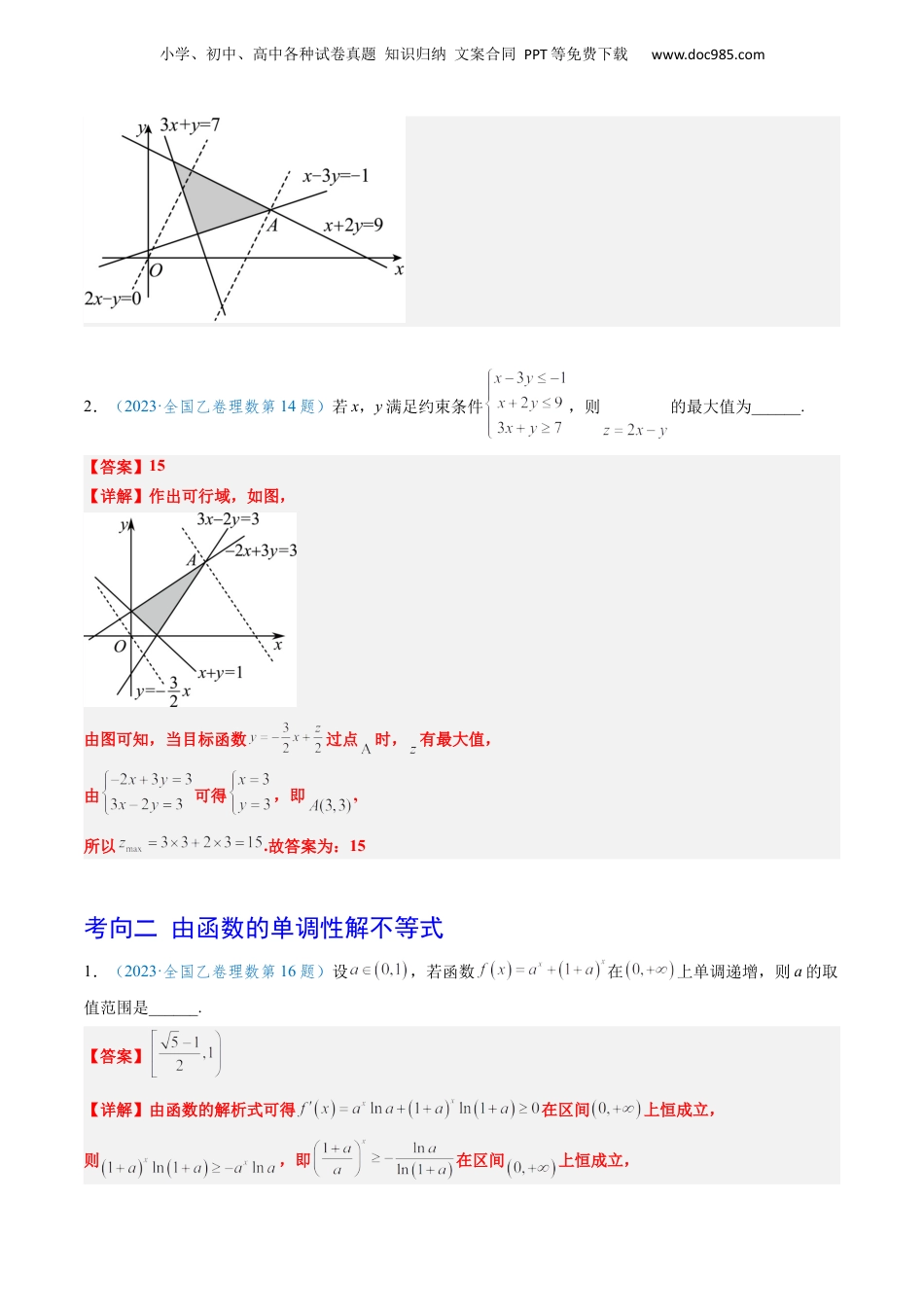
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2023年高考数学真题题源解密（全国卷）专题04不等式与不等关系目录一览①2023真题展现考向一线性规划考向二由函数的单调性解不等式②真题考查解读③近年真题对比考向一线性规划考向二基本不等式及其应用考向三比较大小④命题规律解密⑤名校模拟探源⑥易错易混速记考向一线性规划1．（2023·全国乙卷文数第15题）若x，y满足约束条件，则的最大值为______.【答案】8【详解】作出可行域如下图所示：，移项得，联立有，解得，设，显然平移直线使其经过点，此时截距最小，则最大，代入得，故答案为：8.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2023·全国乙卷理数第14题）若x，y满足约束条件，则的最大值为______.【答案】15【详解】作出可行域，如图，由图可知，当目标函数过点时，有最大值，由可得，即,所以.故答案为：15考向二由函数的单调性解不等式1．（2023·全国乙卷理数第16题）设，若函数在上单调递增，则a的取值范围是______.【答案】【详解】由函数的解析式可得在区间上恒成立，则，即在区间上恒成立，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故，而，故，故即，故，结合题意可得实数的取值范围是.故答案为：.【命题意图】1．二元一次不等式组与简单线性规划问题（1）会从实际情境中抽象出二元一次不等式组.（2）了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组.（3）会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决.2．基本不等式：（1）了解基本不等式的证明过程.（2）会用基本不等式解决简单的最大（小）值问题.【考查要点】线性规划这部分内容主要是以课程学习情境为主，备考以常见的简单题型为主；基本不等式这部分内容在全国卷主要以选做题的形式出现，在2020年的新高考中为多选题，题目难度为中等难度，在备考中以中等难度题型为主训练思维的灵活性，同时注意三个正数的算数—几何平均不等式这一题型；绝对值不等式这部分内容在全国卷中通常为选做题，考查的频率较高，题目的难度为中等难度，在备考中要注意与函数知识相结合【得分要点】高频考点：线性规划中频考点：基本不等式、比较大小低频考点：利用函数单调性解不等式考向一线性规划一、单选题1．（2022·全国乙卷理数第5题）若x，y满足约束条件则的最大值是（）A．B．4C．8D．12小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】C【详解】由题意作出可行域，如图阴影部分所示，转化目标函数为，上下平移直线，可得当直线过点时，直线截距最小，z最大，所以.故选：C.2．（2021·全国乙卷文数第5题）若满足约束条件则的最小值为（）A．18B．10C．6D．4【答案】C【详解】由题意，作出可行域，如图阴影部分所示，由可得点,转换目标函数为，上下平移直线，数形结合可得当直线过点时,取最小值，此时.故选：C.考向二基本不等式及其应用一、单选题1．（2021·全国乙卷文数第8题）下列函数中最小值为4的是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】C【详解】对于A，，当且仅当时取等号，所以其最小值为，A不符合题意；对于B，因为，，当且仅当时取等号，等号取不到，所以其最小值不为，B不符合题意；对于C，因为函数定义域为，而，，当且仅当，即时取等号，所以其最小值为，C符合题意；对于D，，函数定义域为，而且，如当，，D不符合题意．故选：C．二、填空题1．（2022·全国甲卷理数第16题）已知中，点D在边BC上，．当取得最小值时，．【答案】【详解】[方法一]：余弦定理设，则在中，，在中，，所以，当且仅当即时，等号成立，所以当取最小值时，.故答案为：.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com[方法二]：建系法令BD=t，以D为原点，OC为x轴，建立平面直角坐标系.则C（2t,0），A（1，），B（-t,0）[方法三]：余弦定理设BD=x,CD=2x.由余弦定理得，，，，令，则，，，当且仅当，即时等号成立.[方法四...