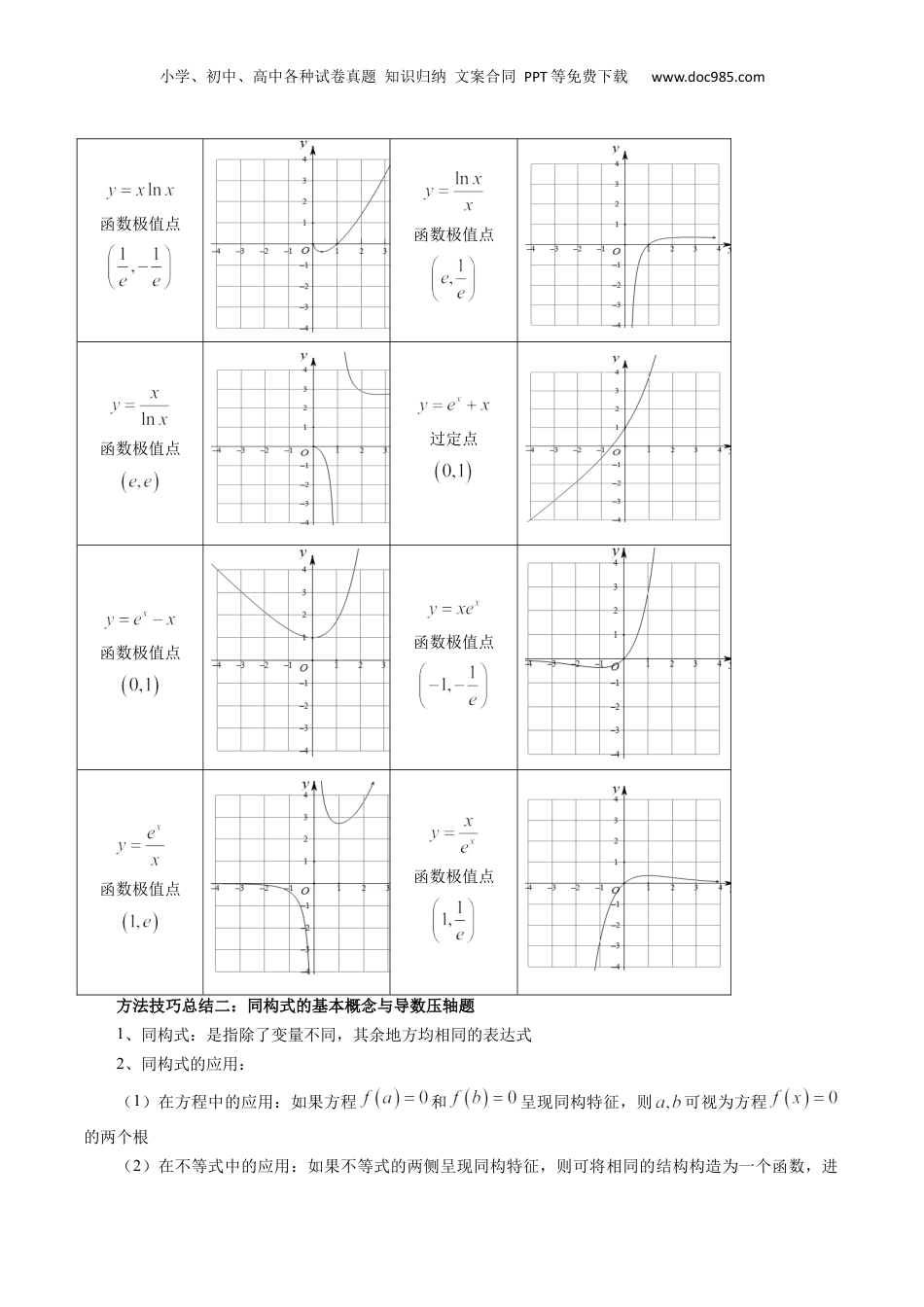
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点突破11导数中的同构问题目录方法技巧总结一、常见的同构函数图像函数表达式图像函数表达式图像函数极值点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com函数极值点函数极值点函数极值点过定点函数极值点函数极值点函数极值点函数极值点方法技巧总结二：同构式的基本概念与导数压轴题1、同构式：是指除了变量不同，其余地方均相同的表达式2、同构式的应用：（1）在方程中的应用：如果方程和呈现同构特征，则可视为方程的两个根（2）在不等式中的应用：如果不等式的两侧呈现同构特征，则可将相同的结构构造为一个函数，进小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com而和函数的单调性找到联系．可比较大小或解不等式．<同构小套路>①指对各一边，参数是关键；②常用“母函数”：，；寻找“亲戚函数”是关键；③信手拈来凑同构，凑常数、、参数；④复合函数（亲戚函数）比大小，利用单调性求参数范围．（3）在解析几何中的应用：如果满足的方程为同构式，则为方程所表示曲线上的两点．特别的，若满足的方程是直线方程，则该方程即为直线的方程（4）在数列中的应用：可将递推公式变形为“依序同构”的特征，即关于与的同构式，从而将同构式设为辅助数列便于求解3、常见的指数放缩：ex≥x+1(x=0);ex≥ex(x=1)4、常见的对数放缩：1−1x≤lnx≤x−1(x=1);lnx≤xe(x=e)5、常见三角函数的放缩：x∈(0,π2),sinx<x<tanx6、学习指对数的运算性质时，曾经提到过两个这样的恒等式：（1）且时，有（2）当且时，有再结合指数运算和对数运算的法则，可以得到下述结论（其中）（3）（4）（5）（6）再结合常用的切线不等式lnxx-1，等，可以得到更多的结论，这里仅以第（3）条为例进行引申：（7）；（8）；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7、同构式问题中通常构造亲戚函数与，常见模型有：①；②；③8、乘法同构、加法同构（1）乘法同构，即乘同构，如；（2）加法同构，即加同构，如，（3）两种构法的区别：①乘法同构，对变形要求低，找亲戚函数与易实现，但构造的函数与均不是单调函数；②加法同构，要求不等式两边互为反函数，构造后的函数为单调函数，可直接由函数不等式求参数范围；题型一：不等式同构例1．（2023·四川达州·高二校考阶段练习）已知，且，，，则（）A．B．C．D．【答案】A【解析】设函数，，当，此时单调递增，当，此时单调递减，由题，，，得，因为，所以，则，且，所以.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故选：A.例2．（2023·湖北黄石·高二校考期中）已知．且，，，则（）A．B．C．D．【答案】B【解析】令，则，即在上单调递减，∴，即，设，则，即在上单调递增，又 ，∴.故选：.例3．（2023·陕西榆林·高二校考期末）已知a，b，，且，，，则a，b，c的大小关系是（）A．B．C．D．【答案】C【解析】构造函数，当时，单调递减，当时，单调递增，，，，因为，所以，即，而a，b，，所以，故选：C变式1．（2023·河南·高二校联考期中）已知，，，则，，的大小顺序是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】D【解析】因为，，，构造函数，其导函数，令，解得：，列表得：+0-极大值所以在上单增.因为，所以，即故选:D.变式2．（2023·全国·高三专题练习）已知，且，其中e为自然对数的底数，则下列选项中一定成立的是（）A．B．C．D．【答案】B【解析】构造，，则恒成立，则，当时，，，当时，，所以在单调递增，在单调递减，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com因为，所以，，又，所以，D错误，因为，所以，，所以，所以，A错误，B正确.令，则，当时，恒成立，所以在上单调递增，当时，，即，因为，所以因为，所以，因为在单调递减，所以，即因为在上单调递减，所以，C错误故选：B变式3．（2023·江西赣州·高二江西省信丰中学校考阶段练习）已知...