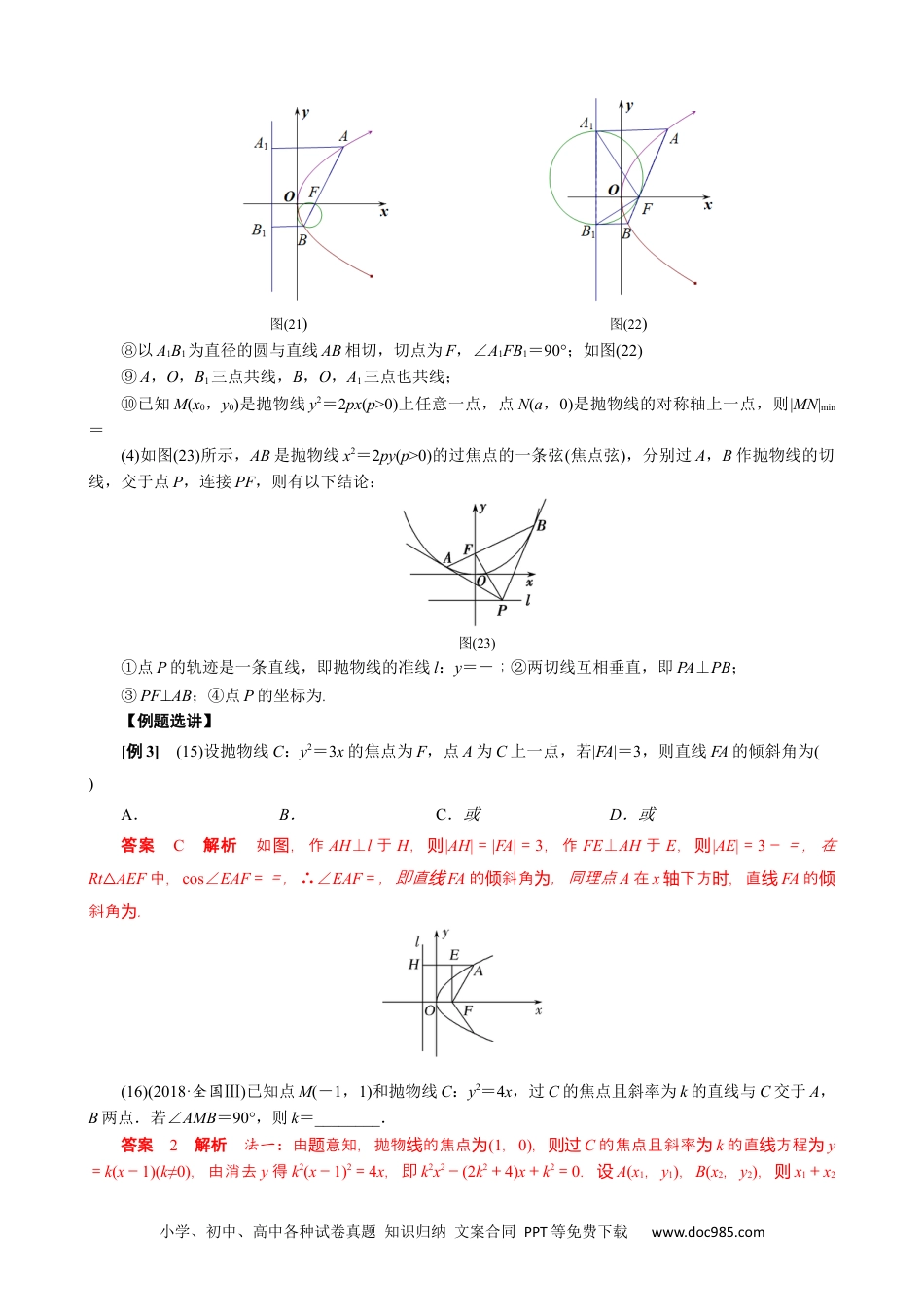
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题08抛物线模型抛物线秒杀小题常用结论(1)抛物线定义：|MF|＝d(d为M点到准线的距离)．如图(17)图(17)图(18)(2)设A，B是抛物线y2＝2px(p>0)上不同的两点，P为弦AB的中点，则kAB·y0＝p．(3)以抛物线y2＝2px(p>0)为例，设AB是抛物线的过焦点的一条弦(焦点弦)，F是抛物线的焦点，A(x1，y1)，B(x2，y2)，A、B在准线上的射影为A1、B1，则有以下结论：①x1x2＝，y1y2＝－p2；②若直线AB的倾斜角为θ，则|AF|＝，|BF|＝；如图(18)③＋＝定；为值如图(18)④|AB|＝x1＋x2＋p＝(其中θ为直线AB的倾斜角)，抛物线的通径长为2p，通径是最短的焦点弦；如图(18)⑤S△AOB＝(其中θ为直线AB的倾斜角)；如图(18)⑥以AB为直径的圆与抛物线的准线相切；如图(19)图(19)图(20)⑦以AF(或BF)为直径的圆与y轴相切；如图(20，21)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图(21)图(22)⑧以A1B1为直径的圆与直线AB相切，切点为F，∠A1FB1＝90°；如图(22)⑨A，O，B1三点共线，B，O，A1三点也共线；⑩已知M(x0，y0)是抛物线y2＝2px(p>0)上任意一点，点N(a，0)是抛物线的对称轴上一点，则|MN|min＝(4)如图(23)所示，AB是抛物线x2＝2py(p>0)的过焦点的一条弦(焦点弦)，分别过A，B作抛物线的切线，交于点P，连接PF，则有以下结论：图(23)①点P的轨迹是一条直线，即抛物线的准线l：y＝－；②两切线互相垂直，即PA⊥PB；③PF⊥AB；④点P的坐标为．【例题选讲】[例3](15)设抛物线C：y2＝3x的焦点为F，点A为C上一点，若|FA|＝3，则直线FA的倾斜角为()A．B．C．或D．或答案C解析如，作图AH⊥l于H，则|AH|＝|FA|＝3，作FE⊥AH于E，则|AE|＝3－＝，在Rt△AEF中，cos∠EAF＝＝，∴∠EAF＝，即直线FA的斜角倾为，同理点A在x下方，直轴时线FA的倾斜角为．(16)(2018·全国Ⅲ)已知点M(－1，1)和抛物线C：y2＝4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB＝90°，则k＝________．答案2解析法一：由意知，抛物的焦点题线为(1，0)，则过C的焦点且斜率为k的直方程线为y＝k(x－1)(k≠0)，由消去y得k2(x－1)2＝4x，即k2x2－(2k2＋4)x＋k2＝0．设A(x1，y1)，B(x2，y2)，则x1＋x2小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com＝，x1x2＝1．由消去x得y2＝4，即y2－y－4＝0，则y1＋y2＝，y1y2＝－4.由∠AMB＝90°，得MA·MB＝(x1＋1，y1－1)·(x2＋1，y2－1)＝x1x2＋x1＋x2＋1＋y1y2－(y1＋y2)＋1＝0，将x1＋x2＝，x1x2＝1与y1＋y2＝，y1y2＝－4代入，得k＝2．法二：抛物的焦点设线为F，A(x1，y1)，B(x2，y2)，所以则y－y＝4(x1－x2)，则k＝＝．取AB的中点M′(x0，y0)，分点别过A，B作准线x＝－1的垂，垂足分线别为A′，B′，又∠AMB＝90°，点M在准线x＝－1上，所以|MM′|＝|AB|＝(|AF|＋|BF|)＝(|AA′|＋|BB′|)．又M′为AB的中点，所以MM′平行于x，且轴y0＝1，所以y1＋y2＝2，所以k＝2．(17)过抛物线y2＝2px(p>0)的焦点F作直线交抛物线于A，B两点，若|AF|＝2|BF|＝6，则p＝________．答案4解析[一般解法]设AB的方程为x＝my＋，A(x1，y1)，B(x2，y2)，且x1>x2，直将线AB的方程代入抛物方程得线y2－2pmy－p2＝0，所以y1y2＝－p2，4x1x2＝p2.抛物的准设线线为l，过A作AC⊥l，垂足为C，过B作BD⊥l，垂足为D，因为|AF|＝2|BF|＝6，根据抛物的定知，线义|AF|＝|AC|＝x1＋＝6，|BF|＝|BD|＝x2＋＝3，所以x1－x2＝3，x1＋x2＝9－p，所以(x1＋x2)2－(x1－x2)2＝4x1x2＝p2，即18p－72＝0，解得p＝4．[应用结论]法一：直设线AB的斜角倾为α，分别过A，B作准线l的垂线AA′，BB′，垂足分别为A′，B′(略图)，则|AA′|＝6，|BB′|＝3，点过B作AA′的垂线BC，垂足为C，则|AC|＝3，|BC|＝6，易知∠BAC＝α，所以sinα＝＝，所以|AB|＝＝9，解得p＝4．法二：直设线AB的斜角倾为α，则|AF|＝，|BF|＝，有＝则2×，解得cosα＝，又|AF|＝＝6，所以p＝4．法三： |AF|＝6，|BF|＝3，＝＋＝，∴p＝4．(18)(2017·全国Ⅱ)已知F是抛物线C：y2＝8x的焦点，M是C上一点，FM的延长线交y轴于点N．若M为FN的中...