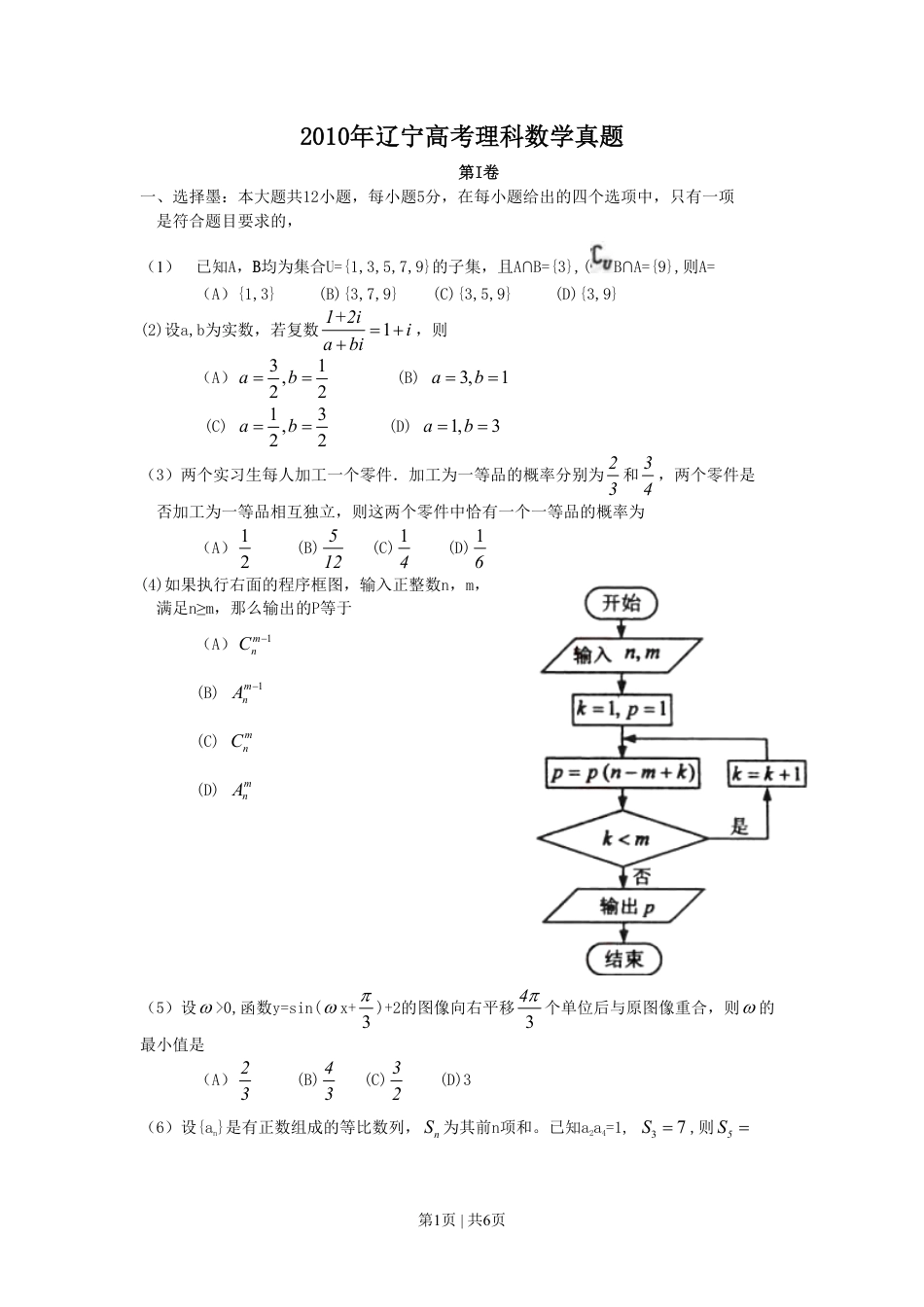
第1页|共6页2010年辽宁高考理科数学真题第I卷一、选择墨：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的，（1）已知A，B均为集合U={1,3,5,7,9}的子集，且A∩B={3},(B∩A={9},则A=（A）{1,3}(B){3,7,9}(C){3,5,9}(D){3,9}(2)设a,b为实数，若复数11+2iiabi=++，则（A）31,22ab==(B)3,1ab==(C)13,22ab==(D)1,3ab==（3）两个实习生每人加工一个零件．加工为一等品的概率分别为23和34，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为（A）12(B)512(C)14(D)16(4)如果执行右面的程序框图，输入正整数n，m，满足n≥m，那么输出的P等于（A）1mnC-(B)1mnA-(C)mnC(D)mnA（5）设w>0,函数y=sin(wx+3p)+2的图像向右平移34p个单位后与原图像重合，则w的最小值是（A）23(B)43(C)32(D)3（6）设{an}是有正数组成的等比数列，nS为其前n项和。已知a2a4=1,37S=,则5S=第2页|共6页（A）152(B)314(C)334(D)172(7)设抛物线y2=8x的焦点为F，准线为l,P为抛物线上一点,PA⊥l,A为垂足．如果直线AF的斜率为-3,那么|PF|=(A)43(B)8(C)83(D)16(8)平面上O,A,B三点不共线，设,OA=aOBb=，则△OAB的面积等于(A)222|||()|abab-g(B)222|||()|abab+g(C)2221|||()2|abab-g(D)2221|||()2|abab+g(9)设双曲线的—个焦点为F；虚轴的—个端点为B，如果直线FB与该双曲线的一条渐近线垂直，那么此双曲线的离心率为(A)2(B)3(C)312+(D)512+(1O)已知点P在曲线y=41xe+上，a为曲线在点P处的切线的倾斜角，则a的取值范围是(A)[0,4p)(B)[,)42pp3(,]24pp(D)3[,)4pp(11)已知a>0，则x0满足关于x的方程ax=6的充要条件是(A)220011,22xRaxbxaxbx$Î-³-(B)220011,22xRaxbxaxbx$Î-£-(C)220011,22xRaxbxaxbx"Î-³-(D)220011,22xRaxbxaxbx"Î-£-(12)(12)有四根长都为2的直铁条，若再选两根长都为a的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则a的取值范围是(A)（0,62+）(B)（1,22）(C)(62-,62+）(D)（0,22）二、填空题：本大题共4小题，每小题5分。（13）261(1)()xxxx++-的展开式中的常数项为_________.（14）已知14xy-<+<且23xy<-<，则23zxy=-的取值范围是_______（答案用区间表示）（15）如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.第3页|共6页（16）已知数列na满足1133,2,nnaaan+=-=则nan的最小值为__________.三、解答题：解答应写出文字说明，证明过程或演算步骤。（17）（本小题满分12分）在△ABC中，a,b,c分别为内角A,B,C的对边，且2sin(2)sin(2)sin.aAacBcbC=+++（Ⅰ）求A的大小；（Ⅱ）求sinsinBC+的最大值.（18）（本小题满分12分）为了比较注射A,B两种药物后产生的皮肤疱疹的面积，选200只家兔做试验，将这200只家兔随机地分成两组，每组100只，其中一组注射药物A，另一组注射药物B。（Ⅰ）甲、乙是200只家兔中的2只，求甲、乙分在不同组的概率；（Ⅱ）下表1和表2分别是注射药物A和B后的试验结果.（疱疹面积单位：mm2）表1：注射药物A后皮肤疱疹面积的频数分布表（ⅰ）完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；第4页|共6页（ⅱ）完成下面2×2列联表，并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.表3：（19）（本小题满分12分）已知三棱锥P－ABC中，PA⊥ABC，AB⊥AC，PA=AC=½AB，N为AB上一点，AB=4AN,M,S分别为PB,BC的中点.（Ⅰ）证明：CM⊥SN；（Ⅱ）求SN与平面CMN所成角的大小.(20)（本小题满分12分）设椭圆C：22221(0)xyabab+=>>的左焦点为F，过点F的直线与椭圆C相交于A，B两点，直线l的倾斜角为60o,2AFFB=uuuruuur.第5页|共6页(I)求椭圆C的离心率；(II)如果|AB|=154，求椭圆C的方程.（21）（本小题满分12分）已知函数1ln)1()(2+++=axxaxf（I）讨论函数)(xf的单调性；（II）设1-<a.如果对任意),0(,21+Îxx，||4)()(|2121xxxfxf-³-，求a的取值范围。请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所作的第一题记分。作答时用2B铅笔在答题卡上吧所选题目对应题号下方的方框...