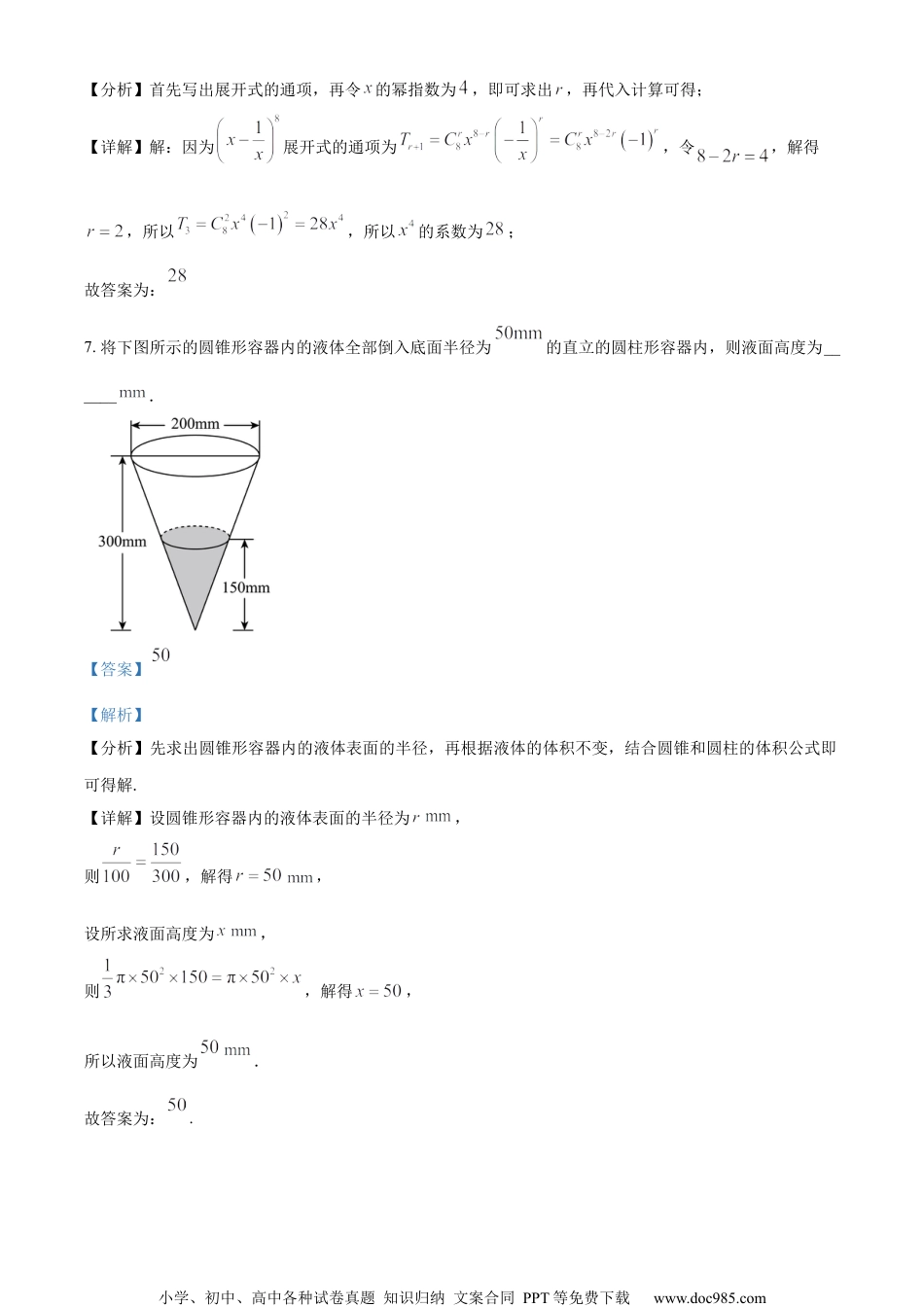
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2023届松江区高三二模考试数学试卷2023.04一、填空题1.已知集合，，则______．【答案】【解析】【分析】根据先解不等式求集合，再应用交集的概念进行运算即可.【详解】因为，,所以.故答案为:.2.若复数z满足，则___________【答案】5【解析】【分析】利用复数的运算法则，算出和，再求模即可【详解】故答案为：53.已知空间向量，，，若，则______．【答案】【解析】【详解】，，，，解得，故答案为：.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4.已知随机变量X服从正态分布，若，则______．【答案】0.94【解析】【分析】根据正态分布的对称性即可求出指定区间的概率.【详解】由正态分布的对称性得.故答案为：0.94.5.已知，且，则______．【答案】【解析】【分析】利用同角三角函数的基本关系结合二倍角公式即可.【详解】，，，.,.故答案为：.6.在的展开式中，的系数为_______．（用数字作答）【答案】【解析】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】首先写出展开式的通项，再令的幂指数为，即可求出，再代入计算可得；【详解】解：因为展开式的通项为，令，解得，所以，所以的系数为；故答案为：7.将下图所示的圆锥形容器内的液体全部倒入底面半径为的直立的圆柱形容器内，则液面高度为______．【答案】【解析】【分析】先求出圆锥形容器内的液体表面的半径，再根据液体的体积不变，结合圆锥和圆柱的体积公式即可得解.【详解】设圆锥形容器内的液体表面的半径为，则，解得，设所求液面高度为，则，解得，所以液面高度为．故答案为：.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8.现从名男医生和名女医生中抽取两人加入“援沪医疗队”，用表示事件“抽到的两名医生性别同”，表示事件“抽到的两名医生都是女医生”，则__________.【答案】【解析】【分析】结合分类计数原理，计算出抽到的两名医生性别相同的概率，计算出抽到的两名医生都是女医生的概率，从而结合条件概率的计算公式即可求出.【详解】由题意知，，，所以.故答案为：.9.参考《九章算术》中“竹九节”问题，提出：一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共2升，下面3节的容积共3升，则第5节的容积为______升．【答案】【解析】【分析】设自上而下的竹子容量依次为，可得为等差数列，根据，，可得数列的通项公式及【详解】设自上而下的竹子容量依次为，可得为等差数列，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则，解得，故，，故答案为：.10.若，则的最小值为_____________________【答案】9【解析】【分析】化简=，利用基本不等式可求得其最小值.【详解】=，当时等号成立，所以的最小值为，故答案为.【点睛】本题主要考查同角三角函数之间的关系，利用基本不等式求最值，属于难题.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用或时等号能否同时成立）.11.已知函数为上的奇函数；且，当时，，则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com______．【答案】##【解析】【分析】首先证明得，则根据其周期性得，再求出，最后相加即可.【详解】因为，为上的奇函数，所以，所以为周期为2的周期函数，因为当时,,则，令,得,,又因为为奇函数，则，所以，则，则，所以，所以，故答案为：.12.已知点是平面直角坐标系中关于轴对称的两点，且．若存在，使得与垂直，且，则的最小值为______．【答案】【解析】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】设，，根据向量线性运算可得，设，则，由向量垂直的坐标表示可构造方程，结合二次函数最值求法可求得，由可求得最小值.【详解】设在...