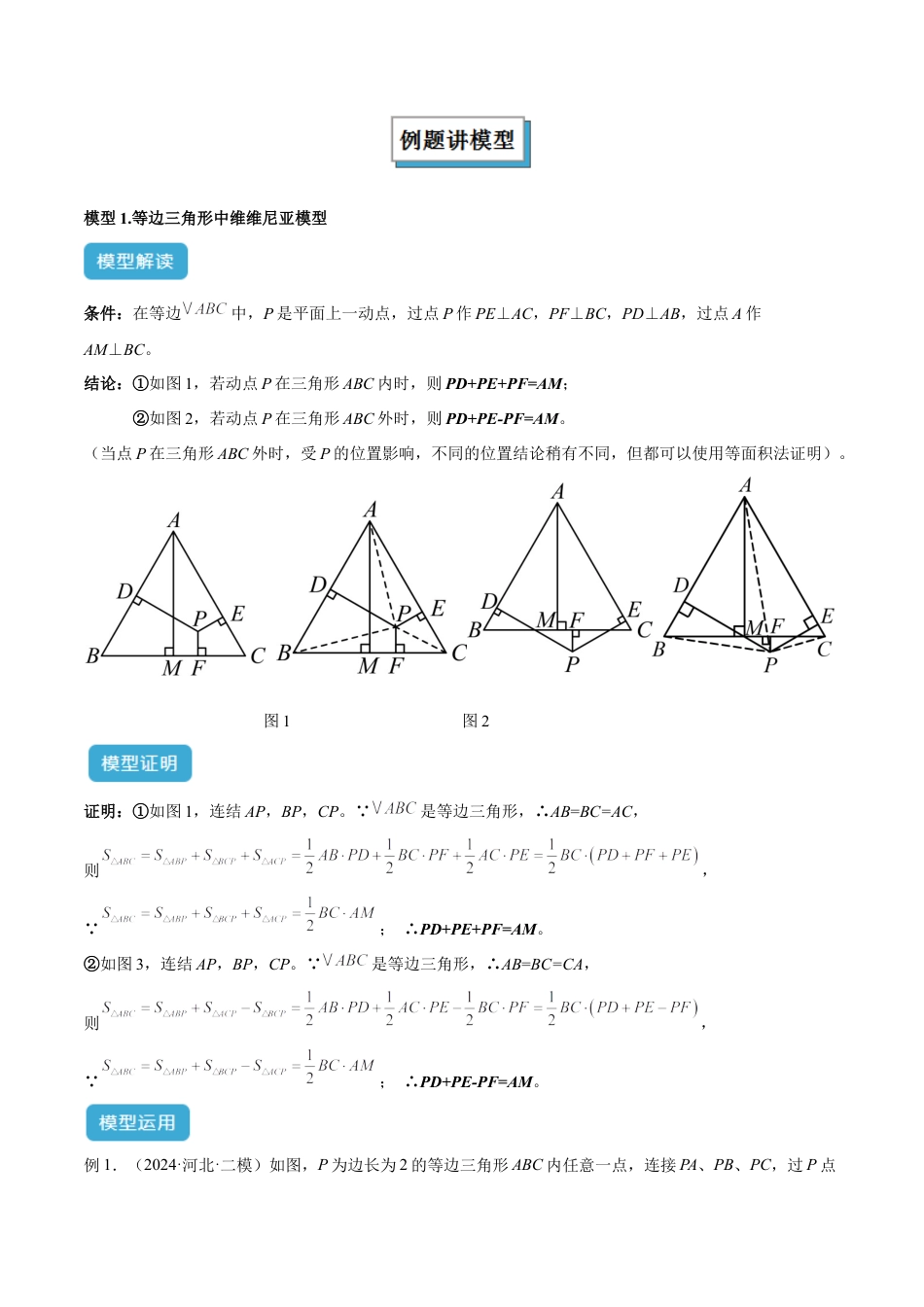
专题13等腰（等边）三角形中的重要模型之维维尼亚模型维维亚尼定理（Viviani'stheorem）：在等边三角形内任意一点P到三边的垂直距离之和，等于该等边三角形的高。这个定理可一般化为：等角多边形内任意一点P跟各边的垂直距离之和，是不变的，跟该点的位置无关。它以温琴佐·维维亚尼命名。而今天我们要学习的维维亚尼模型就是维维亚尼定理及其拓展，它的证明主要利用了等面积法，消去相等底边后得到高之间的关系，因此等腰三角形的维维亚尼模型动点只能在底边所在直线上运动，此时连接点和底边所对顶点，能江原图分割成两个底相等的三角形。.................................................................................................................................................2模型1.等边三角形中维维尼亚模型...............................................................................................................2模型2.等腰三角形中维维尼亚模型...............................................................................................................7...............................................................................................................................................14模型1.等边三角形中维维尼亚模型条件：在等边中，P是平面上一动点，过点P作PE⊥AC，PF⊥BC，PD⊥AB，过点A作AM⊥BC。结论：①如图1，若动点P在三角形ABC内时，则PD+PE+PF=AM；②如图2，若动点P在三角形ABC外时，则PD+PE-PF=AM。（当点P在三角形ABC外时，受P的位置影响，不同的位置结论稍有不同，但都可以使用等面积法证明）。图1图2证明：①如图1，连结AP，BP，CP。 是等边三角形，∴AB=BC=AC，则， ；∴PD+PE+PF=AM。②如图3，连结AP，BP，CP。 是等边三角形，∴AB=BC=CA，则， ；∴PD+PE-PF=AM。例1．（2024·河北·二模）如图，P为边长为2的等边三角形ABC内任意一点，连接PA、PB、PC，过P点分别作BC、AC、AB边的垂线，垂足分别为D、E、F，则PD+PE+PF等于（）A．B．C．2D．【答案】B【分析】求出等边三角形的高，再根据△ABC的面积等于△PAB、△PBC、△PAC三个三角形面积的和，列式并整理即可得到PD＋PE＋PF等于三角形的高．【详解】解： 正三角形的边长为2，∴高为2×sin60°＝，∴S△ABC＝×2×＝， PD、PE、PF分别为BC、AC、AB边上的高，∴S△PBC＝BC•PD，S△PAC＝AC•PE，S△PAB＝AB•PF， AB＝BC＝AC，∴S△PBC+S△PAC+S△PAB＝BC•PD+AC•PE+AB•PF＝×2（PD+PE+PF）＝PD+PE+PF， S△ABC＝S△PBC+S△PAC+S△PAB，∴PD+PE+PF＝．故选B．【点睛】本题利用等边三角形三边相等的性质和三角形的面积等于被分成的三个三角形的面积的和求解．例2．（2024八年级·广东·培优）如图，点P为等边外一点，设点P到三边的距离，且，则的面积等于（）A．B．C．D．【答案】C【分析】本题考查等边三角形的性质，连接、、，过B作于点G，根据面积相等得出，求出，得出，即可求出面积．【详解】解：如图，连接、、，过B作于点G， ，，，，∴，∴．故选：C例3．（23-24八年级上·浙江宁波·期中）如图，P是等边三角形内一点，且，，，以下3个结论：①；②；③；④若点P到三边的距离分别为，，，则有，其中正确的有（）A．4个B．3个C．2个D．1个【答案】B【分析】将绕点A顺时针旋转，得到，连接，由全等三角形的性质可得，，，可证是等边三角形，由勾股定理的逆定理可求，取中点Q，连接，根据直角三角形斜边中线性质可求，进判断为等边三角形，，可得，，可判断①，由勾股定理可求的长，可判断②，由三角形的面积公式可求的面积，可判断③，由三角形的面积公式可求的值，即可判断④．【详解】解：如图，将绕点A顺时针旋转，得到，连接，∴，，∴，，，∴是等边三角形，∴，， ，，∴，∴，取中点Q，连接，∴，∴是等边三角形，∴， ，∴，又∴，∴，∴，∴，故①错误； ，∴，故②正确；∴，故③正确，如图，∴，∴，故④正确，故选：B．【点睛】本题是三角形综合题，考查了等边三角形的性质，勾股定理的逆定理，旋转的性质...