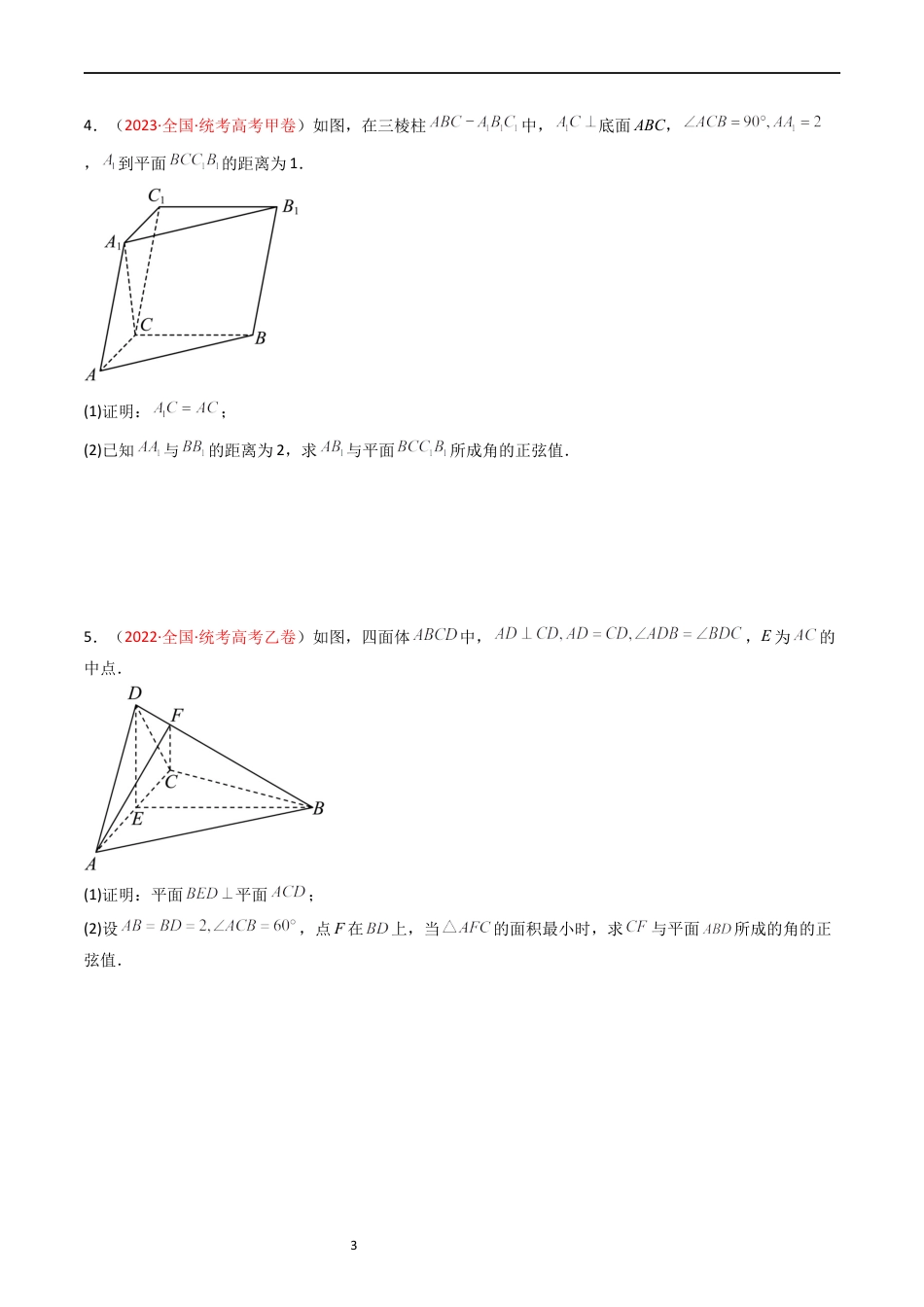
1五年（2019-2023）年高考真题分项汇编专题05立体几何（解答题）立体几何在理科数解答题中一般出现在20题左右的位置。主要考查空间几何体对应的空间角问题，考查二面角的频率比较大。1．（2023·全国·新课标Ⅰ卷）如图，在正四棱柱中，．点分别在棱,上，．(1)证明：；(2)点在棱上，当二面角为时，求．2．（20203全国·统考新课标Ⅱ卷）如图，三棱锥中，，，2，E为BC的中点．(1)证明：；(2)点F满足，求二面角的正弦值．3．（2023·全国·统考高考乙卷）如图，在三棱锥中，，，，，BP，AP，BC的中点分别为D，E，O，，点F在AC上，.(1)证明：平面；(2)证明：平面平面BEF；(3)求二面角的正弦值.34．（2023·全国·统考高考甲卷）如图，在三棱柱中，底面ABC，，到平面的距离为1．(1)证明：；(2)已知与的距离为2，求与平面所成角的正弦值．5．（2022·全国·统考高考乙卷）如图，四面体中，，E为的中点．(1)证明：平面平面；(2)设，点F在上，当的面积最小时，求与平面所成的角的正弦值．46．（2022·全国·统考高考甲卷）在四棱锥中，底面．(1)证明：；(2)求PD与平面所成的角的正弦值．7．（2022·全国·新课标Ⅰ卷）如图，直三棱柱的体积为4，的面积为．(1)求A到平面的距离；(2)设D为的中点，，平面平面，求二面角的正弦值．58．（2022全国·统考新课标Ⅱ卷）如图，是三棱锥的高，，，E是的中点．(1)证明：平面；(2)若，，，求二面角的正弦值．9．（2021·全国·统考高考乙卷）如图，四棱锥的底面是矩形，底面，，为的中点，且．（1）求；（2）求二面角的正弦值．610．（2021·全国·统考高考甲卷）已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，D为棱上的点．（1）证明：；（2）当为何值时，面与面所成的二面角的正弦值最小?11．（2021·全国·新课标Ⅰ卷）如图，在三棱锥中，平面平面，，为的中点.（1）证明：；（2）若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积.712．（2021全国·统考新课标Ⅱ卷）在四棱锥中，底面是正方形，若．（1）证明：平面平面；（2）求二面角的平面角的余弦值．13．（2020·全国·Ⅰ卷）如图，为圆锥的顶点，是圆锥底面的圆心，为底面直径，．是底面的内接正三角形，为上一点，．（1）证明：平面；（2）求二面角的余弦值．814．（2020·全国·新课标Ⅰ卷）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．15．（2020全国·统考新课标Ⅱ卷）如图，四棱锥P-ABCD的底面为正方形，PD底面ABCD．设平面PAD与平面PBC的交线为．（1）证明：平面PDC；（2）已知PD=AD=1，Q为上的点，QB=，求PB与平面QCD所成角的正弦值．916．（2020全国·统考新课标Ⅱ卷）如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN所成角的正弦值.17．（2019·全国·统考Ⅰ卷）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值．1018．（2019全国·统考Ⅱ卷）如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.