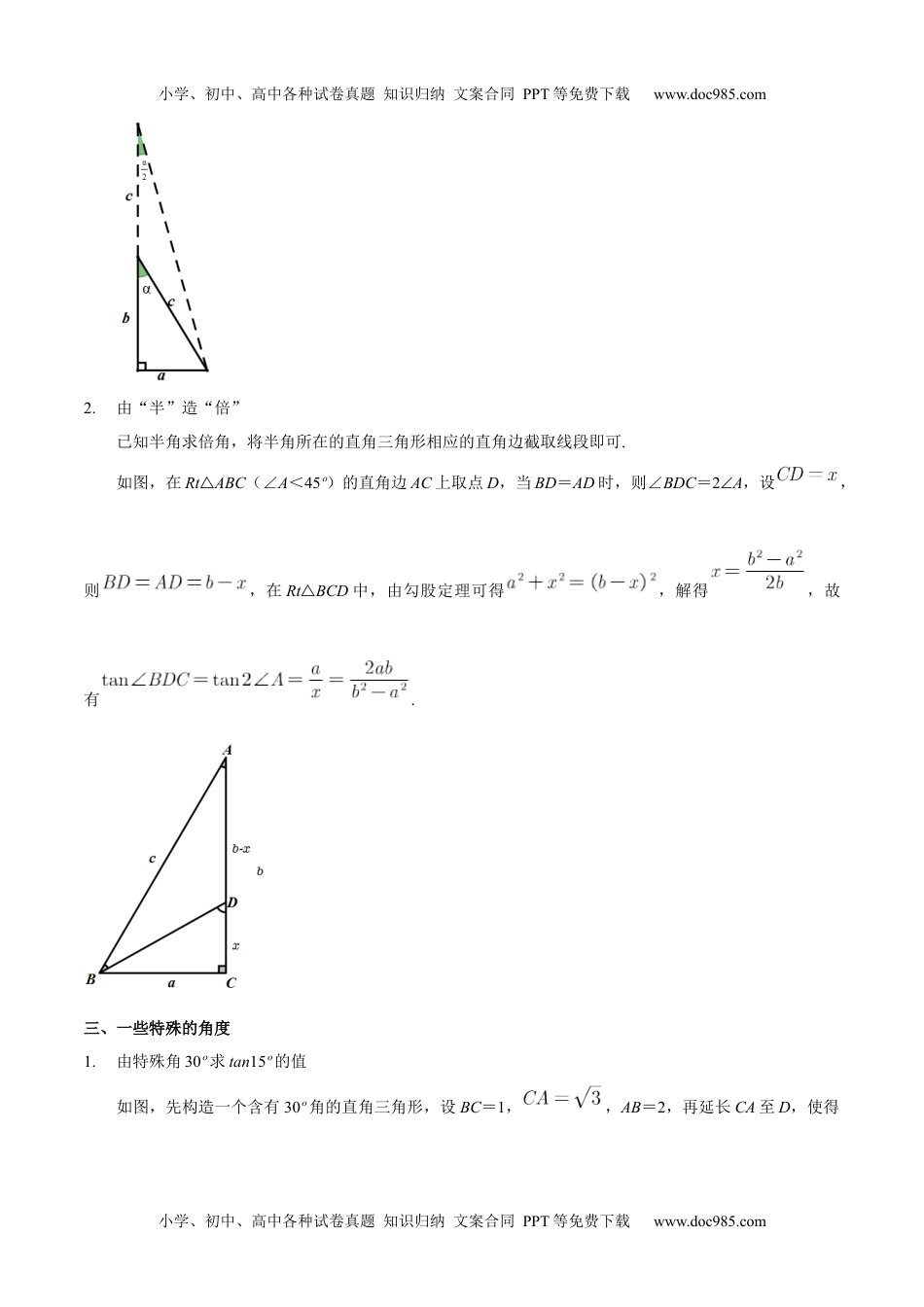
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com倍半角模型知识精讲一、二倍角模型处理方法1.作二倍角的平分线，构成等腰三角形.例：如图，在△ABC中，∠ABC＝2∠C，作∠ABC的平分线交AC于点D，则∠DBC＝∠C，DB＝DC，即△DBC是等腰三角形.2.延长二倍角的一边，使其等于二倍角的另一边，构成两个等腰三角形.例：如图，在△ABC中，∠B＝2∠C，延长CB到点D，使得BD＝AB，连接AD，则△ABD、△ADC都是等腰三角形.例题：如图，在△ABC中，∠C＝2∠A，AC＝2BC，求证：∠B＝90º.【解答】见解析【证法一】如图1，作∠C的平分线CE交AB于点E，过点E作ED⊥AC于点D.则∠ACE＝∠A，AE＝CE，∵AE＝EC，ED⊥AC，∴CD＝AC，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com又∵AC＝2BC，∴CD＝CB，∴△CDE△≌CBE，∴∠B＝∠CDE＝90º；【证法二】如图2，延长AC到点D，使得CD＝CB，连接BD，取AC的中点E，连接BE.由题意可得EC＝CD＝BC，∠DBE＝90º，∵CD＝CB，∠D＝∠CBD，∴∠ACB＝2∠D，∵∠ACB＝2∠A，∠A＝∠D，∴AB＝BD，又∵AE＝DC，∴△ABE≌△DBC，∴∠ABE＝∠DBC，∴∠ABC＝∠EBD＝90º.【证法三】如图3，作∠C的平分线CD，延长CB到点E，使得CE＝AC，∴AC＝BC＋BE.∵AC＝2BC，∴BC＝BE，在△ACD与△ECD中，AC＝EC，∠ACD＝∠ECD，CD＝CD，∴△ACD≌△ECD，∴∠A＝∠E，又∵∠DCB＝∠DCA＝∠A，∴∠E＝∠DCB，∴DC＝DE，∴∠ABC＝90º.二、倍半角综合1.由“倍”造“半”已知倍角求半角，将倍角所在的直角三角形相应的直角边顺势延长即可.如图，若，则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2.由“半”造“倍”已知半角求倍角，将半角所在的直角三角形相应的直角边截取线段即可.如图，在Rt△ABC（∠A＜45º）的直角边AC上取点D，当BD＝AD时，则∠BDC＝2∠A，设，则，在Rt△BCD中，由勾股定理可得，解得，故有.三、一些特殊的角度1.由特殊角30º求tan15º的值如图，先构造一个含有30º角的直角三角形，设BC＝1，，AB＝2，再延长CA至D，使得小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comAD＝AB＝2，连接BD，构造等腰△ABD，则∠D＝∠BAC＝15º，.2.由特殊角45º求tan22.5º的值由图可得，.3.“345”三角形（1）如图1，Rt△ABC三边比为3:4:5，Rt△BCD三边比为，若，则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com；（2）如图2，Rt△ABC三边比为3:4:5，Rt△BCD三边比为，若，则；（3）如图3，Rt△ABC三边比为3:4:5，Rt△BCD三边比为，若，则.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com