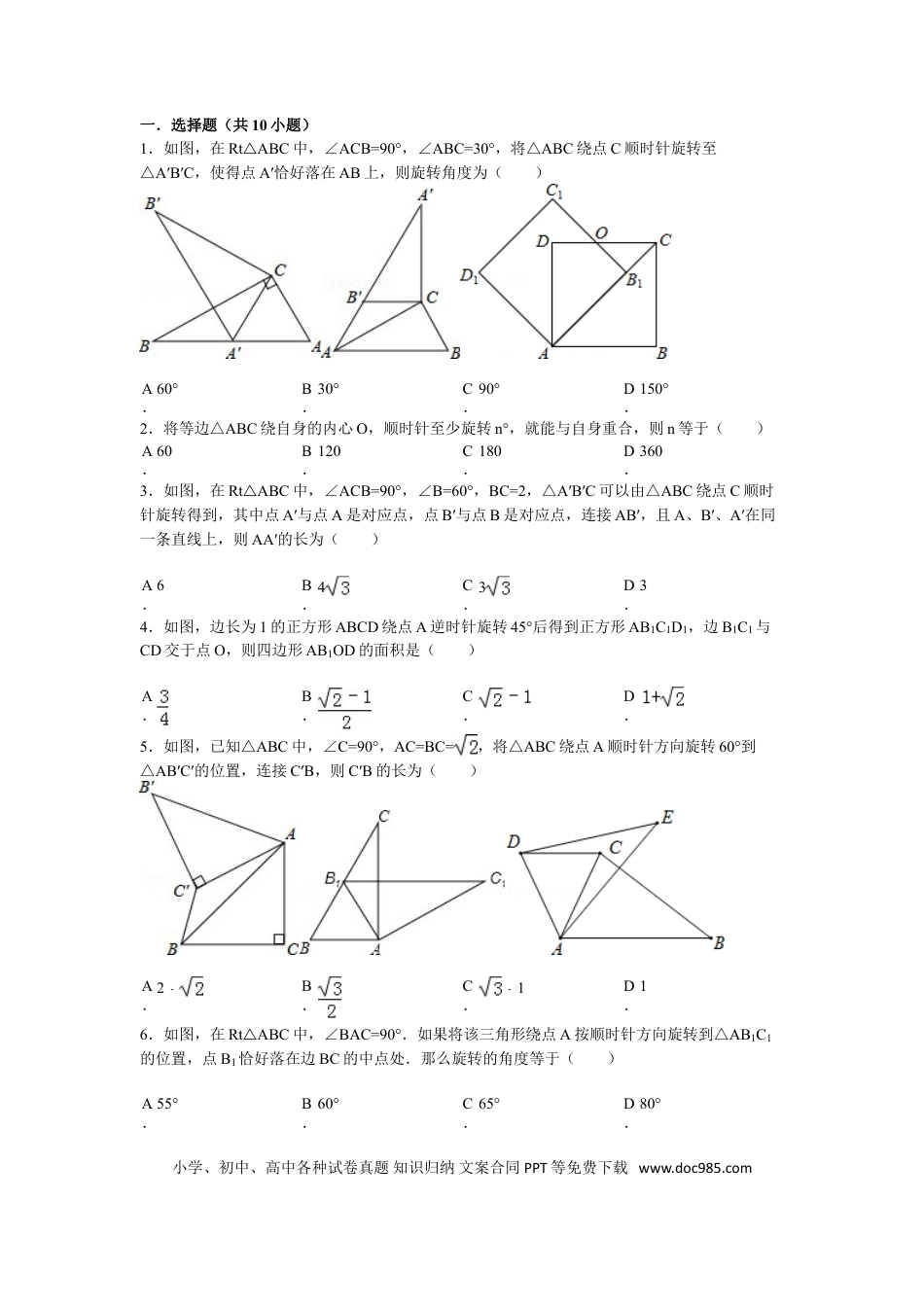
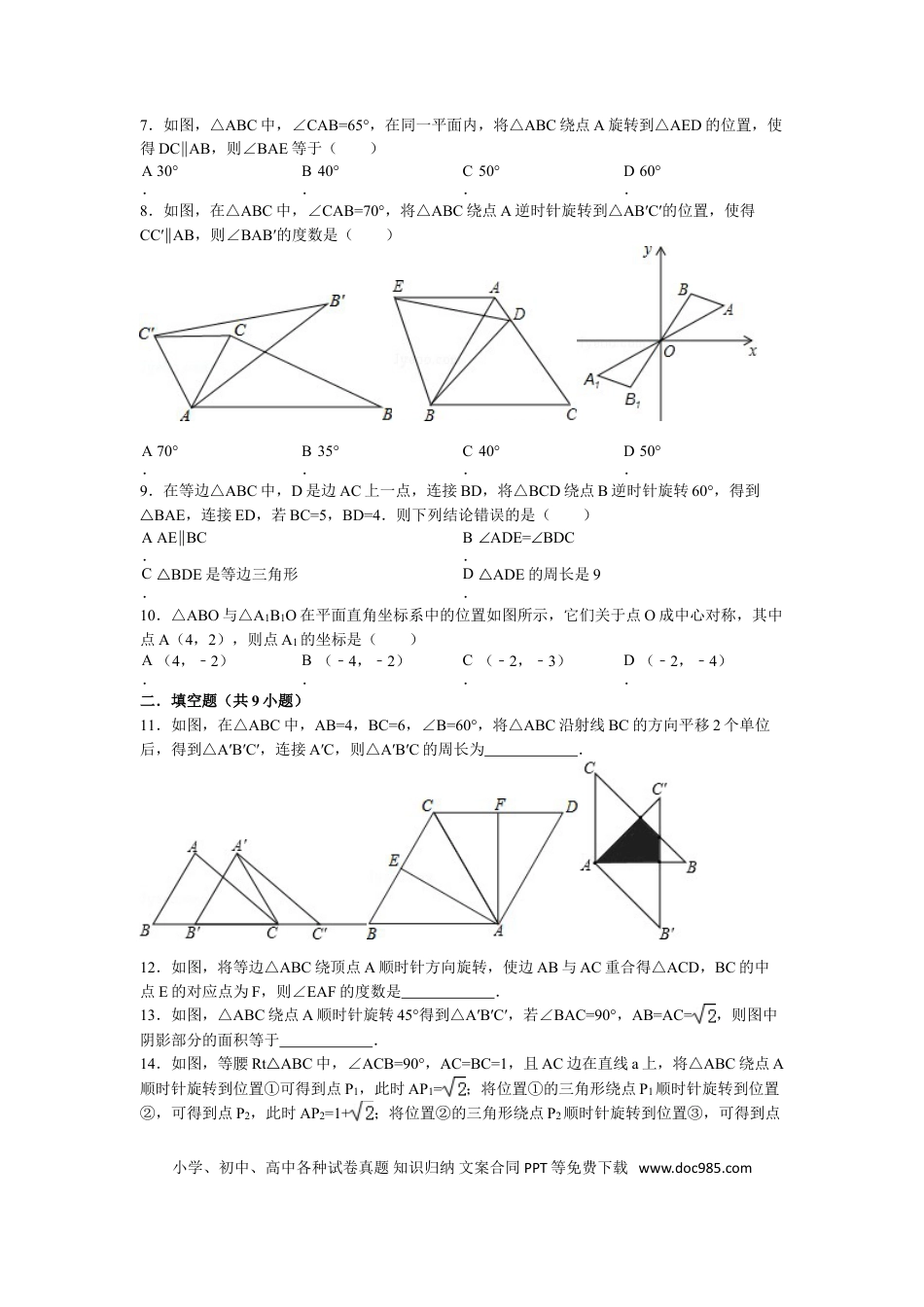
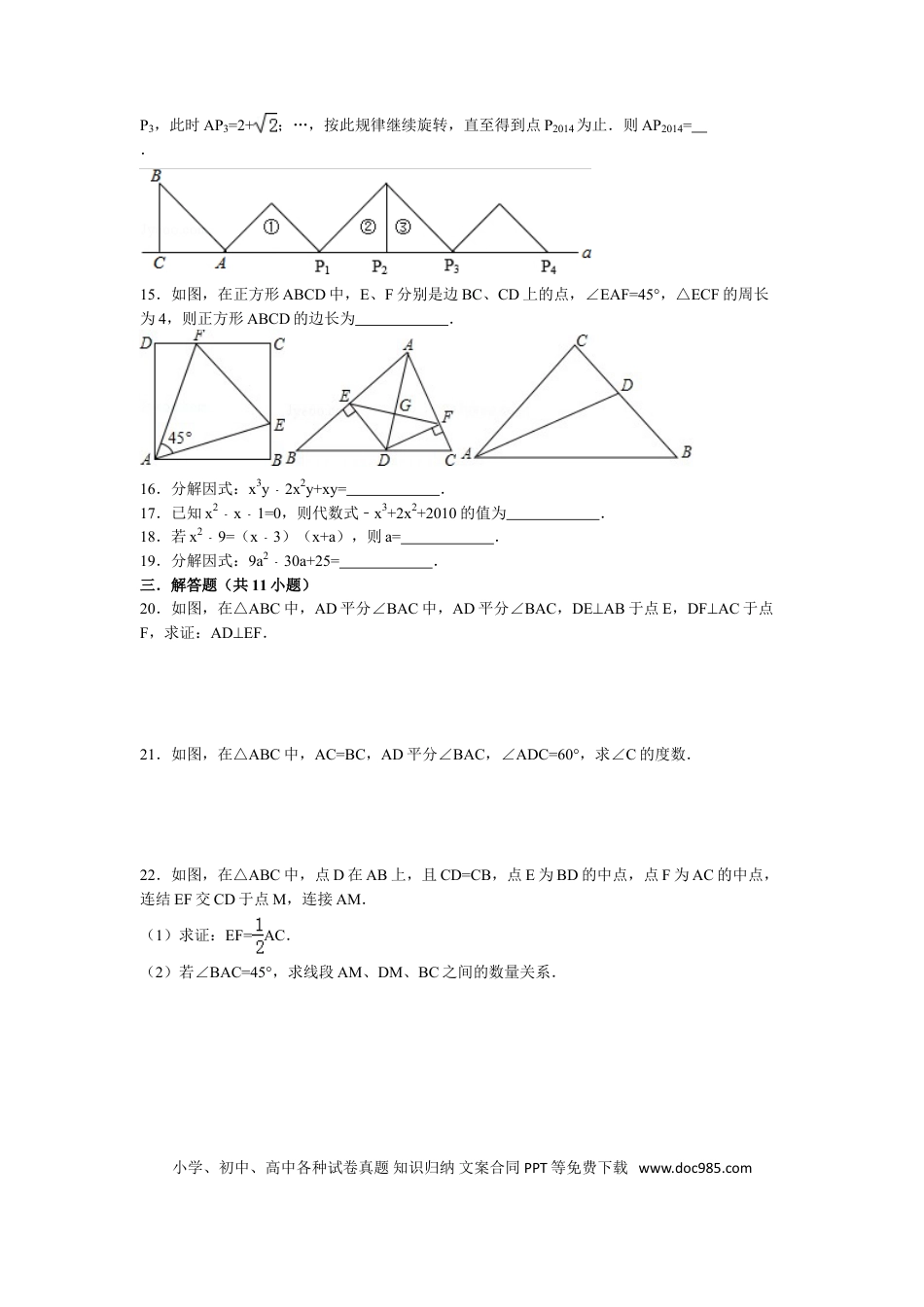
一．选择题（共10小题）1．如图，在RtABC△中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为（）A．60°B．30°C．90°D．150°2．将等边△ABC绕自身的内心O，顺时针至少旋转n°，就能与自身重合，则n等于（）A．60B．120C．180D．3603．如图，在RtABC△中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（）A．6B．4C．3D．34．如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，边B1C1与CD交于点O，则四边形AB1OD的面积是（）A．B．C．D．5．如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为（）A．2﹣B．C．1﹣D．16．如图，在RtABC△中，∠BAC=90°．如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置，点B1恰好落在边BC的中点处．那么旋转的角度等于（）A．55°B．60°C．65°D．80°小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7．如图，△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A旋转到△AED的位置，使得DCAB∥，则∠BAE等于（）A．30°B．40°C．50°D．60°8．如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′AB∥，则∠BAB′的度数是（）A．70°B．35°C．40°D．50°9．在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到BAE△，连接ED，若BC=5，BD=4．则下列结论错误的是（）A．AEBC∥B．ADE=BDC∠∠C．BDE△是等边三角形D．ADE△的周长是910．△ABO与△A1B1O在平面直角坐标系中的位置如图所示，它们关于点O成中心对称，其中点A（4，2），则点A1的坐标是（）A．（4，﹣2）B．（﹣4，﹣2）C．（﹣2，﹣3）D．（﹣2，﹣4）二．填空题（共9小题）11．如图，在△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移2个单位后，得到△A′B′C′，连接A′C，则△A′B′C的周长为．12．如图，将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数是．13．如图，△ABC绕点A顺时针旋转45°得到△A′B′C′，若∠BAC=90°，AB=AC=，则图中阴影部分的面积等于．14．如图，等腰RtABC△中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=1+；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comP3，此时AP3=2+；…，按此规律继续旋转，直至得到点P2014为止．则AP2014=．15．如图，在正方形ABCD中，E、F分别是边BC、CD上的点，∠EAF=45°，△ECF的周长为4，则正方形ABCD的边长为．16．分解因式：x3y2x﹣2y+xy=．17．已知x2x1=0﹣﹣，则代数式﹣x3+2x2+2010的值为．18．若x29=﹣（x3﹣）（x+a），则a=．19．分解因式：9a230a+25=﹣．三．解答题（共11小题）20．如图，在△ABC中，AD平分∠BAC中，AD平分∠BAC，DEAB⊥于点E，DFAC⊥于点F，求证：ADEF⊥．21．如图，在△ABC中，AC=BC，AD平分∠BAC，∠ADC=60°，求∠C的度数．22．如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．（1）求证：EF=AC．（2）若∠BAC=45°，求线段AM、DM、BC之间的数量关系．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com23．如图，请在下列四个等式中，选出两个作为条件，推出△AED是等腰三角形，并予以证明．（写出一种即可）等式：①AB=DC，②BE=CE，③∠B=C∠，④∠BAE=CDE∠．已知：求证：△AED是等腰三角形．证明：24．如图，CD为RtABC△斜边上的高，∠BAC的平分线分别交CD、BC于点E、F．且FGAB⊥，垂足为G，求证：CE=FG．25．（1）如图1，点P是正方形ABCD内的一点，把△ABP绕点B顺时针方向旋转，使点A与点C...