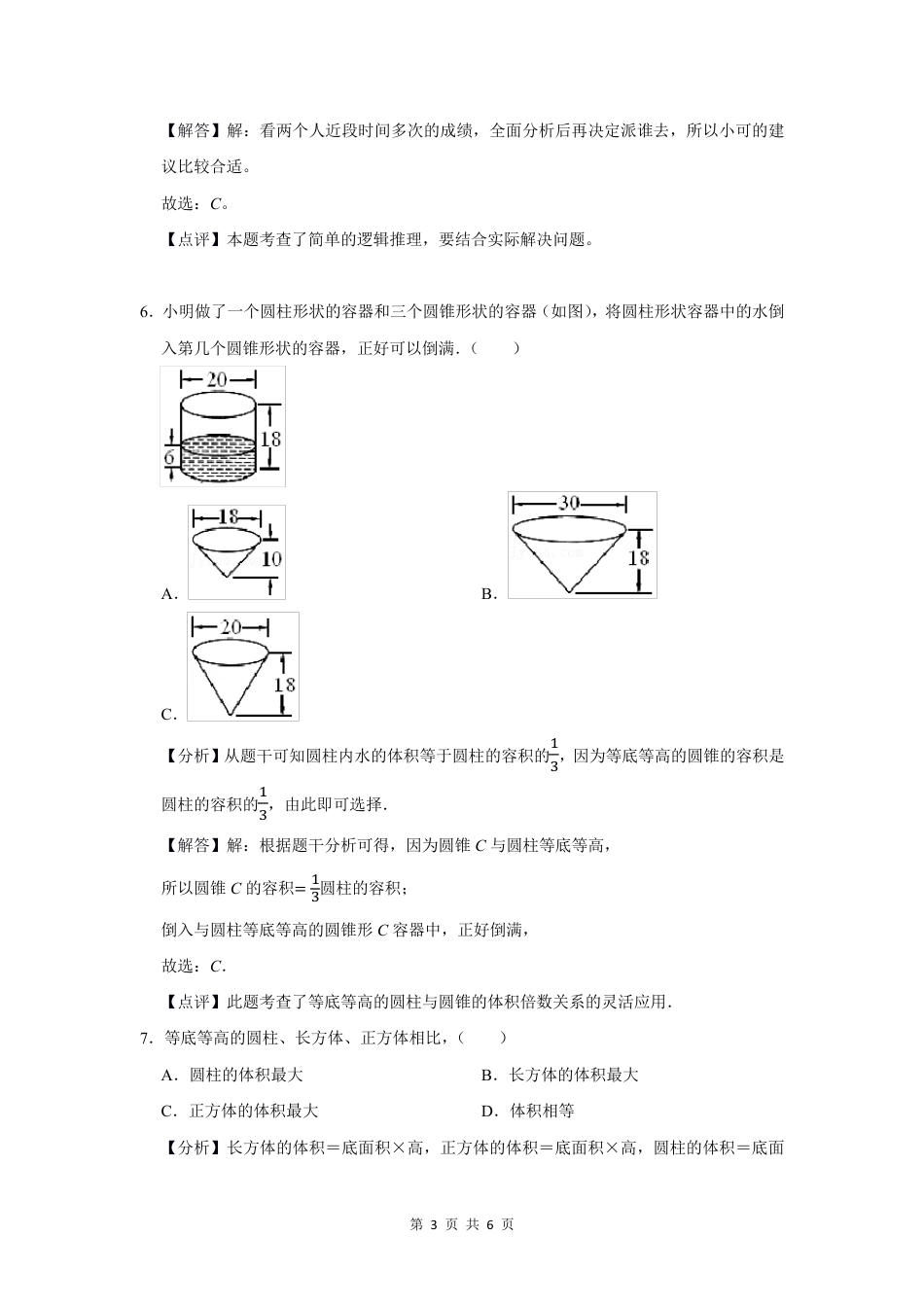
第1页共6页2022年七台河市小升初数学常考题1．在中国象棋比赛中，有8名运动员参加比赛，如果每2名运动员之间都要进行一场比赛，一共要进行（）场比赛。A．28B．14C．20D．8【分析】每两个人之间都要比赛一场，即进行循环赛，共有8人，则每人都要与另外7人进行比赛，每人要参赛7场，8人共参赛8×7＝56（场）；由于比赛是在两人之间进行的，所以一共要进行比赛56÷2＝28（场）；据此解答即可。【解答】解：8×（8﹣1）÷2＝56÷2＝28（场）答：一共要进行28场比赛。故选：A。【点评】循环赛中，参赛人数与比赛场数之间的关系为：参赛人数×（参赛人数﹣1）÷2＝比赛总场数。2．给正方体的6个面涂上3种颜色（每个面涂1种颜色），不论怎么涂，至少有（）个面的颜色相同。A．2B．3C．4D．5【分析】因为正方体有6个面，如果每个面颜色都不相同则需要6种颜色，所以只要是6种以内的颜色都会出现至少2个面颜色相同；给一个正方体6个面分别涂上不同的3种颜色，将3种颜色当做抽屉，将6个面当元素，因为6＞3，根据抽屉原理可知，不管怎么涂至少有两个面涂的颜色相同。【解答】解：给一个正方体6个面分别涂上不同的3种颜色，将4种颜色当做抽屉，将6个面当元素，因为6＞3，根据抽屉原理可知，6÷3＝2（个）即不管怎么涂至少有两个面涂的颜色相同。故选：A。【点评】把多于n个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。第2页共6页3．盒子里有6个黄球，4个红球，每次摸一个，至少摸（）次一定会摸到红球。A．7B．6C．5【分析】考虑最坏情况：摸6次，都是摸出的黄球，则再摸出一个一定是红球；据此即可解答。【解答】解：6+1＝7（次），答：至少摸7次一定会摸到红球．故选：A。【点评】此考查抽屉原理，要注意考虑最差情况。4．5个人坐4把椅子，总有一把椅子上至少坐（）人。A．5B．4C．3D．2【分析】把4把椅子看作4个抽屉；5个人看作5个元素，最差情况是：每把椅子等分的话，每把椅子会坐1人；那还有1个人，随便分给哪把椅子，都会使得一把椅子至少坐2个人。【解答】解：5÷4＝1（人）……1（人）1+1＝2（人）即总有一把椅子上至少坐2人。故选：D。【点评】抽屉原理问题的重点是建立抽屉，关键是在考虑最差情况的基础上得出均分数（商）；然后根据：至少数＝商+1（在有余数的情况下）。5．某学校每年一次的跳绳比赛即将开始了。每班要派出一名同学参加一分钟单人跳绳比赛，班主任张老师了解到班里跳绳成绩突出的是小麦和小田，派谁去呢？下面几位同学想到的方法，你认为（）的方法比较合适。A．小西：两人各跳一次，谁的成绩好就派谁去B．小阳：看两个人的最好成绩，谁的高就派谁去C．小可：看两个人近段时间多次的成绩，全面分析后再决定派谁去【分析】班主任张老师了解到班里跳绳成绩突出的是小麦和小田，所以要从这两个人里面选择派谁去，要结合近段时间多次的成绩，选择稳定且成绩好的同学去，据此解答即可。第3页共6页【解答】解：看两个人近段时间多次的成绩，全面分析后再决定派谁去，所以小可的建议比较合适。故选：C。【点评】本题考查了简单的逻辑推理，要结合实际解决问题。6．小明做了一个圆柱形状的容器和三个圆锥形状的容器（如图），将圆柱形状容器中的水倒入第几个圆锥形状的容器，正好可以倒满．（）A．B．C．【分析】从题干可知圆柱内水的体积等于圆柱的容积的13，因为等底等高的圆锥的容积是圆柱的容积的13，由此即可选择．【解答】解：根据题干分析可得，因为圆锥C与圆柱等底等高，所以圆锥C的容积=13圆柱的容积；倒入与圆柱等底等高的圆锥形C容器中，正好倒满，故选：C．【点评】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用．7．等底等高的圆柱、长方体、正方体相比，（）A．圆柱的体积最大B．长方体的体积最大C．正方体的体积最大D．体积相等【分析】长方体的体积＝底面积×高，正方体的体积＝底面积×高，圆柱的体积＝底面第4页共6页方体、长方体和圆柱体的底面积和高都分别相等，那么的体积也相等．【解答】解：因为：长方体的体积＝底面积×高，圆柱的体积＝底面积×高，正方体的体积＝底面积×高；所以，等底等高的正方体、长方体和圆柱的...