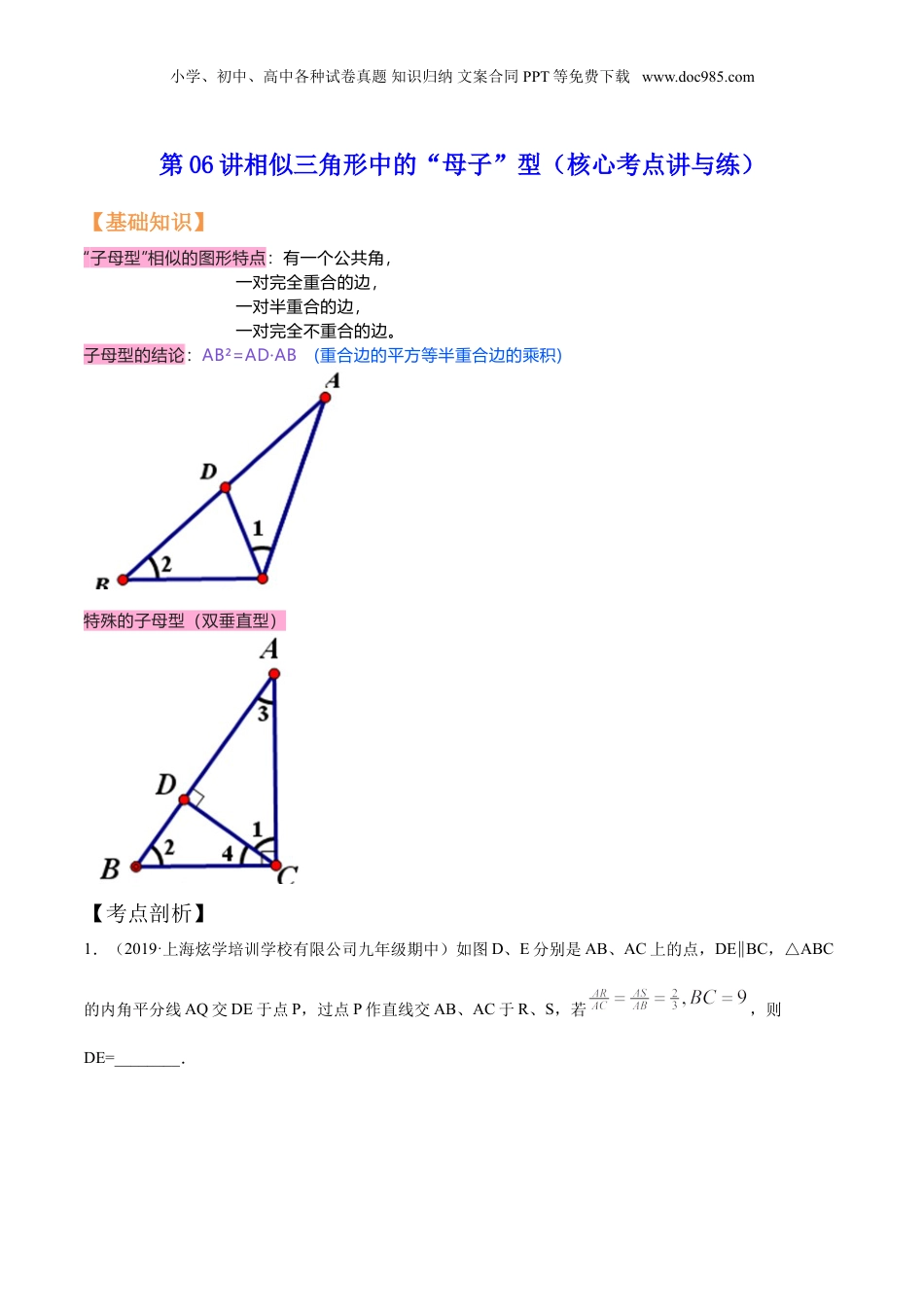
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第06讲相似三角形中的“母子”型（核心考点讲与练）【基础知识】“子母型”相似的图形特点：有一个公共角，一对完全重合的边，一对半重合的边，一对完全不重合的边。子母型的结论：AB²=AD·AB(重合边的平方等半重合边的乘积)特殊的子母型（双垂直型）【考点剖析】1．（2019·上海炫学培训学校有限公司九年级期中）如图D、E分别是AB、AC上的点，DEBC∥，△ABC的内角平分线AQ交DE于点P，过点P作直线交AB、AC于R、S，若，则DE=________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】6【分析】由，且∠RAS=CAB∠，可证得△ARSACB△∽，所以∠ARS=ACB∠，再由∠BAP=CAQ可证得△ARPACQ∽△，，再由DEBC∥，可知，把BC的值代入可求得DE．【详解】解： ，且∠RAS=CAB∠，ARSACB∴△△，ARS=ACB∴∠∠，又 AQ为角平分线，BAP=CAQ∴∠，ARPACQ∴△△∽，∴，DEBC∥ ，∴，BC=9 ，∴，DE=6∴．【点睛】本题主要考查三角形相似的判定和性质，解题的关键是能利用条件两次证得三角形相似，从而得到DE和BC的比值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2018·上海市西南模范中学九年级阶段练习）已知，平行四边形中，点是的中点，在直线上截取，连接，交于，则___________．【答案】；．【分析】由于F的位置不确定，需分情况进行讨论，（1）当点F在线段AD上时（2）点F在AD的延长线上时两种情况，然后通过证两三角形相似从而得到AG和CG的比，进一步得到AG和AC的比．【详解】解：（1）点F在线段AD上时，设EF与CD的延长线交于H，AB//CD ，EAFHDF,∴△△∽HD∴：AE=DF：AF=1:2，即HD=AE，AB//CD ，CHGAEG∴△△∽，AG∴：CG=AE：CH，AB=CD=2AE ，CH=CD+DH=2AE+∴AE=AE，AG∴：CG=2：5，AG∴：（AG+CG）=2：（2+5），即AG：AC=2：7；（2）点F在线段AD的延长线上时，设EF与CD交于H，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comAB//CD ，EAFHDF∴△△∽，HD∴：AE=DF：AF=1：2，即HD=AE，AB//CD ，AG∴：CG=AE：CHAB=CD=2AE ，CH=CD-DH=2AE-∴AE=AE，AG∴：CG=2：3，AG∴：（AG+CG）=2：（2+3），即AG：AC=2：5．故答案为：或．【点睛】本题考查相似三角形的性质以及分类讨论的数学思想；其中相似三角形的性质得出的比例式是解题关键，特别注意：求相似比不仅要认准对应边，还需注意两个三角形的先后次序．二、解答题3．（2019·上海市育才初级中学九年级阶段练习）已知：如图所示，中，CD⊥AB，，BD=1，AD=4，求AC的长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】【分析】根据题意由锐角三角函数可求∠A=BCD∠，可证△ACDCBD∽△，即可求CD的长，由勾股定理即可求出AC的长．【详解】解： CDAB⊥，∴且，sinA=sinBCD∴∠∠，A=BCD∴∠∠，且∠ADC=BDC=90°∠，ACDCBD∴△△∽∴，CD∴2=BD•AD=4CD=2∴，∴．【点睛】本题考查相似三角形的判定和性质以及锐角三角函数的定义，根据题意求出CD的长是解答本题的关键．4．（2021·上海黄浦·九年级期中）直线分别交x轴、y轴于A、B两点．（1）求出点A、B的坐标；（2）已知点G的坐标为（2，7），过点G和B作直线BG，连接AG，求∠AGB的正切值；（3）在（2）的条件下，在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△AOB相似？若存在，请求出点Q的坐标；若不存在，请说明理由．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】（1），；（2）；（3）存在，，，，【分析】（1）对于，令x＝0，则y＝1，令y＝0，即＝0，解得x＝3，即可求解；（2）证明AG2＝AB2＋BG2，则△ABG为直角三角形，即可求解；（3）分△ABQ∽△AOB、△ABQ∽△BOA两种情况，利用三角形相似边的比例关系，即可求解．【详解】解：（1）对于，令x＝0，则y＝1，令y＝0，即＝0，解得x＝3，故点A、B的坐标分别（3，0）、（0，1）；（2）由A、B、G的坐标知，BG2＝22＋（7−1）2＝40，同理AB2＝10，AG2＝50，故AG...