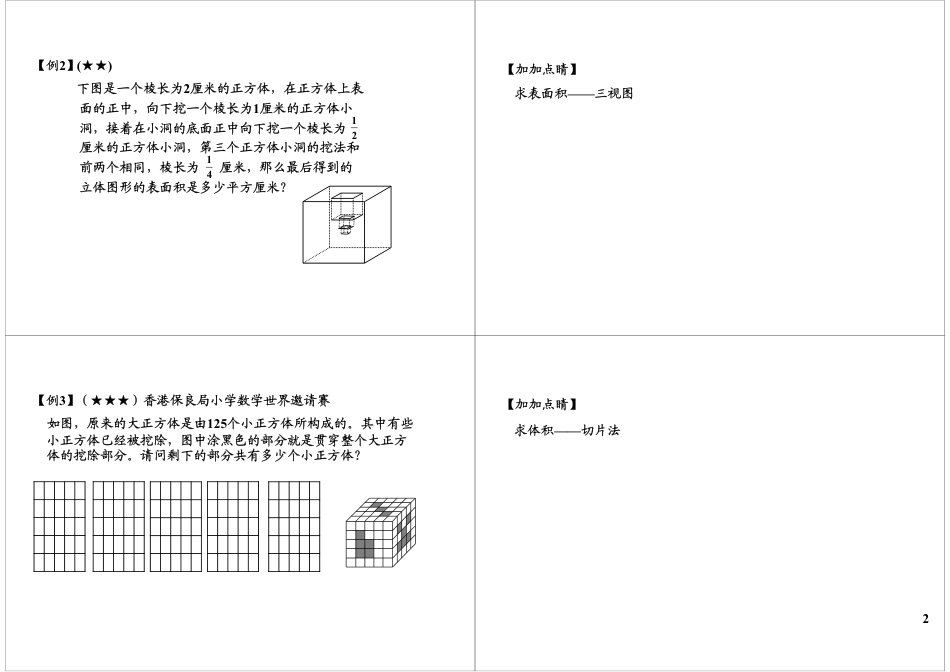
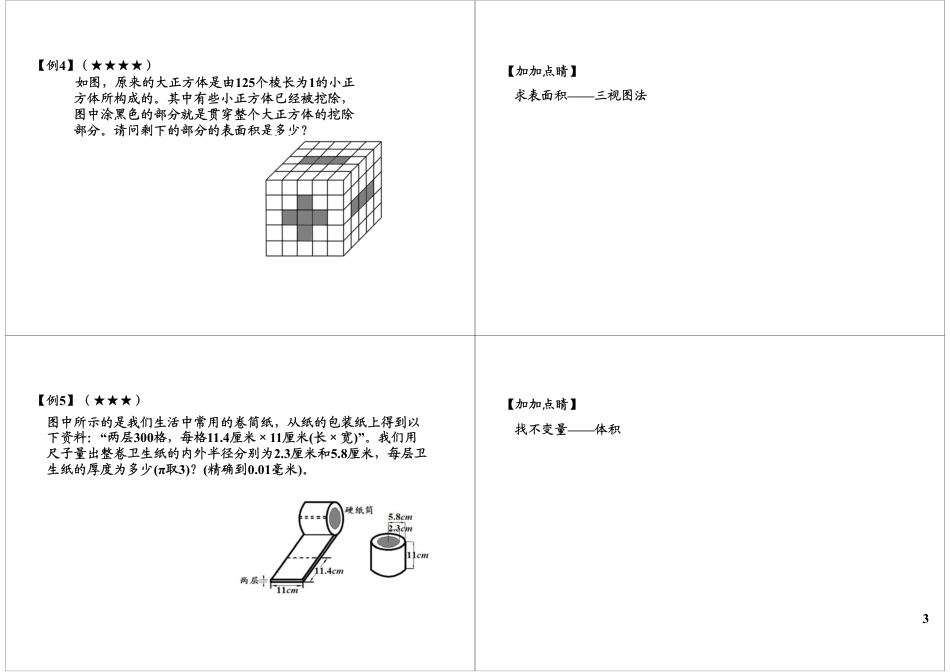
1．直线型立体几何：⑴长方体的表面积和体积的计算公式正方体是各棱相等的长方体，它是长方体的特例，它的六个面都是正方形。如果它的棱长为a，那么：2()Sabbcca长方体表面积：；Vabc。长方体体积：26Sa，正方体3Va。正方体加油站立体几何常用技巧⑵由小立方体堆砌而成的立体图形，其表面积可用三视图法求解：⑶水中浸物问题的水面高度公式：(+++)2S正视图面积俯视图面积侧视图面积凹槽数=VVhS水铁块水容器完全没过时：；=VhSS水水容器铁块部分没过时：；=hh水容器水溢出时：2．曲线型立体几何：圆柱与圆锥的体积公式分别是2Vrh、213Vrh。【例1】（★★）走美6年级试题21个棱长为1厘米的小正方体组成一个立体如下图，它的表面积是______平方厘米。1【例2】(★★)下图是一个棱长为2厘米的正方体，在正方体上表面的正中，向下挖一个棱长为1厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为厘米的正方体小洞，第三个正方体小洞的挖法和前两个相同，棱长为厘米，那么最后得到的立体图形的表面积是多少平方厘米？1214【加加点睛】求表面积——三视图【例3】（★★★）香港保良局小学数学世界邀请赛如图，原来的大正方体是由125个小正方体所构成的。其中有些小正方体已经被挖除，图中涂黑色的部分就是贯穿整个大正方体的挖除部分。请问剩下的部分共有多少个小正方体？【加加点睛】求体积——切片法2【例4】（★★★★）如图，原来的大正方体是由125个棱长为1的小正方体所构成的。其中有些小正方体已经被挖除，图中涂黑色的部分就是贯穿整个大正方体的挖除部分。请问剩下的部分的表面积是多少？【加加点睛】求表面积——三视图法【例5】（★★★）图中所示的是我们生活中常用的卷筒纸，从纸的包装纸上得到以下资料：“两层300格，每格11.4厘米×11厘米(长×宽)”。我们用尺子量出整卷卫生纸的内外半径分别为2.3厘米和5.8厘米，每层卫生纸的厚度为多少(π取3)？(精确到0.01毫米)。【加加点睛】找不变量——体积3【例6】(★★★★)如图，一个底面长30分米，宽10分米，高12分米的长方体水池，存有四分之三水，请问：⑴将一个高11分米，体积330立方分米的圆柱放入水池，水面的高度为多少分米？⑵如果再放入一个同样的圆柱，水面高度又变成了多少分米？⑶如果再放入一个同样的圆柱，水面高度又变成了多少分米？【加加点睛】=VVhS水铁块水容器完全没过时：；=VhSS水水容器铁块部分没过时：；=hh水容器水溢出时：【例7】（★★★★）如图若以长方形的一条宽AB为轴旋转一周后，甲乙两部分所成的立体图形的体积比是多少？AB【例8】（★★★★★）华杯赛决赛试题如图，ABCD是矩形，BC=6cm，AB=10cm，对角线AC、BD相交O。图中的阴影部分以CD为轴旋转一周，则阴影部分扫出的立体的体积是多少立方厘米？(取3)πDCBAO4【加加点睛】2Vrh、圆柱：213Vrh。圆锥：【本讲总结】长方体：体积：切片法；表面积：三视图旋转体体积：重要思想：寻找不变量重点例题：例3，例4，例5，例82Vrh、圆柱：213Vrh。圆锥：5