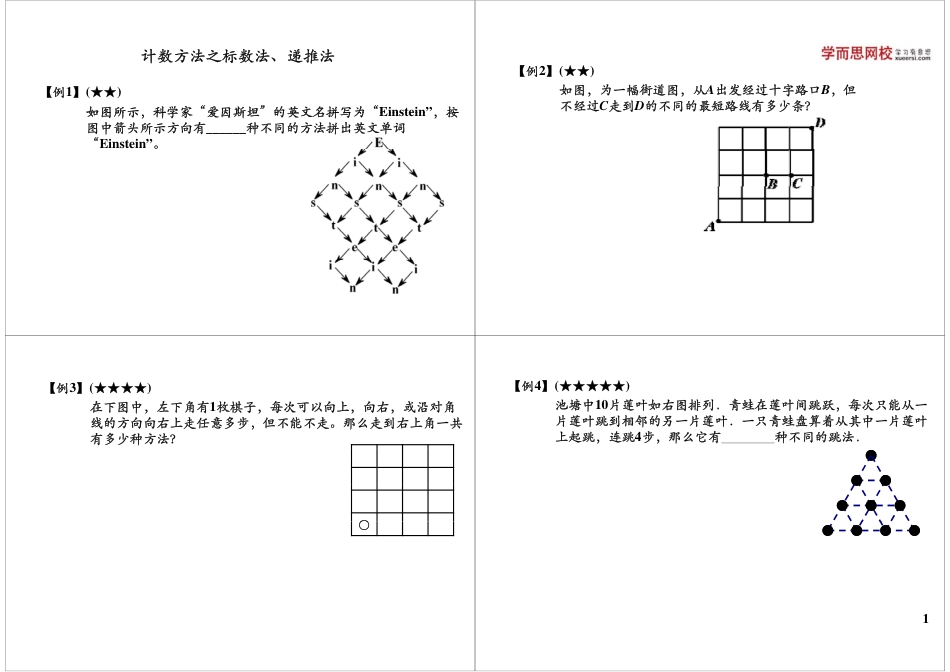
计数方法之标数法、递推法【例1】(★★)如图所示科学家“爱因斯坦”的英文名拼写为“Einstein”按如图所示，科学家爱因斯坦的英文名拼写为Einstein，按图中箭头所示方向有______种不同的方法拼出英文单词“Einstein”。【例2】(★★)【例】()如图，为一幅街道图，从A出发经过十字路口B，但不经过C走到D的不同的最短路线有多少条？【例3】(★★★★)在下图中，左下角有1枚棋子，每次可以向上，向右，或沿对角在下图中，左下角有枚棋子，每次可以向上，向右，或沿对角线的方向向右上走任意多步，但不能不走。那么走到右上角一共有多少种方法？○【例4】(★★★★★)池塘中10片莲叶如右图排列．青蛙在莲叶间跳跃，每次只能从一中，片莲叶跳到相邻的另一片莲叶．一只青蛙盘算着从其中一片莲叶上起跳，连跳4步，那么它有种不同的跳法．1【例5】(★★★★★)游乐园门票1元1张，每人限购1张.现有10个小朋友排队购买，其中5个小朋友只有1元的钞票，另外5个小朋友只有2元的钞票，售票员没有零钱。10个小朋友排队，不同的排队方法总共有10！3628800种问其中有种排队方法售票员总能找的开＝3628800种，问其中有______种排队方法，售票员总能找的开零钱。【例6】(★★★)如下图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？BA【例7】(★★★)【例7】(★★★)一个楼梯共有12级台阶，规定每步可以迈1级台阶或2级台阶，最多可以迈3级台阶从地面到最上面1级台阶一共可以有多少种多可以迈3级台阶，从地面到最上面1级台阶，一共可以有多少种不同的走法？【例8】(★★★)在平面上画8个圆，最多可以把平面分成_______部分。【例9】(★★★★)个长方形把平面分成两部分那么10个长方形最多把平面分成一个长方形把平面分成两部分，那么10个长方形最多把平面分成_______部分.①标数法与递推法都是加法原理本讲总结①标数法与递推法都是加法原理②按最后一步进行分类，做加法③标数时要注意限制条件④分平面问题要确定交点个数④平要确点个重点例题：例3、例4、例5、例7、例82