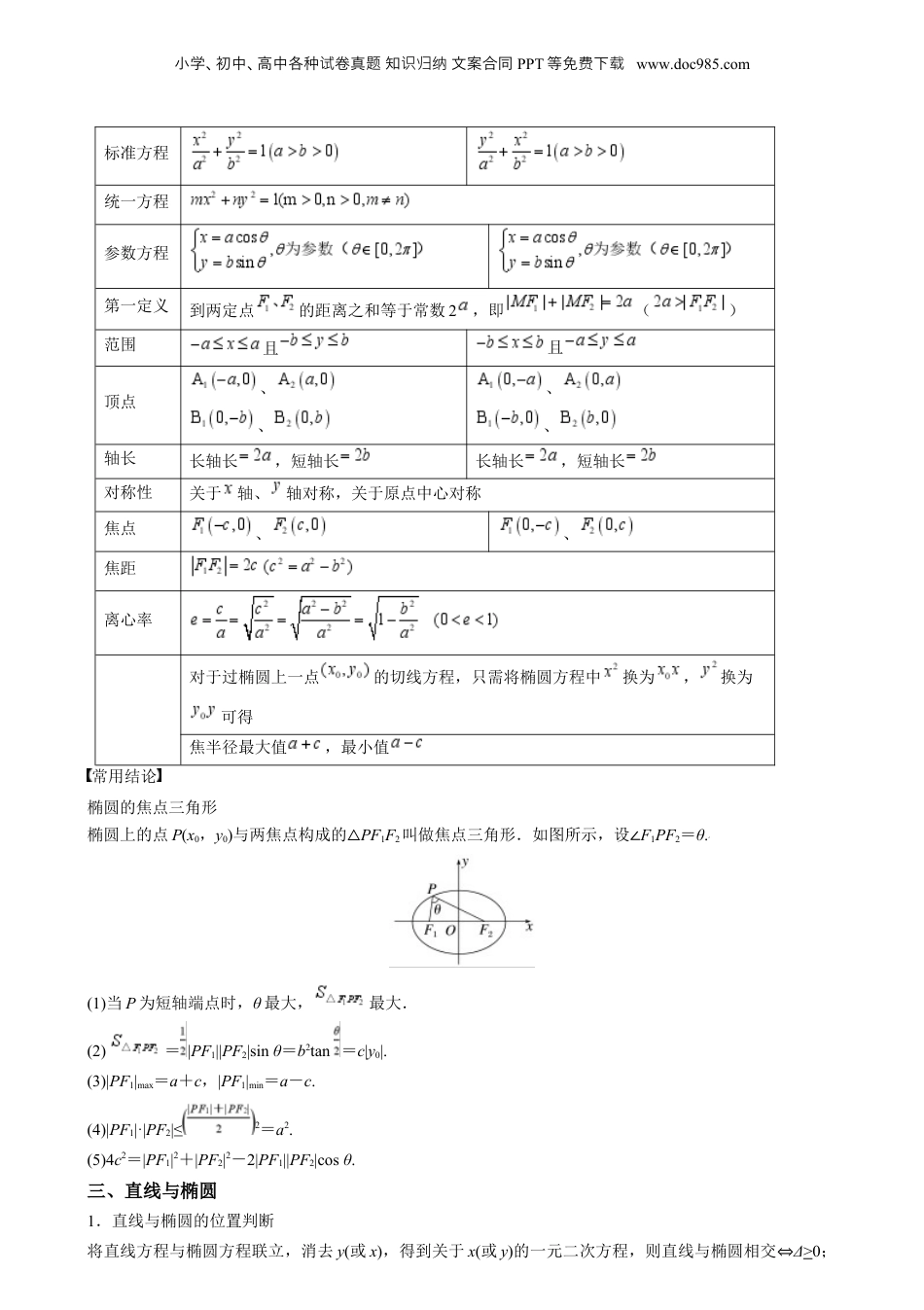
小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com专题25椭圆目录01思维导图02知识清单03核心素养分析04方法归纳一、椭圆平面内与两个定点的距离之和等于常数（）的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距，记作，定义用集合语言表示为：注意：当时，点的轨迹是线段；当时，点的轨迹不存在．二、椭圆的性质焦点的位置焦点在轴上焦点在轴上图形小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com标准方程统一方程参数方程第一定义到两定点的距离之和等于常数2，即（）范围且且顶点、、、、轴长长轴长，短轴长长轴长，短轴长对称性关于轴、轴对称，关于原点中心对称焦点、、焦距离心率对于过椭圆上一点的切线方程，只需将椭圆方程中换为，换为可得焦半径最大值，最小值常用结论椭圆的焦点三角形椭圆上的点P(x0，y0)与两焦点构成的△PF1F2叫做焦点三角形．如图所示，设∠F1PF2＝θ.(1)当P为短轴端点时，θ最大，最大．(2)＝|PF1||PF2|sinθ＝b2tan＝c|y0|.(3)|PF1|max＝a＋c，|PF1|min＝a－c.(4)|PF1|·|PF2|≤2＝a2.(5)4c2＝|PF1|2＋|PF2|2－2|PF1||PF2|cosθ.三、直线与椭圆1．直线与椭圆的位置判断将直线方程与椭圆方程联立，消去y(或x)，得到关于x(或y)的一元二次方程，则直线与椭圆相交⇔Δ>0；小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com直线与椭圆相切⇔Δ＝0；直线与椭圆相离⇔Δ<0.2．弦长公式设直线与椭圆的交点坐标为A(x1，y1)，B(x2，y2)，则|AB|＝|x1－x2|＝或|AB|＝|y1－y2|＝，k为直线斜率且k≠0.常用结论已知椭圆＋＝1(a＞b＞0)．(1)通径的长度为.(2)过左焦点的弦AB，A(x1，y1)，B(x2，y2)，则焦点弦|AB|＝2a＋e(x1＋x2)；过右焦点弦CD，C(x3，y3)，D(x4，y4)，则焦点弦|CD|＝2a－e(x3＋x4)．(e为椭圆的离心率)(3)A1，A2为椭圆的长轴顶点，P是椭圆上异于A1，A2的任一点，则.(4)AB是椭圆的不平行于对称轴的弦，O为原点，M为AB的中点，则kOM·kAB＝－.(5)过原点的直线交椭圆于A，B两点，P是椭圆上异于A，B的任一点，则kPA·kPB＝－.(6)点P(x0，y0)在椭圆上，过点P的切线方程为＋＝1.椭圆是高考考查的重点和热点，其中椭圆的方程、几何性质等常以选择题、填空题形式出现；直线与椭圆的综合问题如弦长问题等常常以解答题形式出现。Ⅰ、椭圆及其性质题型一椭圆的定义及其应用例1设定点，，动点满足条件，则点的轨迹是（）A．椭圆B．线段C．射线D．椭圆或线段【答案】D【分析】利用基本不等式求出的范围，根据椭圆的定义可得答案.【解析】因为，所以，当且仅当时等号成立，当时，，而，此时点的轨迹是线段；当时，，小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com此时点的轨迹是以、为焦点的椭圆．综上所述，点的轨迹是以、为焦点的椭圆或线段.故选：D.方法归纳：椭圆定义的应用技巧(1)椭圆定义的应用主要有：求椭圆的标准方程、求焦点三角形的周长、面积及求弦长、最值和离心率等．(2)通常将定义和余弦定理结合使用求解关于焦点三角形的周长和面积问题．题型二椭圆的标准方程命题点1定义法例2已知椭圆的两个焦点坐标分别是，椭圆上一点到两个焦点的距离之和为26，则该椭圆方程为.【答案】【分析】根据已知条件及椭圆定义求椭圆的标准方程.【解析】由题意，椭圆的两个焦点坐标分别是，则椭圆的焦点在y轴上，且，又椭圆上一点到两个焦点的距离之和为26，所以，即，所以，所以该椭圆方程为.故答案为：命题点2待定系数法例3已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P1(，1)，P2(－，－)，则该椭圆的方程为________．答案＋＝1解析设椭圆的方程为mx2＋ny2＝1(m>0，n>0，且m≠n)．因为椭圆经过P1，P2两点，所以点P1，P2的坐标满足椭圆方程，则Error!解得Error!所以所求椭圆的方程为＋＝1.方法归纳：根据条件求椭圆方程的主要方法(1)定义法：根据题目所给条件确定动点的轨迹满足椭圆的定义．(2)待定系数法：根据题目所给的条件确定椭圆中的a，b.当不知焦点在哪一个坐标轴上时，一般可设所求椭圆的方程为mx2＋ny2＝1(m>0，...