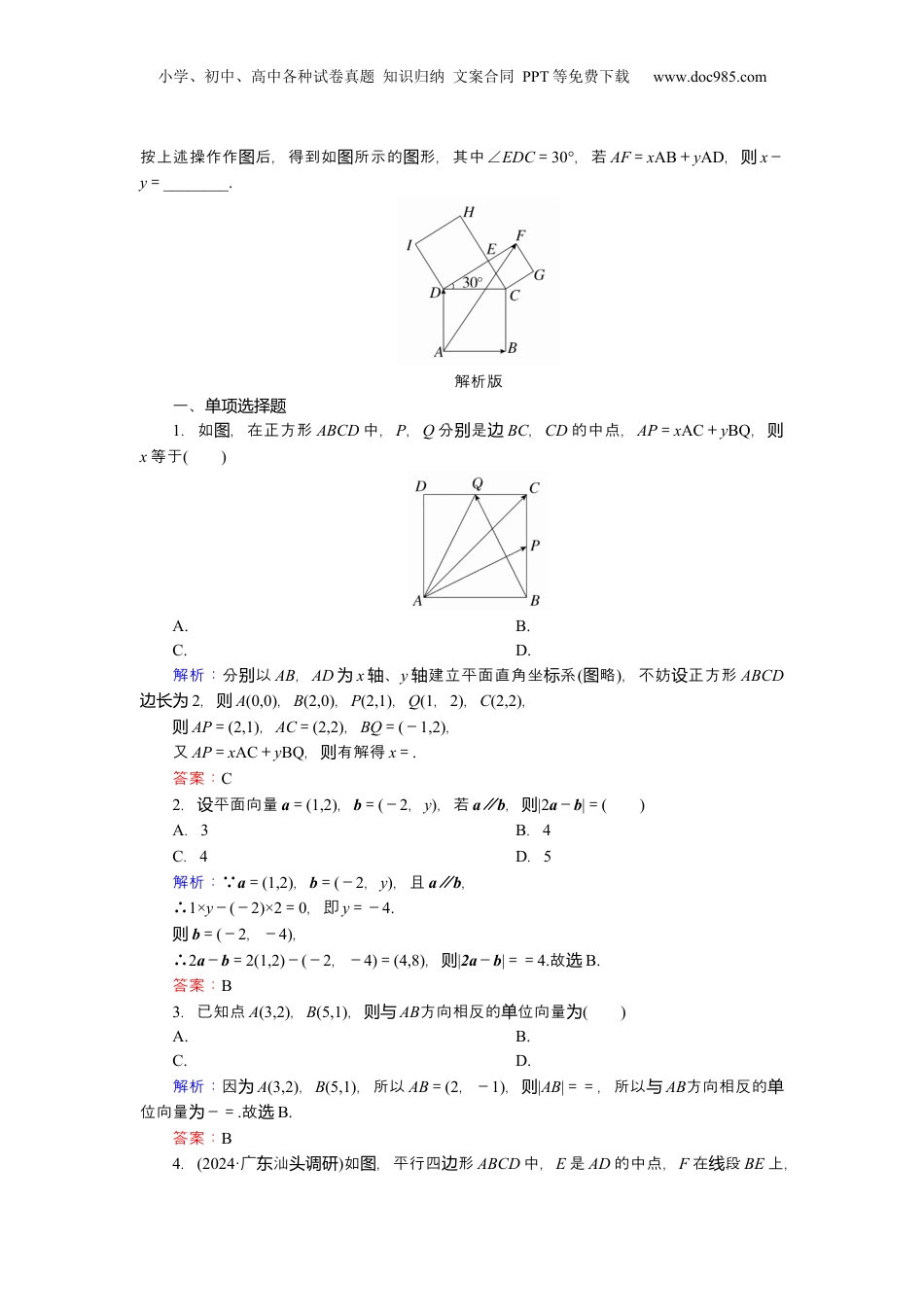
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com限跟踪时检测(三十二)平面向量基本定理及坐表示标一、单项选择题1．如，在正方形图ABCD中，P，Q分是别边BC，CD的中点，AP＝xAC＋yBQ，则x等于()A.B.C.D.2．平面向量设a＝(1,2)，b＝(－2，y)，若a∥b，则|2a－b|＝()A．3B．4C．4D．53．已知点A(3,2)，B(5,1)，则与AB方向相反的位向量单为()A.B.C.D.4．(2024·广汕东头调研)如，平行四形图边ABCD中，E是AD的中点，F在段线BE上，且BF＝3FE，记a＝BA，b＝BC，则CF＝()A.a＋bB.a－bC．－a＋bD.a－b5．(2024·河北衡水中学调研)已知向量a＝，b＝(cosα，1)，α∈，且a∥b，则sin＝()A．－B.C.D．－6．(2024·云南大理模拟)在△ABC中，D是直线AB上的点．若2BD＝CB＋λCA，记△ACB的面积为S1，△ACD的面积为S2，等于则()A.B.C.D.7．(2024·福建泉州模拟)在平面直角坐系中，点标O(0,0)，P(6,8)，向量将OP点绕O按逆方向旋后得向量时针转OQ，点则Q的坐是标()A．(－7，－)B．(－7，)C．(－4，－2)D．(－4，2)二、多项选择题8．若k1a＋k2b＝0，则k1＝k2＝0，那下列么对a，b的判不正确的是断()A．a与b一定共线B．a与b一定不共线小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．a与b一定垂直D．a与b中至少有一个为09．已知向量OA＝(1，－3)，OB＝(2，－1)，OC＝(m＋1，m－2)，若点A，B，C能构成三角形，则实数m可以是()A．－2B.C．1D．－1三、空解答填题与题10．如图1，蜜蜂蜂房是由格的正六柱成的，的一端是平整的六形口．严棱构它边开六形口可边开记为图2中的正六形边ABCDEF，其中O正六形为边ABCDEF的中心，设AB＝a，AF＝b，若BM＝MC，EF＝3EN，则MN＝________.(用a，b表示)图1图211．若{α，β}是一基底，向量个γ＝xα＋yβ(x，y∈R)，则称(x，y)向量为γ在基底{α，β}下的坐，已知向量标现a在基底{p＝(1，－1)，q＝(2,1)}下的坐标为(－2,2)，则a在基底{m＝(－1,1)，n＝(1,2)}下的坐标为________．12．(2024·江常州模苏拟)在△ABC中，C＝45°，O是△ABC的外心，若OC＝mOA＋nOB(m，n∈R)，则m＋n的取范是值围________.13．已知A(－2,4)，B(3，－1)，C(－3，－4)．设AB＝a，BC＝b，CA＝c，且CM＝3c，CN＝－2b.(1)求3a＋b－3c；(2)求足满a＝mb＋nc的实数m，n；(3)求M，N的坐及向量标MN的坐．标14．已知△ABC中，重心过G的直交线边AB于点P，交边AC于点Q，设△APQ的面积为S1，△ABC的面积为S2，AP＝pPB，AQ＝qQC.(1)求的；值(2)求的取范．值围高分推荐题15．根据哥拉斯定理，得到：以直角三角形的三作正方形，斜毕达结论条边为边长从上作出的正方形的面正好等于在直角上作出的正方形面之和．在边积两边积现对Rt△CDE小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com按上述操作作后，得到如所示的形，其中图图图∠EDC＝30°，若AF＝xAB＋yAD，则x－y＝________.解析版一、单项选择题1．如，在正方形图ABCD中，P，Q分是别边BC，CD的中点，AP＝xAC＋yBQ，则x等于()A.B.C.D.解析：分以别AB，AD为x、轴y建立平面直角坐系轴标(略图)，不妨正方形设ABCD边长为2，则A(0,0)，B(2,0)，P(2,1)，Q(1，2)，C(2,2)，则AP＝(2,1)，AC＝(2,2)，BQ＝(－1,2)，又AP＝xAC＋yBQ，有解得则x＝.答案：C2．平面向量设a＝(1,2)，b＝(－2，y)，若a∥b，则|2a－b|＝()A．3B．4C．4D．5解析： a＝(1,2)，b＝(－2，y)，且a∥b，∴1×y－(－2)×2＝0，即y＝－4.则b＝(－2，－4)，∴2a－b＝2(1,2)－(－2，－4)＝(4,8)，则|2a－b|＝＝4.故选B.答案：B3．已知点A(3,2)，B(5,1)，则与AB方向相反的位向量单为()A.B.C.D.解析：因为A(3,2)，B(5,1)，所以AB＝(2，－1)，则|AB|＝＝，所以与AB方向相反的单位向量－＝为.故选B.答案：B4．(2024·广汕东头调研)如，平行四形图边ABCD中，E是AD的中点，F在段线BE上，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com且BF＝3FE，记a＝BA，b＝BC，则CF＝()A.a＋bB.a－bC．－a＋bD.a－b解析：取a＝BA，b＝BC作基底，为则BE＝a＋b.因为BF＝3FE，所以BF＝BE＝＝a＋b，所以CF＝BF－BC＝a...