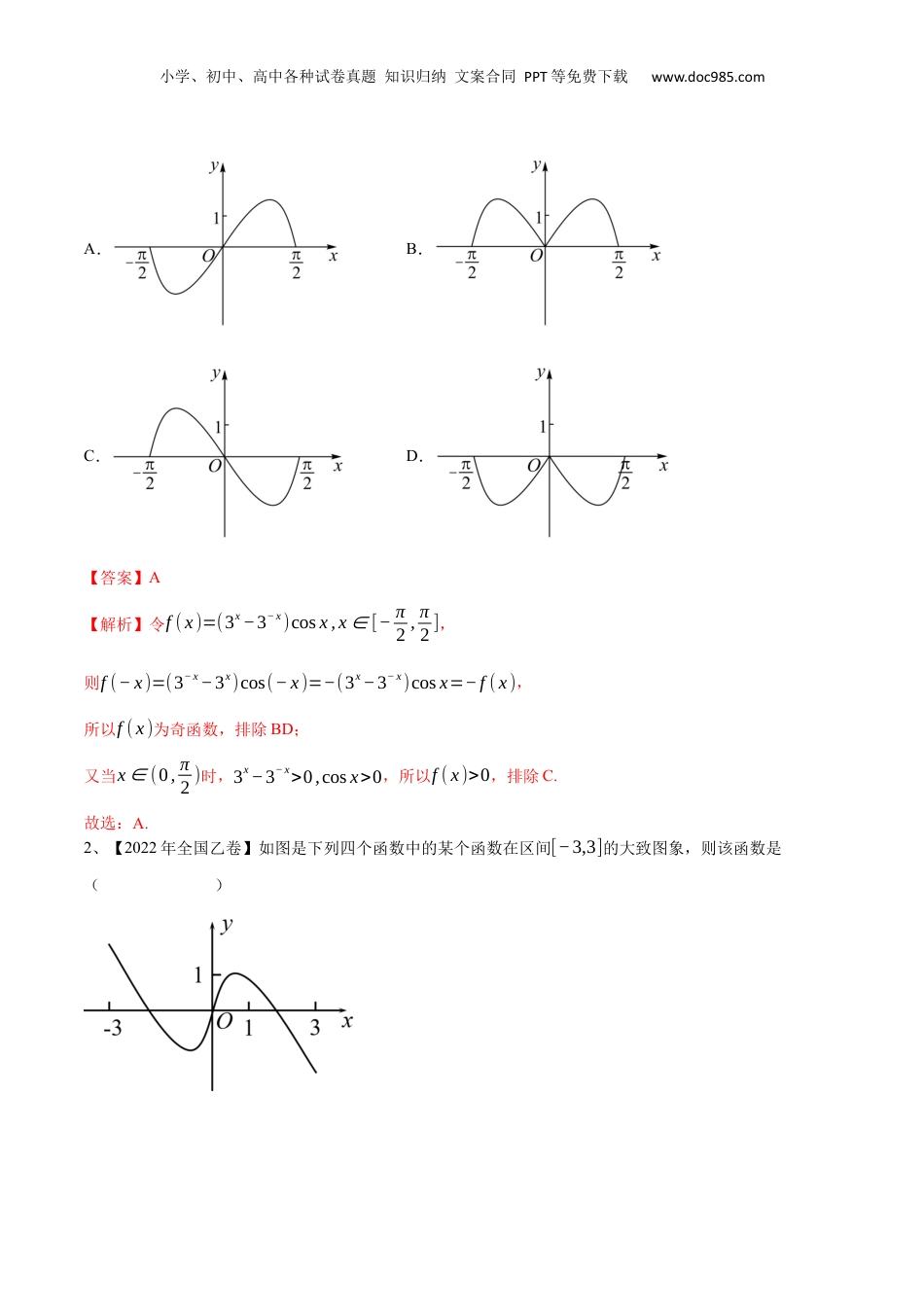
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第14讲函数的图象1.利用描点法作函数的图象步骤：(1)确定函数的定义域；(2)化简函数解析式；(3)讨论函数的性质(奇偶性、单调性、周期性、对称性等)；(4)列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等)，描点，连线.2.利用图象变换法作函数的图象(1)平移变换(2)对称变换y＝f(x)的图象――――――→y＝－f(x)的图象；y＝f(x)的图象――――――――→y＝f(－x)的图象；y＝f(x)的图象――――――――→y＝－f(－x)的图象；y＝ax(a>0，且a≠1)的图象――――――――――→y＝logax(a>0，且a≠1)的图象.(3)伸缩变换y＝f(x)―――――――――――――――――→y＝f(ax).y＝f(x)―――――――――――――――――→y＝Af(x).(4)翻折变换y＝f(x)的图象―――――――――――――――――→y＝|f(x)|的图象；y＝f(x)的图象―――――――――――――――――→y＝f(|x|)的图象.1、【2022年全国甲卷】函数y=(3x−3−x)cosx在区间[−π2,π2]的图象大致为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】A【解析】令f(x)=(3x−3−x)cosx,x∈[−π2,π2]，则f(−x)=(3−x−3x)cos(−x)=−(3x−3−x)cosx=−f(x)，所以f(x)为奇函数，排除BD；又当x∈(0,π2)时，3x−3−x>0,cosx>0，所以f(x)>0，排除C.故选：A.2、【2022年全国乙卷】如图是下列四个函数中的某个函数在区间[−3,3]的大致图象，则该函数是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．y=−x3+3xx2+1B．y=x3−xx2+1C．y=2xcosxx2+1D．y=2sinxx2+1【答案】A【解析】设f(x)=x3−xx2+1，则f(1)=0，故排除B;设ℎ(x)=2xcosxx2+1，当x∈(0,π2)时，0<cosx<1，所以ℎ(x)=2xcosxx2+1<2xx2+1≤1，故排除C;设g(x)=2sinxx2+1，则g(3)=2sin310>0，故排除D.故选：A.3、【2019年新课标2卷理科】设函数的定义域为R，满足，且当时，.若对任意，都有，则m的取值范围是A．B．C．D．【答案】B【解析】时，，，，即右移1个单位，图象变为原来的2倍．如图所示：当时，，令，整理得：，（舍），时，成立，即小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，，故选B．1、如图，函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0，0)，(1，2)，(3，1)，则f的值为()A.1B.2C.D.【答案】B【解析】由可知图f(1)＝2，f(3)＝1，则＝1，f＝f(1)＝2.2、已知函数f(x)＝(x－a)(x－b)(其中a>b)的图象如图所示，则函数g(x)＝ax＋b的图象是()【答案】C【解析】由函数f(x)的象知图a>1，－1<b<0.∴g(x)＝ax＋b在R上是增函，且数g(0)＝1＋b>0.因此选项C足要求满.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3、设函数f(x)＝则满足f(x＋1)<f(2x)的x的取值范围是()A.(－∞，1)B.(0，＋∞)C.(－1，0)D.(－∞，0)【答案】D【解析】作出函数f(x)的象如，所以函图图数f(x)在区间(－∞，0)上函，且为减数当x≥0，时f(x)＝1.因为f(x＋1)<f(2x)，察象可得观图解得x<0，所以足满f(x＋1)<f(2x)的x的取范是值围(－∞，0).4、(多选)(2022·包高中高三考场级学开学试)关于函数f(x)＝|ln|2－x||，下列说法中正确的有()A.f(x)在区间(1，2)上单调递增B.f(x)的图象关于直线x＝2对称C.若x1≠x2，f(x1)＝f(x2)，则x1＋x2＝4D.f(x)有且仅有两个零点【答案】ABD【解析】根据象作出函图变换数f(x)的象，由象知图图f(x)在区间(1，2)上增，故单调递A正确；函数图象于直关线x＝2，故对称B正确；如，若图f(x1)＝f(x2)＝k，直则线y＝k函与数f(x)的象有图4交点，个设最左交点坐分是边两个横标别x1，x2，则x1＋x2＝4不成立，故C；错误f(x)的象图与x有公共点，轴仅两个即函有零点，故数仅两个D正确．故选ABD.考向一作函数的图象【例1】作出下列函数的图象：(1)y＝；(2)y＝|log2(x＋1)|；(3)y＝；(4)y＝x2－2|x|－1.【解析】(1)先作出y＝的图象，保留y＝图象中x≥0的部分，再作出y＝的图象中x>0部分关于y轴的对称部分，即得y＝的图象，如图①实线...