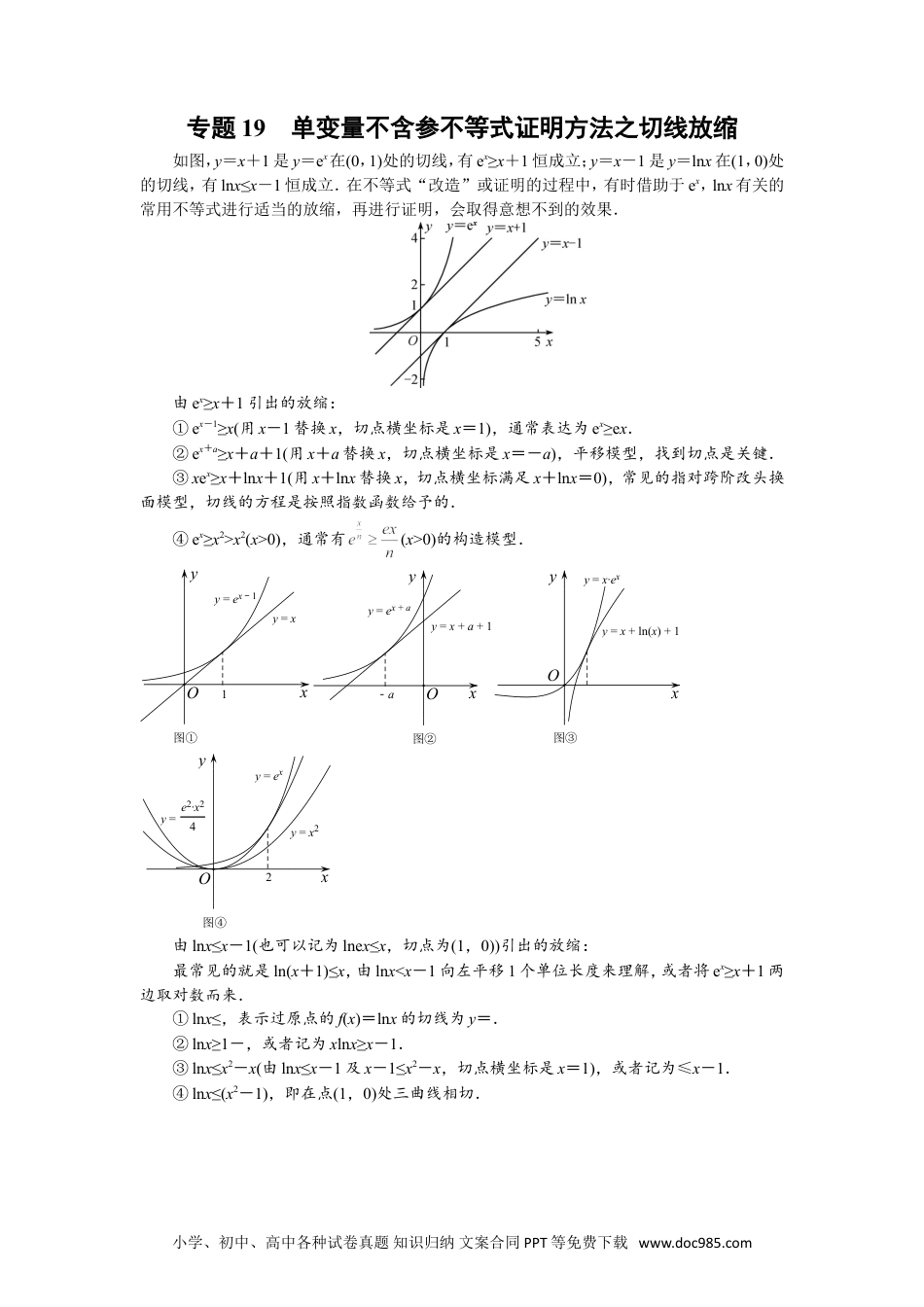
专题19单变量不含参不等式证明方法之切线放缩如图，y＝x＋1是y＝ex在(0，1)处的切线，有ex≥x＋1恒成立；y＝x－1是y＝lnx在(1，0)处的切线，有lnx≤x－1恒成立．在不等式“改造”或证明的过程中，有时借助于ex，lnx有关的常用不等式进行适当的放缩，再进行证明，会取得意想不到的效果．由ex≥x＋1引出的放缩：①ex－1≥x(用x－1替换x，切点横坐标是x＝1)，通常表达为ex≥ex．②ex＋a≥x＋a＋1(用x＋a替换x，切点横坐标是x＝－a)，平移模型，找到切点是关键．③xex≥x＋lnx＋1(用x＋lnx替换x，切点横坐标满足x＋lnx＝0)，常见的指对跨阶改头换面模型，切线的方程是按照指数函数给予的．④ex≥x2>x2(x>0)，通常有(x>0)的构造模型．xy1图①y=xy=ex1Oxy－a图②y=x+a+1y=ex+aOxy图③y=x+lnx()+1y=x∙exOxy2y=x2图④y=e2∙x24y=exO由lnx≤x－1(也可以记为lnex≤x，切点为(1，0))引出的放缩：最常见的就是ln(x＋1)≤x，由lnx<x－1向左平移1个单位长度来理解，或者将ex≥x＋1两边取对数而来．①lnx≤，表示过原点的f(x)＝lnx的切线为y＝．②lnx≥1－，或者记为xlnx≥x－1．③lnx≤x2－x(由lnx≤x－1及x－1≤x2－x，切点横坐标是x＝1)，或者记为≤x－1．④lnx≤(x2－1)，即在点(1，0)处三曲线相切．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comxyy=xee图①y=lnx()Oxyy=11x1图②y=lnx()Oxyy=x2x1图③y=lnx()Oxyy=x1y=12∙x21()1图④y=lnx()O【例题选讲】[例1]求证：当x>0时，不等式2－lnx＋>0恒成立．[例2]已知函数为自然对数的底数）．(1)求函数的最小值；(2)若，证明：．[例3]已知函数f(x)＝lnx－x＋1．(1)讨论f(x)的单调性；(2)求证：当x∈(1，＋∞)时，1<<x；[例4]已知函数，其中．(1)讨论的单调性；(2)当时，证明：；(3)求证：对任意的且，都有：．(其中为自然对数的底数)．【对点精练】1．已知函数f(x)＝lnx－a2x2＋ax．(1)试讨论f(x)的单调性；(2)若a＝1，求证：当x>0时，f(x)<e2x－x2－2．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．已知函数．(1)设是函数的极值点，求的值并讨论的单调性；(2)当时，证明：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3．若函数f(x)＝ex－ax－1(a＞0)在x＝0处取极值．(1)求a的值，并判断该极值是函数的最大值还是最小值；(2)证明：1＋＋＋…＋＞ln(n＋1)(n∈N*)．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4．(2018·全国Ⅰ改编)已知函数f(x)＝aex－lnx－1．(1)设x＝2是f(x)的极值点，求a的值并求f(x)的单调区间；(2)求证：当a＝时，f(x)≥0．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．已知函数f(x)＝x－1－alnx．(1)若f(x)≥0，求a的值；(2)设m为整数，且对于任意正整数n，·…·＜m，求m的最小值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6．已知函数f(x)＝ln(1＋x)．(1)求证：当x∈(0，＋∞)时，<f(x)<x；(2)已知e为自然对数的底数，求证：∀n∈N*，<·…·<e．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com