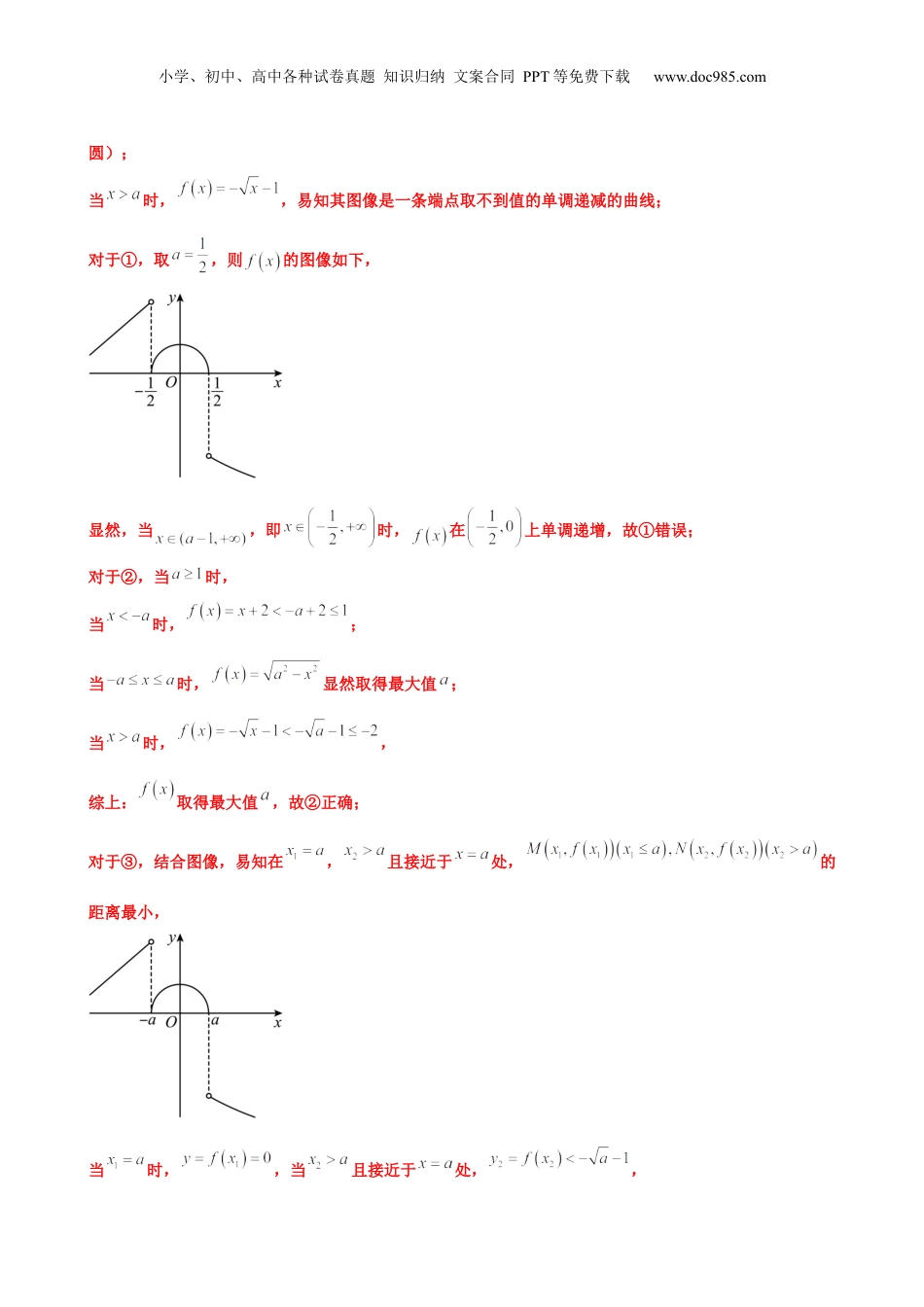
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com押北京卷15题分段函数与函数的零点核心考点考情统计考向预测备考策略分段函数的性质2023·北京卷T15可以预测2024年新高考命题方向将继续分段函数的综合问题或函数的零点作为压轴题展开命题．分段函数的综合问题或函数的零点中填空题较难，纵观近几年的新高考试题，分别考查分段函数的性质、函数的零点，同时备考也需强化函数的性质和数形结合的应用，也是高考冲刺复习的重点复习内容。分段函数开放题2022·北京卷T14函数零点2021·北京卷T151．（2023·北京卷T15）设，函数，给出下列四个结论：①在区间上单调递减；②当时，存在最大值；③设，则；④设．若存在最小值，则a的取值范围是．其中所有正确结论的序号是．【答案】②③【解析】依题意，，当时，，易知其图像为一条端点取不到值的单调递增的射线；当时，，易知其图像是，圆心为，半径为的圆在轴上方的图像（即半小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com圆）；当时，，易知其图像是一条端点取不到值的单调递减的曲线；对于①，取，则的图像如下，显然，当，即时，在上单调递增，故①错误；对于②，当时，当时，；当时，显然取得最大值；当时，，综上：取得最大值，故②正确；对于③，结合图像，易知在，且接近于处，的距离最小，当时，，当且接近于处，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com此时，，故③正确；对于④，取，则的图像如下，因为，结合图像可知，要使取得最小值，则点在上，点在，同时的最小值为点到的距离减去半圆的半径，此时，因为的斜率为，则，故直线的方程为，联立，解得，则，显然在上，满足取得最小值，即也满足存在最小值，故的取值范围不仅仅是，故④错误.2．（2022·北京卷T14）设函数若存在最小值，则a的一个取值为；a的最大值为．【答案】0（答案不唯一）1小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】若时，，∴；若时，当时，单调递增，当时，，故没有最小值，不符合题目要求；若时，当时，单调递减，，当时，∴或，解得，综上可得；3．（2021·北京卷T15）已知函数，给出下列四个结论：①若，恰有2个零点；②存在负数，使得恰有1个零点；③存在负数，使得恰有3个零点；④存在正数，使得恰有3个零点．其中所有正确结论的序号是．【答案】①②④【解析】对于①，当时，由，可得或，①正确；对于②，考查直线与曲线相切于点，对函数求导得，由题意可得，解得，所以，存在，使得只有一个零点，②正确；对于③，当直线过点时，，解得，所以，当时，直线与曲线有两个交点，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com若函数有三个零点，则直线与曲线有两个交点，直线与曲线有一个交点，所以，，此不等式无解，因此，不存在，使得函数有三个零点，③错误；对于④，考查直线与曲线相切于点，对函数求导得，由题意可得，解得，所以，当时，函数有三个零点，④正确.1.分段函数(1)若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数.分段函数表示的是一个函数.(2)分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集.2.根据分段函数解析式求函数值，首先确定自变量的值属于哪个区间，其次选定相应的解析式代入求解.3.已知函数值或函数的取值范围求自变量的值或范围时，应根据每一段的解析式分别求解，但要注意检验所求自变量的值或范围是否符合相应段的自变量的取值范围.4.判断函数零点个数的方法：(1)利用零点存在定理判断.(2)代数法：求方程f(x)＝0的实数根.(3)几何法：对于不易求根的方程，将它与函数y＝f(x)的图象联系起来，利用函数的性质找出零点或利用两个函数图象的交点求解.在利用函数性质时，可用求导的方法判断函数的单调性.5.利用函数零点的情况求参数值(或取值范围)的三种方法小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．已知函数，若存在最小值，则的最大...