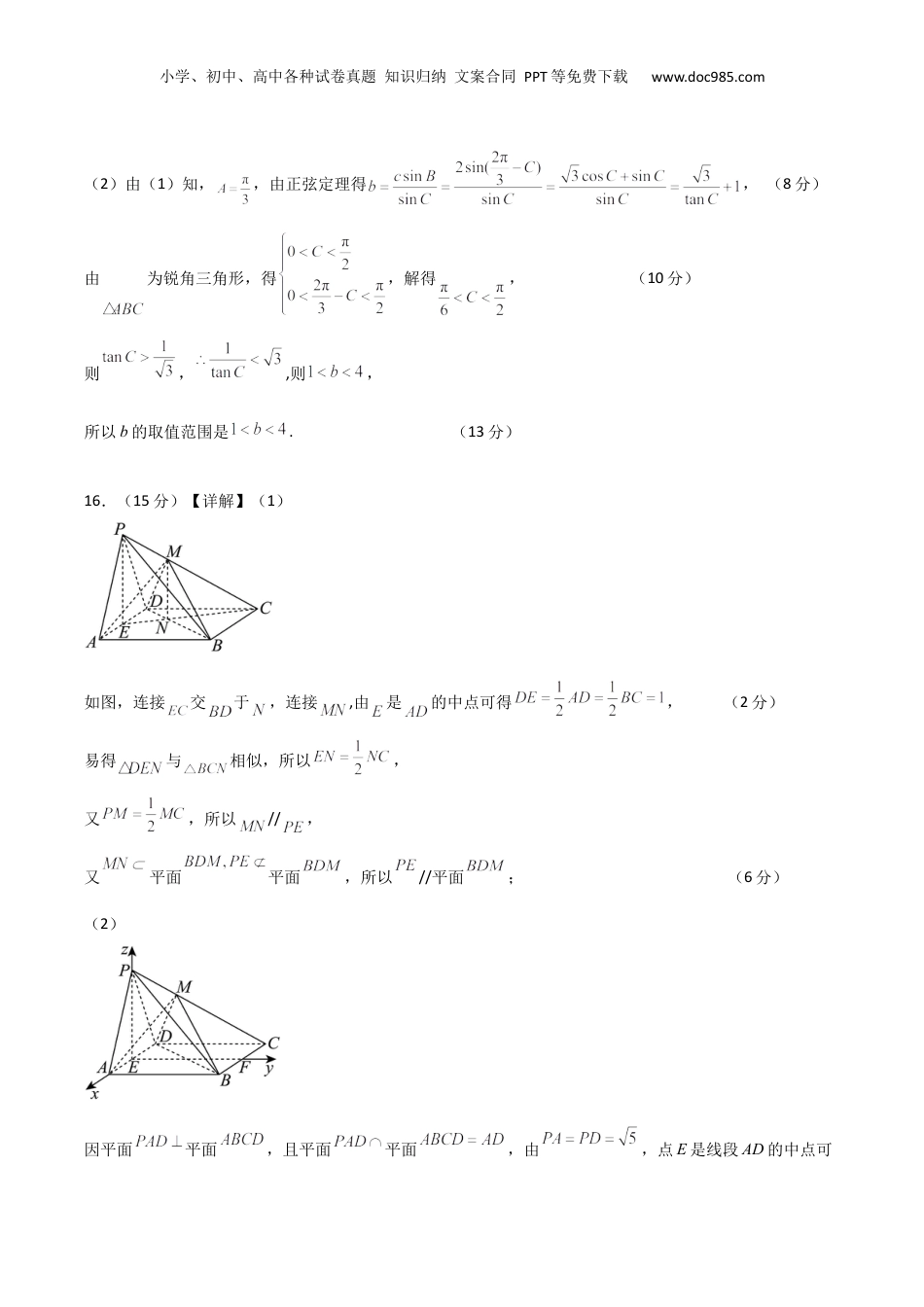
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2024年高考数学临考押题卷02（新高考通用）数学（考试时间：120分钟试卷满分：150分）一、单选题（本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的）12345678BBABDDCA二、多选题（本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对得6分，部分选对得部分分，有选错得0分）91011ACDBCABD三、填空题（本题共3小题，每小题5分，共15分）12．.13．14．四、解答题（本题共5小题，共77分，其中15题13分，16题15分，17题15分，18题17分，19题17分，解答应写出文字说明、证明过程或演算步骤）15．（13分）【详解】（1）在中，由及正弦定理，得，（2分）则，（4分）即，而，于是，又，所以.（6分）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）由（1）知，，由正弦定理得，（8分）由为锐角三角形，得，解得，（10分）则，,则，所以b的取值范围是.（13分）16．（15分）【详解】（1）如图，连接交于，连接,由是的中点可得，（2分）易得与相似，所以，又，所以//，又平面平面，所以//平面；（6分）（2）因平面平面，且平面平面，由，点E是线段AD的中点可小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com得又平面，故得平面.如图，取的中点为,分别以为轴的正方向，建立空间直角坐标系.则，，，则，.（8分）设平面的法向量为，由，则，故可取；（10分）设平面的法向量为，由，则，故可取.（12分）故平面与平面的夹角余弦值为，（13分）所以平面与平面的夹角为.（15分）17．（15分）【详解】（1）记电压“不超过200V”、“在200V~240V之间”、“超过240V”分别为事件A，B，C，“该机器生产的零件为不合格品”为事件D．因为，所以，，．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，所以该机器生产的零件为不合格品的概率为0.09．（7分）（2）从该机器生产的零件中随机抽取n件，设不合格品件数为X，则，所以．（9分）由，解得．（13分）所以当时，；当时，；所以最大．因此当时，最大．（15分）18．（17分）【详解】（1）（i）根据已知条件，有，解得，又在椭圆上，将的坐标代入椭圆方程有：，解得，所以椭圆的方程为：.（4分）（ii）因为抛物线的焦点与椭圆的右焦点重合，所以抛物线方程为；直线与椭圆联立，整理有：，由韦达定理得：，，（5分）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com；直线与抛物线联立，整理得，由韦达定理得：，，（6分）；，若与方向相同，则，若与方向相反，则，故.（8分）（2）椭圆的短轴长为2，所以椭圆方程为：，因为，，三点共线，所以，解得；同理：，，三点共线，所以，解得；（10分）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com设，此时，，因为，所以，所以；（11分）又设，，所以，因为，令，，此时，所以，其中，，因为，所以为开口向下，对称轴为，其中，故当时，取得最大值，最大值为：，所以有最小值为，令，解得或，因为，所以（舍去），所以，解得，此时，，又，所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以点坐标为.（15分）19．（17分）【详解】（1）因为，所以，，．设，，则，所以在上单调递增，所以，因此．（4分）（2）函数，，方法一：，当时，注意到，故，因此，由（1）得，因此，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以在上单调递增，从而，满足题意；当时，令，，因为，所以存在，使得，则当时，，，所以在上单调递减，从而，所以在上单调递减，因此，不合题意；综上，．（10分）方法二：，当时，注意到，故，因此，由（1）得，因此，所以在上单调递增，从而，满足题意；当时，先证明当时，.令，则，令，则，所以在上单调递减，有，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以在上单调递减，有，因此当时，...