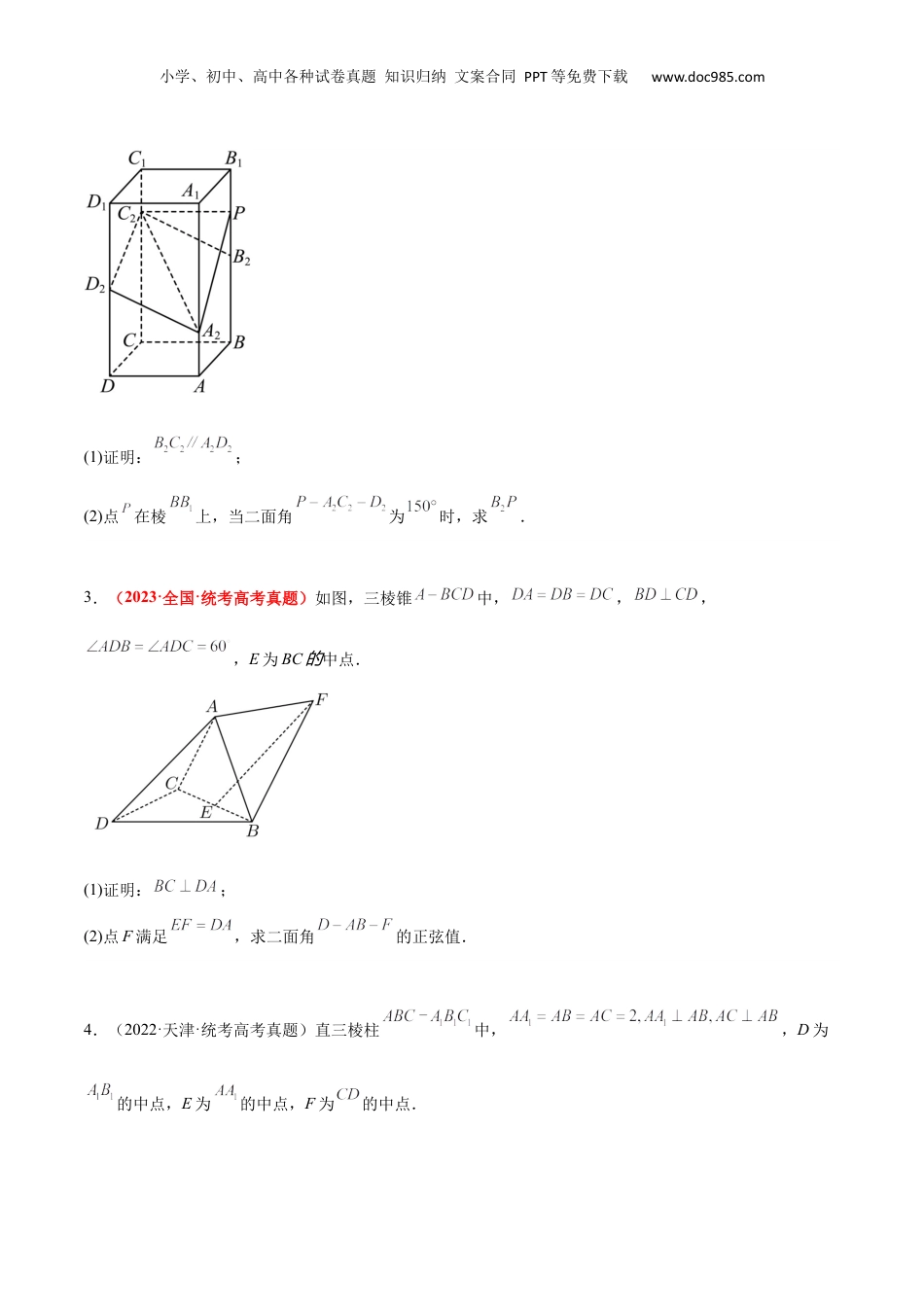
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第36练空间向量及其应用（精练）一、解答题1．（2023·北京·统考高考真题）如图，在三棱锥中，平面，．(1)求证：平面PAB；(2)求二面角的大小．2．（2023·全国·统考高考真题）如图，在正四棱柱中，．点分别在棱,上，．刷真题明导向小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：；(2)点在棱上，当二面角为时，求．3．（2023·全国·统考高考真题）如图，三棱锥中，，，，E为BC的中点．(1)证明：；(2)点F满足，求二面角的正弦值．4．（2022·天津·统考高考真题）直三棱柱中，，D为的中点，E为的中点，F为的中点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求证：平面；(2)求直线与平面所成角的正弦值；(3)求平面与平面夹角的余弦值．5．（2022·浙江·统考高考真题）如图，已知和都是直角梯形，，，，，，，二面角的平面角为．设M，N分别为的中点．(1)证明：；(2)求直线与平面所成角的正弦值．6．（2022·全国·统考高考真题）如图，是三棱锥的高，，，E是的中点．(1)证明：平面；(2)若，，，求二面角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7．（2022·全国·统考高考真题）在四棱锥中，底面．(1)证明：；(2)求PD与平面所成的角的正弦值．8．（2022·全国·统考高考真题）如图，四面体中，，E为的中点．(1)证明：平面平面；(2)设，点F在上，当的面积最小时，求与平面所成的角的正弦值．9．（2022·北京·统考高考真题）如图，在三棱柱中，侧面为正方形，平面平面，，M，N分别为，AC的中点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)求证：平面；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB与平面BMN所成角的正弦值．条件①：；条件②：．注：如果选择条件①和条件②分别解答，按第一个解答计分．10．（2022·全国·统考高考真题）如图，直三棱柱的体积为4，的面积为．(1)求A到平面的距离；(2)设D为的中点，，平面平面，求二面角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【A组在基础中考查功底】一、解答题1．（2023·新疆和田·校考一模）如图，在三棱柱中，平面为线段的中点．(1)求证：；(2)求直线与平面所成角大小．2．（2023秋·江苏南京·高三校联考阶段练习）已知四棱锥P-ABCD中，PD⊥平面ABCD，，，AB⊥DA，AB∥CD．(1)求证：平面PAD⊥平面PCD；(2)设M是棱PC上的点，若二面角M-BD-A的余弦值为，试求直线BC与平面BDM所成角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3．（2023·全国·高三专题练习）如图，在棱长为1的正方体中，E为线段的中点，F为线段的中点．（1）求点到直线的距离；（2）求点到平面的距离；4．（2023春·北京海淀·高三北京交通大学附属中学校考阶段练习）如图，在三棱柱中，侧面为正方形，平面平面，，M，N分别为，AC的中点．(1)求证：平面；(2)若，求直线AB与平面BMN所成角的正弦值．5．（2023·全国·高三专题练习）如图，已知长方体＝＝1，直线BD与平面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所成的角为30°，AE垂直BD于E，F为的中点．(1)求异面直线AE与BF所成的角的余弦；(2)求点A到平面BDF的距离．6．（2023·全国·模拟预测）在图1中，四边形为梯形，，，，，过点A作，交于．现沿将折起，使得，得到如图2所示的四棱锥，在图2中解答下列两问：(1)求四棱锥的体积；(2)若F在侧棱上，，求证：二面角为直二面角．7．（2023·全国·高三专题练习）在斜三棱柱中，是等腰直角三角形，，平面底面，.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：；(2)求二面角的正弦值.8．（2023·陕西西安·校考模拟预测）如图所示，四棱锥的底面是矩形，底面，，，，．(1)证...