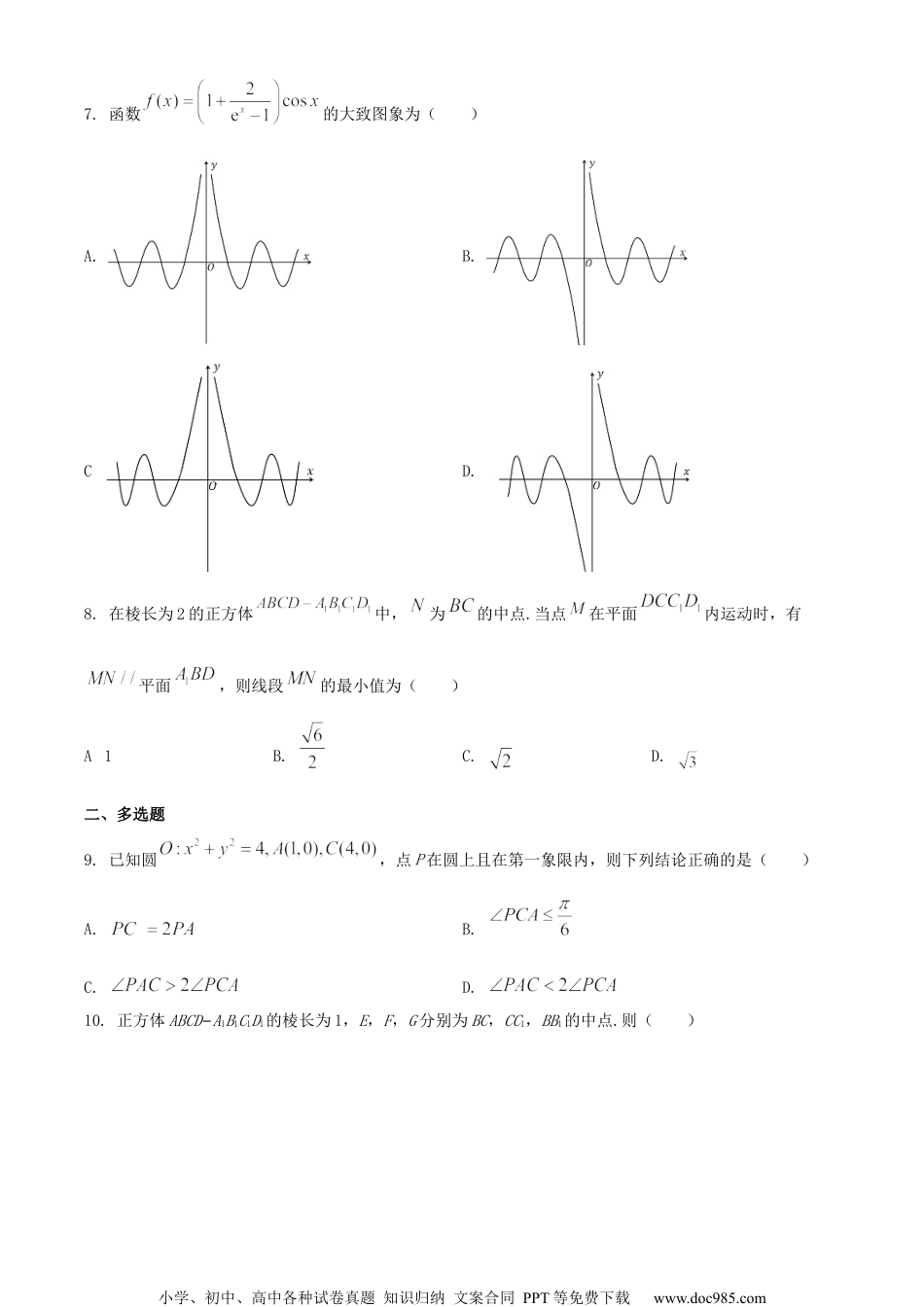
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com滨海中学2022届高考指导卷（一）数学试题分值：150时间：120命题：周华俊审核：季东升一、单选题1.从集合的非空子集中随机选择两个不同的集合A，B，则的概率为（）A.B.C.D.2.复数满足，则（）A.B.C.D.3.设，则有（）A.B.C.D.4.已知正项数列满足，当最大时，的值为（）A.2B.3C.4D.55.假设，是两个事件，且，，则下列结论一定成立的是（）A.B.C.D.6.若，（）A.B.C.D.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7.函数的大致图象为（）A.B.C.D.8.在棱长为2的正方体中，为的中点.当点在平面内运动时，有平面，则线段的最小值为（）A.1B.C.D.二、多选题9.已知圆，点P在圆上且在第一象限内，则下列结论正确的是（）A.B.C.D.10.正方体ABCD−A1B1C1D1的棱长为1，E，F，G分别为BC，CC1，BB1的中点.则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体所得的截面面积为D.点C与点G到平面AEF的距离相等11.十七世纪至十八世纪的德国数学家莱布尼兹是世界上第一个提出二进制记数法的人，用二进制记数只需数字0和1，对于整数可理解为逢二进，例如：自然数1在二进制中就表示为1，2表示为10，3表示为11，7表示为111，即，，其中，或，记为上述表示中0的个数，如，．则下列说法中正确的是（）．A.B.C.D.1到127这些自然数的二进制表示中的自然数有35个12.已知抛物线：，圆：，过点的直线与圆交于，两点，交抛物线于，两点，则满足的直线有三条的的值有（）A.1B.2C.3D.4三、填空题13.某办公楼前有7个连成一排的车位，现有三辆不同型号的车辆停放，恰有两辆车停放在相邻车位的概率是__________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com14.若函数在上是减函数，则实数的取值范围为___________.15.计算机(computer)是20世纪最先进的科学技术发明之一，对人类的生产活动和社会活动产生了极其重要的影响．计算机处理数据时，使用的是二进制．二进制数是用0和1表示的数，它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”．二进制数对应的十进制数记为，即，其中．那么满足中有且只有4个0的所有二进制数对应的十进制数的和为_________．16.已知数列各项都是正数，且，若是递增数列，则的取值范围是_______.若，，且，则整数_______.四、解答题17.已知函数．（1）讨论函数的单调性；（2）当时，求函数在上的零点个数．18.如图，已知抛物线，椭圆：中心在原点，焦点在y轴上，且离心率为．直线交于A、B两点，交于M、N两点．是上的点，且始终位于直线l的右上方．连接、，的平分线交y轴于H，交的左侧部分于T．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）求证：轴；（2）若M是的中点，是否存在最大值？若存在，求出使取得最大值时m的值；若不存在，请说明理由．19.在中，，和的平分线交于点.（1）若，求的值；（2）若，求的大小.20.已知，试求的最大值．21.如图，在四棱锥中，，，∥，，，.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）证明：平面ABCD.（2）若M为PD的中点，求P到平面的距离.22.冰壶是2022年2月4日至2月20日在中国举行的第24届冬季奥运会的比赛项目之一．冰壶比赛的场地如图所示，其中左端（投掷线MN的左侧）有一个发球区，运动员在发球区边沿的投掷线MN将冰壶掷出，使冰壶沿冰道滑行，冰道的右端有一圆形的营垒，以场上冰壶最终静止时距离营垒区圆心O的远近决定胜负，甲、乙两人进行投掷冰壶比赛，规定冰壶的重心落在圆O中，得3分，冰壶的重心落在圆环A中，得2分，冰壶的重心落在圆环B中，得1分，其余情况均得0分．已知甲、乙投掷冰壶的结果互不影响，甲、乙得3分的概率分别为，；甲、乙得2分的概率分别为，；甲、乙得1分的概率分别为，．（1）求甲、乙两人所得分数相同的概率；（2）设甲、乙两人所得的分数之和为X，求X的分布列和期望．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com