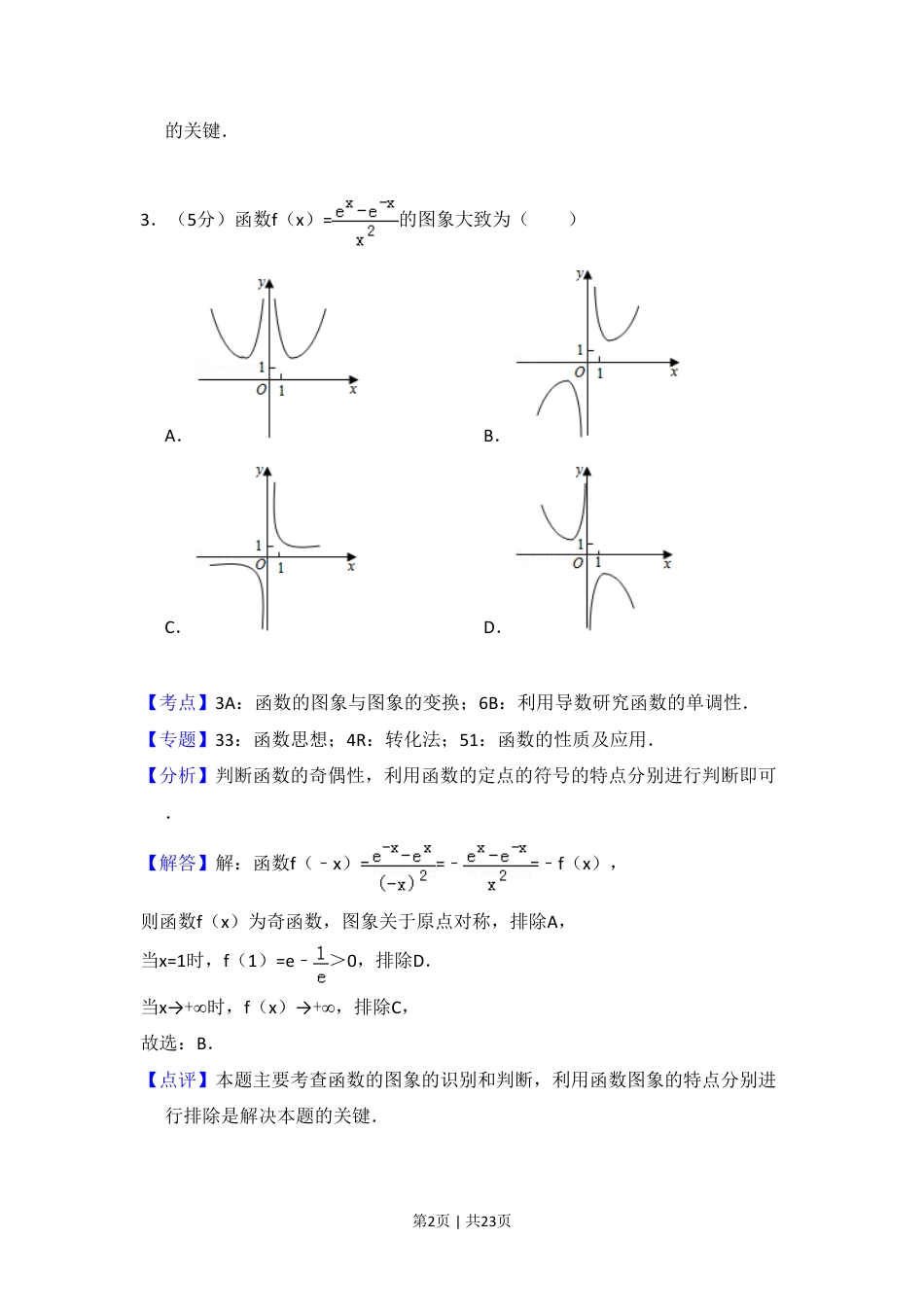
第1页|共23页2018年全国统一高考数学试卷(理科)(新课标Ⅱ)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.(5分)=()A.iB.C.D.【考点】A5:复数的运算.菁优网版权所有【专题】11:计算题;35:转化思想;49:综合法;5N:数系的扩充和复数.【分析】利用复数的除法的运算法则化简求解即可.【解答】解:==+.故选:D.【点评】本题考查复数的代数形式的乘除运算,是基本知识的考查.2.(5分)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为()A.9B.8C.5D.4【考点】1A:集合中元素个数的最值.菁优网版权所有【专题】32:分类讨论;4O:定义法;5J:集合.【分析】分别令x=﹣1,0,1,进行求解即可.【解答】解:当x=﹣1时,y2≤2,得y=﹣1,0,1,当x=0时,y2≤3,得y=﹣1,0,1,当x=1时,y2≤2,得y=﹣1,0,1,即集合A中元素有9个,故选:A.【点评】本题主要考查集合元素个数的判断,利用分类讨论的思想是解决本题第2页|共23页的关键.3.(5分)函数f(x)=的图象大致为()A.B.C.D.【考点】3A:函数的图象与图象的变换;6B:利用导数研究函数的单调性.菁优网版权所有【专题】33:函数思想;4R:转化法;51:函数的性质及应用.【分析】判断函数的奇偶性,利用函数的定点的符号的特点分别进行判断即可.【解答】解:函数f(﹣x)==﹣=﹣f(x),则函数f(x)为奇函数,图象关于原点对称,排除A,当x=1时,f(1)=e﹣>0,排除D.当x→+∞时,f(x)→+∞,排除C,故选:B.【点评】本题主要考查函数的图象的识别和判断,利用函数图象的特点分别进行排除是解决本题的关键.第3页|共23页4.(5分)已知向量,满足||=1,=﹣1,则•(2)=()A.4B.3C.2D.0【考点】91:向量的概念与向量的模;9O:平面向量数量积的性质及其运算.菁优网版权所有【专题】11:计算题;38:对应思想;4O:定义法;5A:平面向量及应用.【分析】根据向量的数量积公式计算即可.【解答】解:向量,满足||=1,=﹣1,则•(2)=2﹣=2+1=3,故选:B.【点评】本题考查了向量的数量积公式,属于基础题5.(5分)双曲线=1(a>0,b>0)的离心率为,则其渐近线方程为()A.y=±xB.y=±xC.y=±xD.y=±x【考点】KC:双曲线的性质.菁优网版权所有【专题】35:转化思想;4O:定义法;5D:圆锥曲线的定义、性质与方程.【分析】根据双曲线离心率的定义求出a,c的关系,结合双曲线a,b,c的关系进行求解即可.【解答】解: 双曲线的离心率为e==,则=====,即双曲线的渐近线方程为y=±x=±x,故选:A.【点评】本题主要考查双曲线渐近线的求解,结合双曲线离心率的定义以及渐近线的方程是解决本题的关键.第4页|共23页6.(5分)在△ABC中,cos=,BC=1,AC=5,则AB=()A.4B.C.D.2【考点】HR:余弦定理.菁优网版权所有【专题】11:计算题;35:转化思想;49:综合法;58:解三角形.【分析】利用二倍角公式求出C的余弦函数值,利用余弦定理转化求解即可.【解答】解:在△ABC中,cos=,cosC=2×=﹣,BC=1,AC=5,则AB====4.故选:A.【点评】本题考查余弦定理的应用,考查三角形的解法以及计算能力.7.(5分)为计算S=1﹣+﹣+…+﹣,设计了如图的程序框图,则在空白框中应填入()A.i=i+1B.i=i+2C.i=i+3D.i=i+4【考点】E7:循环结构;EH:绘制程序框图解决问题.菁优网版权所有第5页|共23页【专题】38:对应思想;4B:试验法;5K:算法和程序框图.【分析】模拟程序框图的运行过程知该程序运行后输出的S=N﹣T,由此知空白处应填入的条件.【解答】解:模拟程序框图的运行过程知,该程序运行后输出的是S=N﹣T=(1﹣)+(﹣)+…+(﹣);累加步长是2,则在空白处应填入i=i+2.故选:B.【点评】本题考查了循环程序的应用问题,是基础题.8.(5分)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()A.B.C.D.【考点...