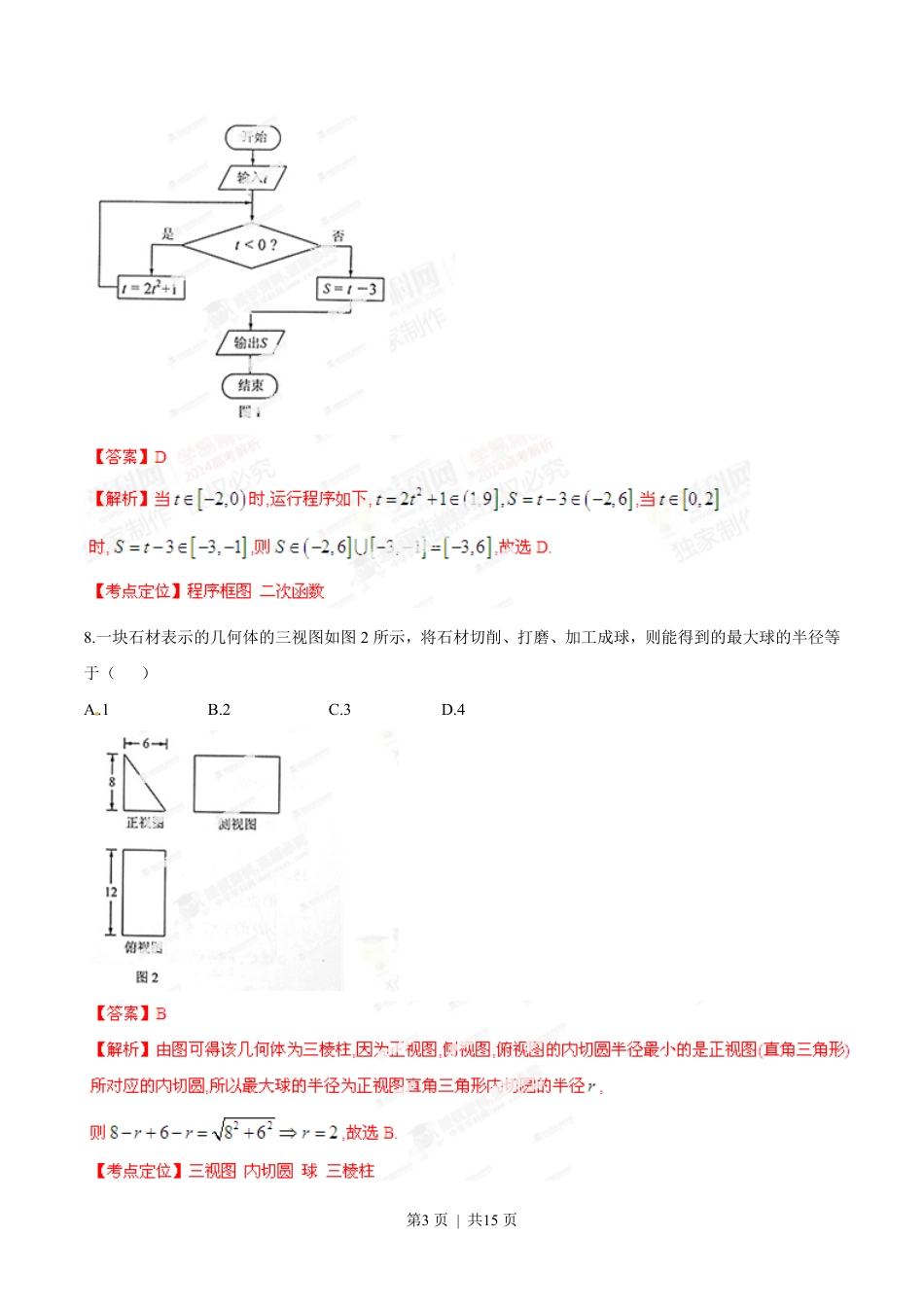
第1页|共15页一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设命题2:,10pxRx"Î+>,则pØ为()200.,10AxRx$Î+>200.,10BxRx$Î+£200.,10CxRx$Î+<2.,10DxRx"Î+£2.已知集合{|2},{|13}AxxBxx=>=<<,则AB=I().{|2}Axx>.{|1}Bxx>.{|23}Cxx<<.{|13}Dxx<<【答案】C[来源:学&科&网]【解析】由交集的定义可得/23ABxx=<<I,故选C.【考点定位】集合交集3.对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为123,,ppp,则()123.Appp=<231.Bppp=<132.Cppp=<123.Dppp==4.下列函数中,既是偶函数又在区间(,0)-¥上单调递增的是()第2页|共15页21.()Afxx=2.()1Bfxx=+3.()Cfxx=.()2xDfx-=5.在区间[2,3]-上随机选取一个数X,则1X£的概率为()4.5A3.5B2.5C1.5D6.若圆221:1Cxy+=与圆222:680Cxyxym+--+=,则m=().21A.19B.9C.11D-7.执行如图1所示的程序框图,如果输入的2,2tÎ-,则输出的S属于()A.6,2--B.5,1--C.4,5-D.3,6-第3页|共15页8.一块石材表示的几何体的三视图如图2所示,将石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4第4页|共15页9.若1201xx<<<,则()A.2121lnlnxxeexx->-B.2121lnlnxxeexx-<-C.1221xxxexe>D.1221xxxexe<10.在平面直角坐标系中,O为原点,1,0A-,03B,,30C,,动点D满足1CD=,[来源:学_科_网Z_X_X_K]则OAOBOD++的取值范围是()A.46,B.19-119+1,C.2327,D.7-17+1,[来源:学|科|网Z|X|X|K]二.填空题:本大题共5小题,每小题5分,共25分.第5页|共15页11.复数23ii+(i为虚数单位)的实部等于_________.12.在平面直角坐标系中,曲线222:212xtCyt=+=+(t为参数)的普通方程为___________.[来源:学科网]13.若变量yx,满足约束条件£+£14yyxxy,则yxz+=2的最大值为_________.第6页|共15页14.平面上以机器人在行进中始终保持与点01,F的距离和到直线1-=x的距离相等.若机器人接触不到过点01,-P且斜率为k的直线,则k的取值范围是___________.15.若axexfx++=1ln3是偶函数,则=a____________.第7页|共15页三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算过程.16.(本小题满分12分)已知数列na的前n项和Î+=NnnnSn,22.(1)求数列na的通项公式;(2)设nnanabn12-+=,求数列nb的前n2项和.【答案】(1)nan=(2)21222nnTn+=+-【解析】试题分析:(1)题目已知,nnaS之间的关系,令1n=,利用11aS=,即可求的1a的值,令2n,利用na与前n项和之间的关系1nnnaSS-=-即可得到na,令1n=检验首项即可得到na的通项公式.第8页|共15页17.(本小题满分12分)某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:ababababababababababababababab,,,,,,,,,,,,,,,,,,,,,,,,,,,,,其中aa,分别表示甲组研发成功和失败;bb,分别表示乙组研发成功和失败.(1)若某组成功研发一种新产品,则给改组记1分,否记0分,试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;(2)若该企业安排甲、乙两组各自研发一种新产品,试估算恰有一组研发成功的概率.【答案】(1)23x=甲,229s=甲,35x=乙,2625s=乙,甲组优于乙组(2)715PE=第9页|共15页18.(本小题满分12分)如图3,已知二面角MN--的大小为60,菱形ABCD在面内,,AB两点在棱MN上,60BAD=,E是AB的中点,DO面,垂足为O.(1)证明:AB平面ODE;(2)求异面直线BC与OD所成角的余弦值.[来源:学科网]第10页|共15页第11页|共15页19.(本小题满分13分)如图4,在平面四边形ABCD中,32,2,7,1,====ADCEAECDEABDA,3=BEC(1)求CEDsin的值;(2)求BE的长(2)由题设可得203<<,于...