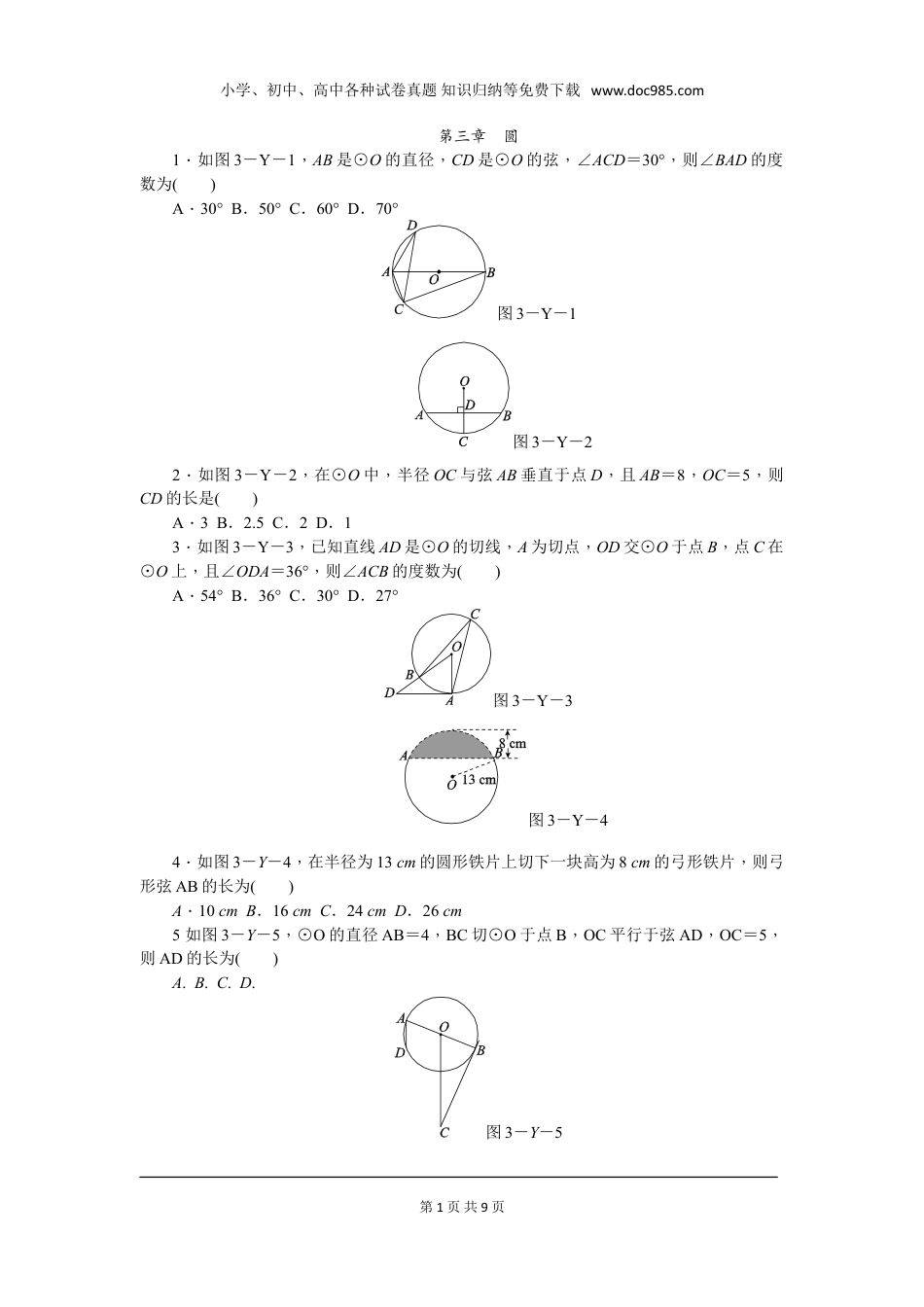
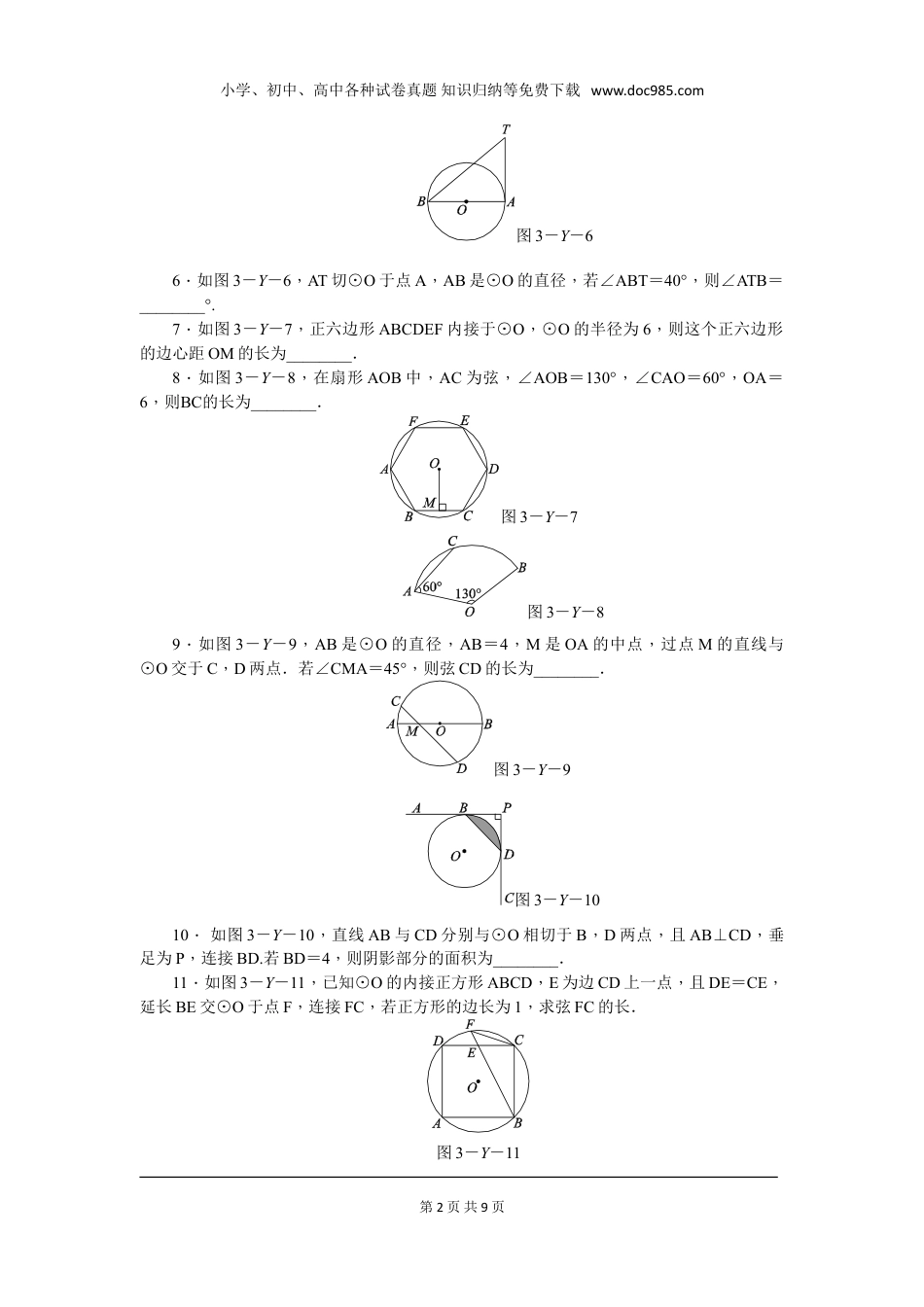
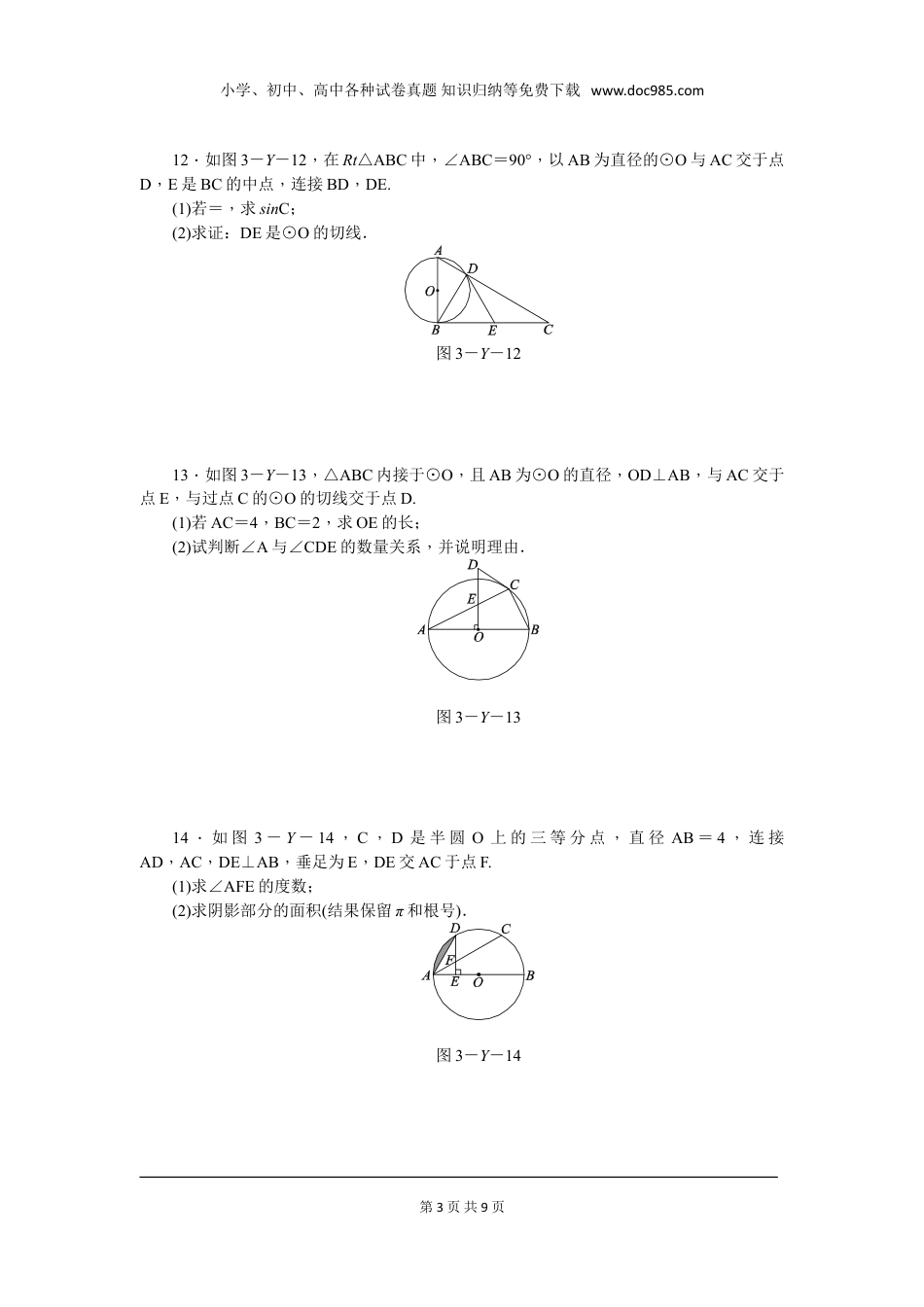
小学、初中、高中各种试卷真题知识归纳等免费下载www.doc985.com第三章圆1．如图3－Y－1，AB是⊙O的直径，CD是⊙O的弦，∠ACD＝30°，则∠BAD的度数为()A．30°B．50°C．60°D．70°图3－Y－1图3－Y－22．如图3－Y－2，在⊙O中，半径OC与弦AB垂直于点D，且AB＝8，OC＝5，则CD的长是()A．3B．2.5C．2D．13．如图3－Y－3，已知直线AD是⊙O的切线，A为切点，OD交⊙O于点B，点C在⊙O上，且∠ODA＝36°，则∠ACB的度数为()A．54°B．36°C．30°D．27°图3－Y－3图3－Y－44．如图3－Y－4，在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片，则弓形弦AB的长为()A．10cmB．16cmC．24cmD．26cm5如图3－Y－5，⊙O的直径AB＝4，BC切⊙O于点B，OC平行于弦AD，OC＝5，则AD的长为()A.B.C.D.图3－Y－5第1页共9页小学、初中、高中各种试卷真题知识归纳等免费下载www.doc985.com图3－Y－66．如图3－Y－6，AT切⊙O于点A，AB是⊙O的直径，若∠ABT＝40°，则∠ATB＝________°.7．如图3－Y－7，正六边形ABCDEF内接于⊙O，⊙O的半径为6，则这个正六边形的边心距OM的长为________．8．如图3－Y－8，在扇形AOB中，AC为弦，∠AOB＝130°，∠CAO＝60°，OA＝6，则BC的长为________．图3－Y－7图3－Y－89．如图3－Y－9，AB是⊙O的直径，AB＝4，M是OA的中点，过点M的直线与⊙O交于C，D两点．若∠CMA＝45°，则弦CD的长为________．图3－Y－9图3－Y－1010．如图3－Y－10，直线AB与CD分别与⊙O相切于B，D两点，且AB⊥CD，垂足为P，连接BD.若BD＝4，则阴影部分的面积为________．11．如图3－Y－11，已知⊙O的内接正方形ABCD，E为边CD上一点，且DE＝CE，延长BE交⊙O于点F，连接FC，若正方形的边长为1，求弦FC的长．图3－Y－11第2页共9页小学、初中、高中各种试卷真题知识归纳等免费下载www.doc985.com12．如图3－Y－12，在Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O与AC交于点D，E是BC的中点，连接BD，DE.(1)若＝，求sinC；(2)求证：DE是⊙O的切线．图3－Y－1213．如图3－Y－13，△ABC内接于⊙O，且AB为⊙O的直径，OD⊥AB，与AC交于点E，与过点C的⊙O的切线交于点D.(1)若AC＝4，BC＝2，求OE的长；(2)试判断∠A与∠CDE的数量关系，并说明理由．图3－Y－1314．如图3－Y－14，C，D是半圆O上的三等分点，直径AB＝4，连接AD，AC，DE⊥AB，垂足为E，DE交AC于点F.(1)求∠AFE的度数；(2)求阴影部分的面积(结果保留π和根号)．图3－Y－14第3页共9页小学、初中、高中各种试卷真题知识归纳等免费下载www.doc985.com15．如图3－Y－15，PA，PB是⊙O的切线，A，B为切点，∠APB＝60°，连接PO并延长与⊙O交于点C，连接AC，BC.(1)求证：四边形ACBP是菱形；(2)若⊙O的半径为1，求菱形ACBP的面积．图3－Y－15第4页共9页小学、初中、高中各种试卷真题知识归纳等免费下载www.doc985.com1．C[解析]如图，连接BD， ∠ACD＝30°，∴∠ABD＝30°. AB为⊙O的直径，∴∠ADB＝90°，∴∠BAD＝90°－∠ABD＝60°.故选C.2．C[解析]如图，连接OA，设CD＝x， OA＝OC＝5，∴OD＝5－x. OC⊥AB，∴由垂径定理，得AD＝4，由勾股定理，得52＝42＋(5－x)2，∴x＝2，∴CD＝2.故选C.3．D[解析] AD为⊙O的切线，∴AD⊥OA，即∠OAD＝90°. ∠ODA＝36°，∴∠AOD＝54°，∴∠ACB＝∠AOD＝27°.故选D.4．C[解析]过点O作OC⊥AB于点D，交⊙O于点C. OB＝13cm，CD＝8cm，∴OD＝5cm.在Rt△BOD中，BD＝＝12cm，∴AB＝2BD＝24cm.5．B[解析]如图，连接BD. AB是⊙O的直径，∴∠ADB＝90°. OC∥AD，∴∠A＝∠BOC，∴cosA＝cos∠BOC. BC切⊙O于点B，∴OB⊥BC，∴cos∠BOC＝＝，∴cosA＝.第5页共9页小学、初中、高中各种试卷真题知识归纳等免费下载www.doc985.com又 cosA＝，AB＝4，∴AD＝.故选B.6．507．3[解析]如图，连接OB， 六边形ABCDEF是⊙O的内接正六边形，∴∠BOM＝＝30°，∴OM＝OB·cos∠BOM＝6×＝3.故答案为：3.8.π[解析]连接OC，如图， OA＝OC，∴∠OCA＝∠CAO＝60°，∴∠AOC＝60°，∴∠BOC＝130°－60°＝70°，∴BC的长为＝π.故答案为：π.9.[解析]连接OD，过点O作OE⊥CD于点E，如图所示．则CE＝DE. AB是⊙O的直径，AB＝4，M是OA的中...