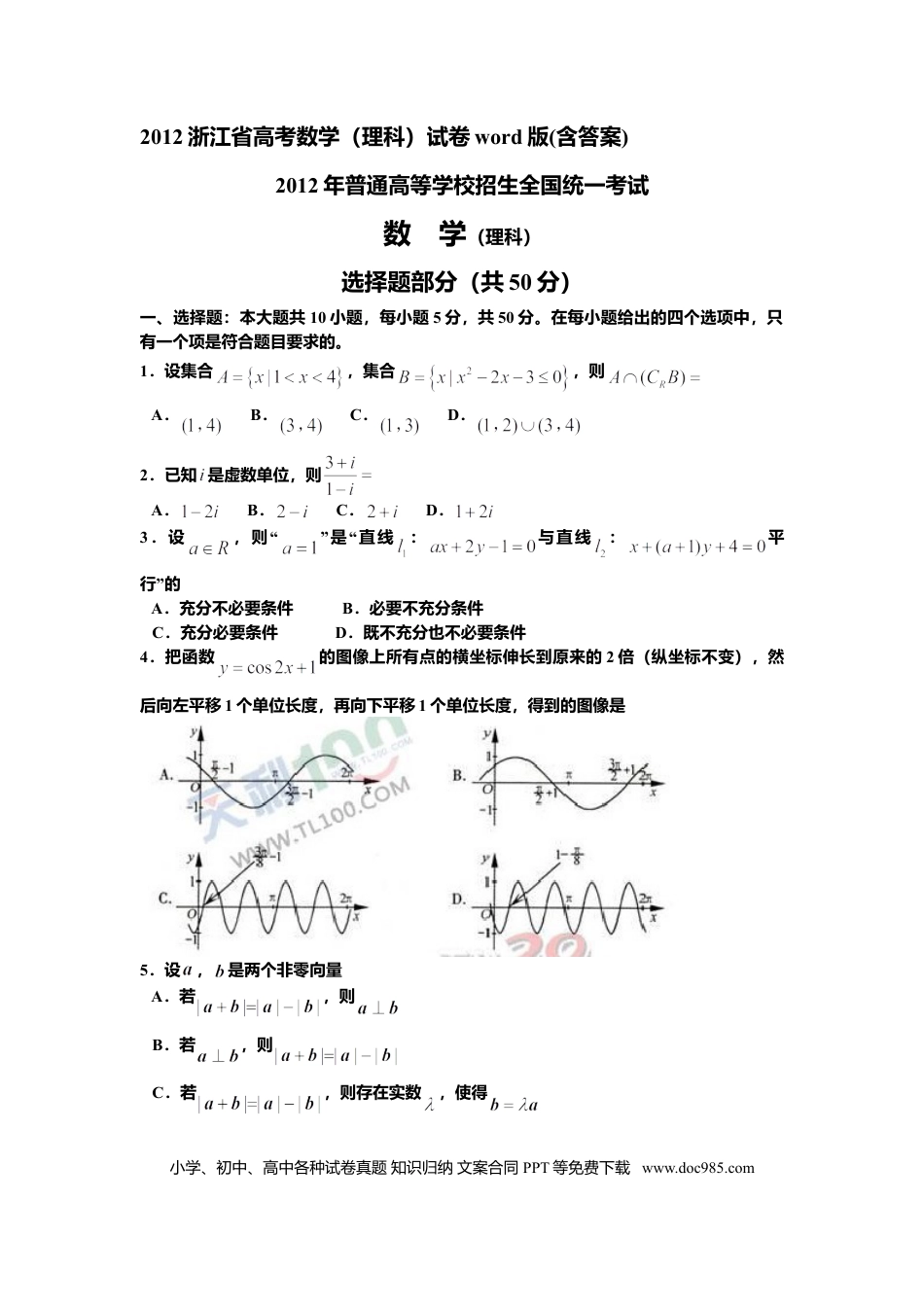
2012浙江省高考数学（理科）试卷word版(含答案)2012年普通高等学校招生全国统一考试数学（理科）选择题部分（共50分）一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一个项是符合题目要求的。1．设集合，集合，则A．B．C．D．2．已知是虚数单位，则A．B．C．D．3．设“，则”“是直线：与直线：平”行的A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件4．把函数的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是5．设，是两个非零向量A．若，则B．若，则C．若，则存在实数，使得小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comD．若存在实数，使得，则6．若从1，2，3…，，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有A．60种B．63种C．65种D．66种7．设是公差为（）的无穷等差数列的前项和，则下列命题错误的是A．若，则数列有最大项B．若数列有最大项，则C．若数列是递增数列，则对任意，均有D．若对任意，均有，则数列是递增数列8．如图，，分别是双曲线：的左、右两焦点，是虚轴的端点，直线与的两条渐近线分别交于，两点，线段的垂直平分线与轴交于点．若，则的离心率是A．B．C．D．9．设，A．若，则B．若，则C．若，则D．若，则10．已知矩形，，．将沿矩形的对角线所在的直线进行翻折，在翻折过程中，A．存在某个位置，使得直线与直线垂直B．存在某个位置，使得直线与直线垂直C．存在某个位置，使得直线与直线垂直D“．对任意位置，三对直线与”“，与”“，与”均不垂直小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com非选择题部分（共100分）二、填空题：本大题共7小题，每小题4分，共28分。11．已知某三棱锥的三视图（单位：）如图所示，则该三棱锥的体积等于．12．若某程序框图如图所示，则该程序运行后输出的值是．13．设公比为的等比数列的前项和为．若，，则．14．若将函数表示为，其中，，…，，为实数，则．15．在中，是的中点，，，则．16．定义：曲线上的点到直线的距离的最小值称为曲线到直线的距离．已知曲线：到直线：的距离等于曲线：到直线：的距离，则实数．17．设，若时均有，则．三、解答题：本大题共5小题，共72分。解答应写出文字说明、证明过程或演算步骤。18．（本题满分14分）在中，内角，，的对边分别为，，．已知，．Ⅰ（）求的值；Ⅱ（）若，求的面积．19．（本题满分14分）已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分．现从箱中任取（无放回，且每球取道的机会均等）3个球，记随机变量为取出此3球所得分数之和．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comⅠ（）求的分布列；Ⅱ（）求的数学期望．20．（本题满分15分）如图，在四棱锥中，底面是边长为的菱形，，且平面，，，分别为，的中点．Ⅰ（）证明：平面；Ⅱ（）过点作，垂足为点，求二面角的平面角的余弦值．21．（本题满分15分）如图，椭圆：的离心率为，其左焦点到点的距离为，不过原点的直线与相交于，两点，且线段被直线平分．Ⅰ（）求椭圆的方程；Ⅱ（）求面积取最大值时直线的方程．22．（本题满分14分）已知，，函数．Ⅰ（）证明：当时，（i）函数的最大值为；（ii）；Ⅱ（）若对恒成立，求的取值范围．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com