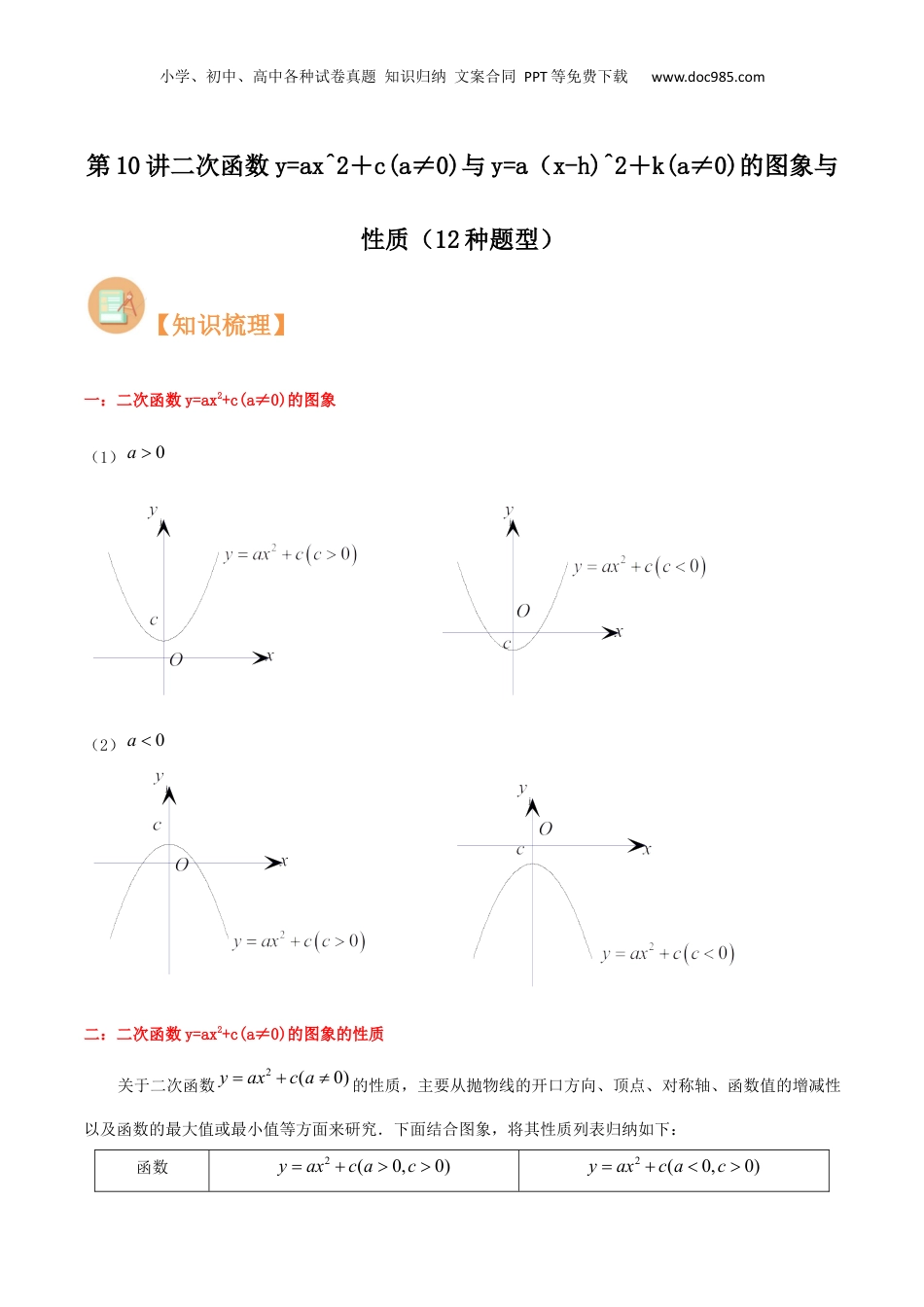
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第10讲二次函数y=ax^2＋c(a≠0)与y=a（x-h)^2＋k(a≠0)的图象与性质（12种题型）【知识梳理】一：二次函数y=ax2+c(a≠0)的图象（1）0a（2）0a二：二次函数y=ax2+c(a≠0)的图象的性质关于二次函数2(0)yaxca的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：函数2(0,0)yaxcac2(0,0)yaxcacjjjj小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图象开口方向向上向下顶点坐标(0，c)(0，c)对称轴y轴y轴函数变化当0x时，y随x的增大而增大；当0x时，y随x的增大而减小.当0x时，y随x的增大而减小；当0x时，y随x的增大而增大.最大（小）值当0x时，yc最小值当0x时，yc最大值三：二次函数20yaxa与20yaxca之间的关系；（上加下减）.20yaxa的图象向上（c＞0）【或向下（c＜0）】平移│c│个单位得到20yaxca的图象.要点诠释：抛物线2(0)yaxca的对称轴是y轴，顶点坐标是(0，c)，与抛物线2(0)yaxa的形状相同．函数2(0)yaxca的图象是由函数2(0)yaxa的图象向上（或向下）平移||c个单位得到的顶点坐标为(0，c)．抛物线y＝ax2(a≠0)的对称轴、最值与顶点密不可分，其对称轴即为过顶点且与x轴垂直的一条直线，其顶点横坐标x＝0，抛物线平移不改变抛物线的形状，即a的值不变，只是位置发生变化而已．四：二次函数的图像一般地，二次函数的图像是抛物线，称为抛物线，它可以通过将抛物线向左（时）或向右（时）平移个单位得到．抛物线（其中a、m是常数，且）的对称轴是过点（-m，0）且平行（或重合）于y轴的直线，即直线x=-m；顶点坐标是（-m，0）．当时，开口向上，顶点是抛物线的最低点；当时，开口向下，顶点是抛物线的最高点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com五：二次函数的图像二次函数（其中a、m、k是常数，且）的图像即抛物线，可以通过将抛物线进行两次平移得到．这两次平移可以是：先向左（时）或向右（时）平移个单位，再向上（时）或向下（时）平移个单位．利用图形平移的性质，可知：抛物线（其中a、m、k是常数，且）的对称轴是经过点（，0）且平行于y轴的直线，即直线x=；抛物线的顶点坐标是（，k）．抛物线的开口方向由a所取值的符号决定，当时，开口向上，顶点是抛物线的最低点；当时，开口向下，顶点是抛物线的最高点．【考点剖析】题型1：求二次函数y=ax2+c(a≠0)解析式例1.求下列抛物线的解析式：（1）与抛物线2132yx形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线；（2）顶点为（0，1），经过点（3，-2）并且关于y轴对称的抛物线．题型2：二次函数y=ax2+c(a≠0)平移例2.在同一直角坐标系中，画出2yx和21yx的图象，并根据图象(如图所示)回答下列问题．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)抛物线21yx向________平移________个单位得到抛物线2yx；(2)抛物线，21yx开口方向是________，对称轴为________，顶点坐标为________；(3)抛物线21yx，当x________时，随x的增大而减小；当x________时，函数y有最________值，其最________值是________．【变式】(1)抛物线225yx的开口方向，对称轴是，顶点坐标是．(2)抛物线2yaxc与23yx的形状相同，其顶点坐标为（0，1），则其解析式为．(3)抛物线2172yx向平移个单位后，得到抛物线2132yx.题型3：二次函数y=ax2+c(a≠0)的实际应用例3.有一个抛物线形的拱形隧道，隧道的最大高度为6m，跨度为8m，把它放在如图所示的平面直角坐标系中．（1）求这条抛物线所对应的函数关系式；（2）若要在隧道壁上点P（如图）安装一盏照明灯，灯离地面高4.5m．求灯与点B的距离．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型4：二次函数y=ax2+c(a≠0)与一次函数的综合例4.在...