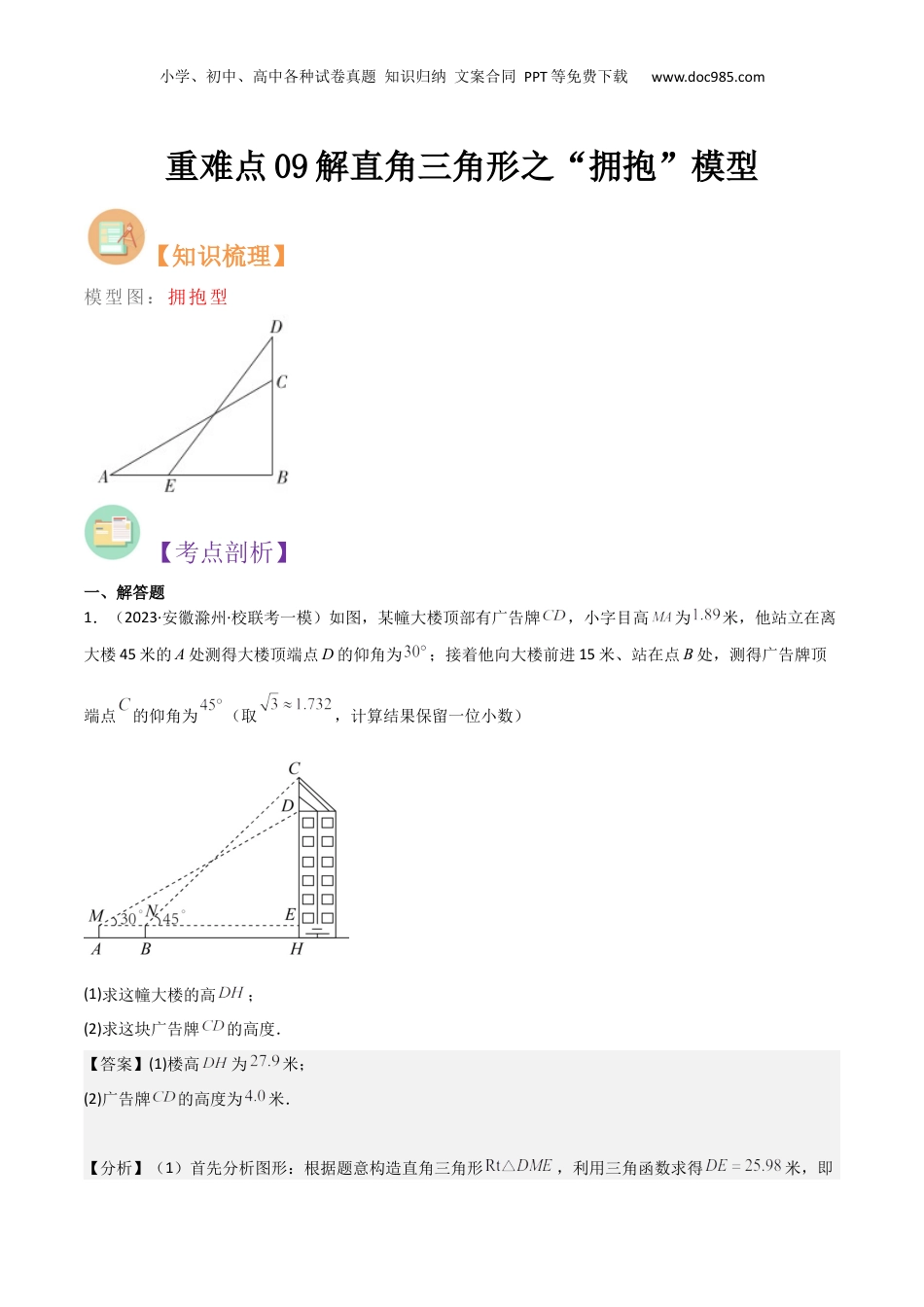
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点09解直角三角形之“拥抱”模型【知识梳理】模型图：拥抱型【考点剖析】一、解答题1．（2023·安徽滁州·校联考一模）如图，某幢大楼顶部有广告牌，小字目高为米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为；接着他向大楼前进15米、站在点B处，测得广告牌顶端点的仰角为（取，计算结果保留一位小数）(1)求这幢大楼的高；(2)求这块广告牌的高度．【答案】(1)楼高为米；(2)广告牌的高度为米．【分析】（1）首先分析图形：根据题意构造直角三角形，利用三角函数求得米，即小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com可得解；（2）根据题意构造直角三角形，利用三角函数求得米，即可得解．【详解】（1）解：在中，米；由，得米；又因为米，因而大楼米，答：楼高为米；（2）解： 在中，米，，∴米；因而广告牌米；答：广告牌的高度为米．【点睛】本题考查了解直角三角形的应用-仰角俯角问题，构造直角三角形是解题的关键．2．（2023·全国·九年级专题练习）如图所示，塑像DE在高54m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进22m到达B处，测得塑像顶部D的仰角为60°，求该塑像DE的高度．（精确到1m，参考数据；sin34°≈0.5，cos34°≈0.8，tan34°≈0.6，≈1.73）【答案】64m【分析】利用直角三角形的边角关系，在两个直角三角形中设未知数列方程求解即可．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】解：由题意可得，EC＝54m，AB＝22m，∠DBC＝60°，∠EAC＝34°，设DE＝xm，则DC＝（x+54）m，在Rt△DCB中， tan∠DBC＝，即＝，∴BC＝，在Rt△ECA中， tanA＝，∴AC＝≈＝90（m），由题意得，90﹣（x+54）＝22，解得，x≈64，答：塑像DE的高度约为64m．【点睛】本题考查解直角三角形的实际应用，掌握直角三角形的边角关系是正确解答的前提．3．（2019·河南·统考中考真题）数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE在高55m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进21m到达B处，测得塑像顶部D的仰角为60°，求炎帝塑像DE的高度．（精确到1m．参考数据：，，，）【答案】51小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】由三角函数求出，得出，在中，由三角函数得出，即可得出答案．【详解】解：，，，，，，，在中，，，，答：炎帝塑像DE的高度约为51m．【点睛】本题考查了解直角三角形的应用，解答本题的关键是根据仰角和俯角构造直角三角形，利用三角函数的知识求解，难度适中．4．（2020·陕西·九年级专题练习）如图，某公园的人工湖边上有一座假山，假山顶上有一座高为5米的建筑物CD，数学小组为了测量假山DE的高度，在公园找了一水平地面，在A处测得建筑物底部D点（即假山顶）的仰角为30°，沿水平方向前进25米到达B点，测得建筑物顶部C点的仰角为45°，点A，B，C，D，E在同一平面内，求假山DE的高度．（结果保留根号）【答案】假山DE的高度为（15+15）米．【分析】可先设假山DE的高度为x，得到CE=DE+CD=x+5，再根据直角三角形得到AE=AB+BE=30+x，然后直接运用三角函数解答即可小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】解：设假山DE的高度为x，则CE=DE+CD=x+5，在Rt△BCE中， ∠CBE=45°，∴BE=CE=x+5，∴AE=AB+BE=30+x，在Rt△ADE中， ∠DAE=30°，DE=x，∴AE==x，解答：x=15+15，答：假山DE的高度为（15+15）米．【点睛】此题考查直角三角形的性质和三角函数的应用，解题关键是设假山DE的高度为x，再进行求解5．（2020秋·河南郑州·九年级河南省实验中学校考阶段练习）数学兴趣小组到黄河风景名胜区测量炎帝塑像（塑像中高者）的高度．如图所示，炎帝塑像DE在高54m的小山EC上，在A处测得塑像底部E的仰角为34°，再沿AC方向前进22m到达B处，测得塑像顶部D的仰角为60°．（1）求炎帝塑像DE的高度．（精确到1m．参考数据：sin34°≈0.5，cos34°...