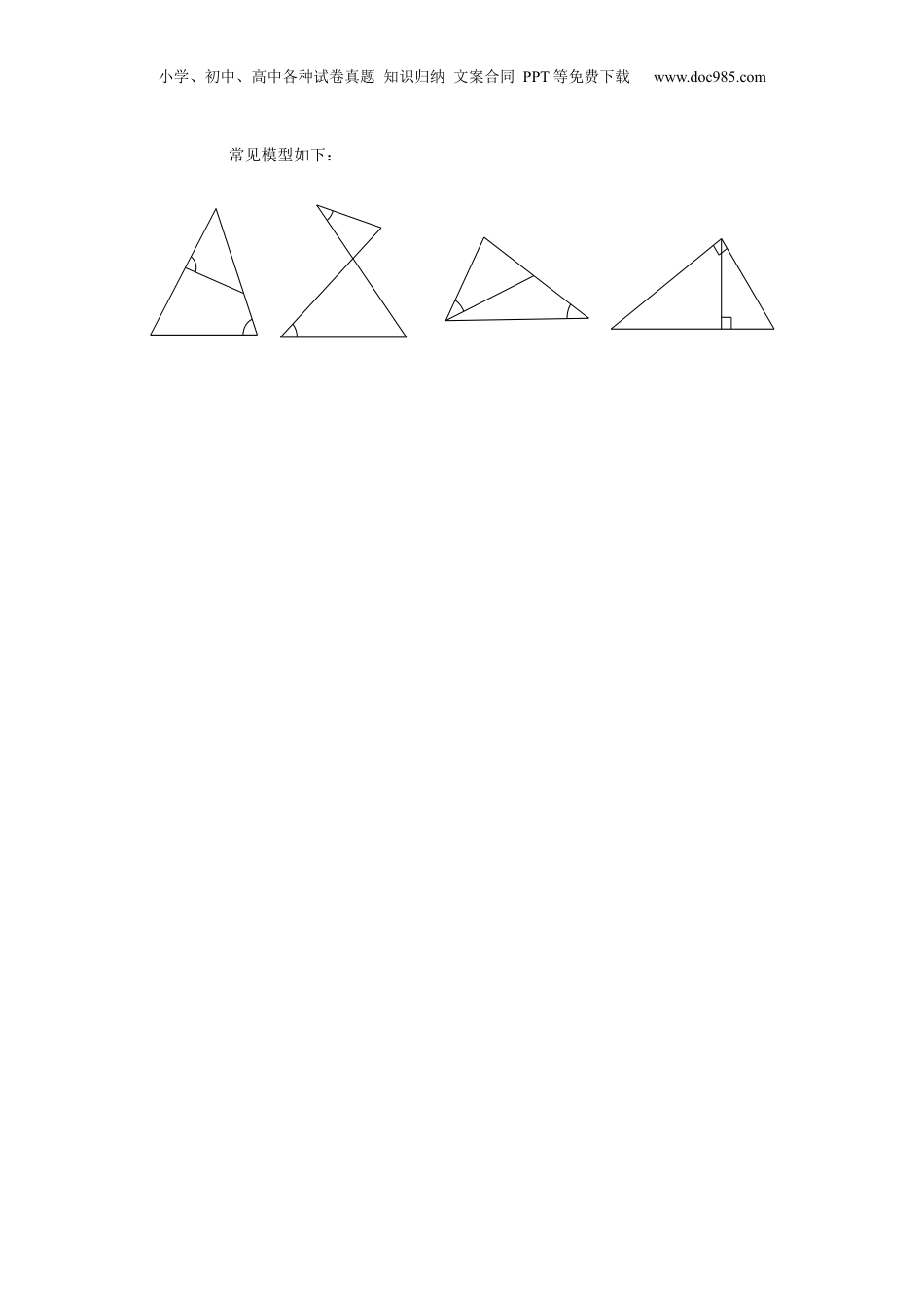
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com相似三角形的判定（一）相似三角形的判定是九年级数学上学期第一章第三节的内容，本讲主要讲解相似三角形的定义、相似三角形判定定理1和相似三角形判定定理2；重点是根据已知条件灵活运用这两种判定定理，以及这两者之间的相互结合．1、相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等，且它们各有的三边对应成比例，那么这两个三角形叫做相似三角形．如图，是的中位线，那么在与中，，，；．由相似三角形的定义，可知这两个三角形相似．用符号来表示，记作，其中点与点、内容分析知识结构模块一：相似三角形判定定理1知识精讲ECBAD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com点与点、点与点分别是对应顶点；符号“”读作“相似于”．用符号表示两个相似三角形时，通常把对应顶点的字母分别写在三角形记号“”后相应的位置上．根据相似三角形的定义，可以得出：（1）相似三角形的对应角相等，对应边成比例；两个相似三角形的对应边的比，叫做这两个三角形的相似比（或相似系数）．（2）如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似．2、相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似．如图，已知直线与的两边、所在直线分别交于点和点，则．3、相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似．可简述为：两角对应相等，两个三角形相似．如图，在与中，如果、，那么．C1B1A1CBAEDCBAEDCBAEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com常见模型如下：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例1】如图，是平行四边形的边延长线上的一点，交于点．图中有哪几对相似三角形？【例2】如图，，那么图中相似的三角形有哪几对？【例3】如图，在中，，于点，且，求的值．【例4】如图，中，，是中点，交延长线于点，则相似于．FEDCBA321EDCBACDBAEDCBA例题解析小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例5】如图，，于点，，，求的长．【例6】如图，，，点在线段上运动，，，，若与相似，求的值．【例7】如图，是等边三角形，，求证．【例8】正方形中，是中点，于点，厘米，求的长．EDCBAEDCBAEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例9】如图，在中，，于点，点是边上一点，联结交于点，交边于点．求证：．【例10】如图，在中，，，是内一点，且．求证：．【例11】如图，在中，，//，点在边上，与相OFEDCBAPCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com交于点，且．（1）求证：；（2）．【例12】如图，已知、均为等边三角形，、分别在边、上，请找出一个与相似的三角形，并加以证明．【例13】如图，矩形的对角线、相交于点，于点，交于点，交的延长线于点．求证：．GFEDCBAHGFEDCBAOFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例14】如图，中，，是中线，是上一点，过作//，延长交于点，交于点．求证：．【例15】如图，在中，，，点在边上，点在线段上，且，的延长线与边相交于点．（1）求证：；（2）设，，求关于的函数解析式，并写出定义域．FEDCBAPFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．可简述为：两边对应成比例且夹角相等，两个三角形相似．如图，在与中，，，那么．A1A模块二：相似三角形判定定理2知识精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例16】如图，在与中，，．求证：．【例17】下列说法一定正确的是（）A．有两边对应成比例且一角相等的两个三角形相似B．对应角相等的两个三角形不一定相似C．...