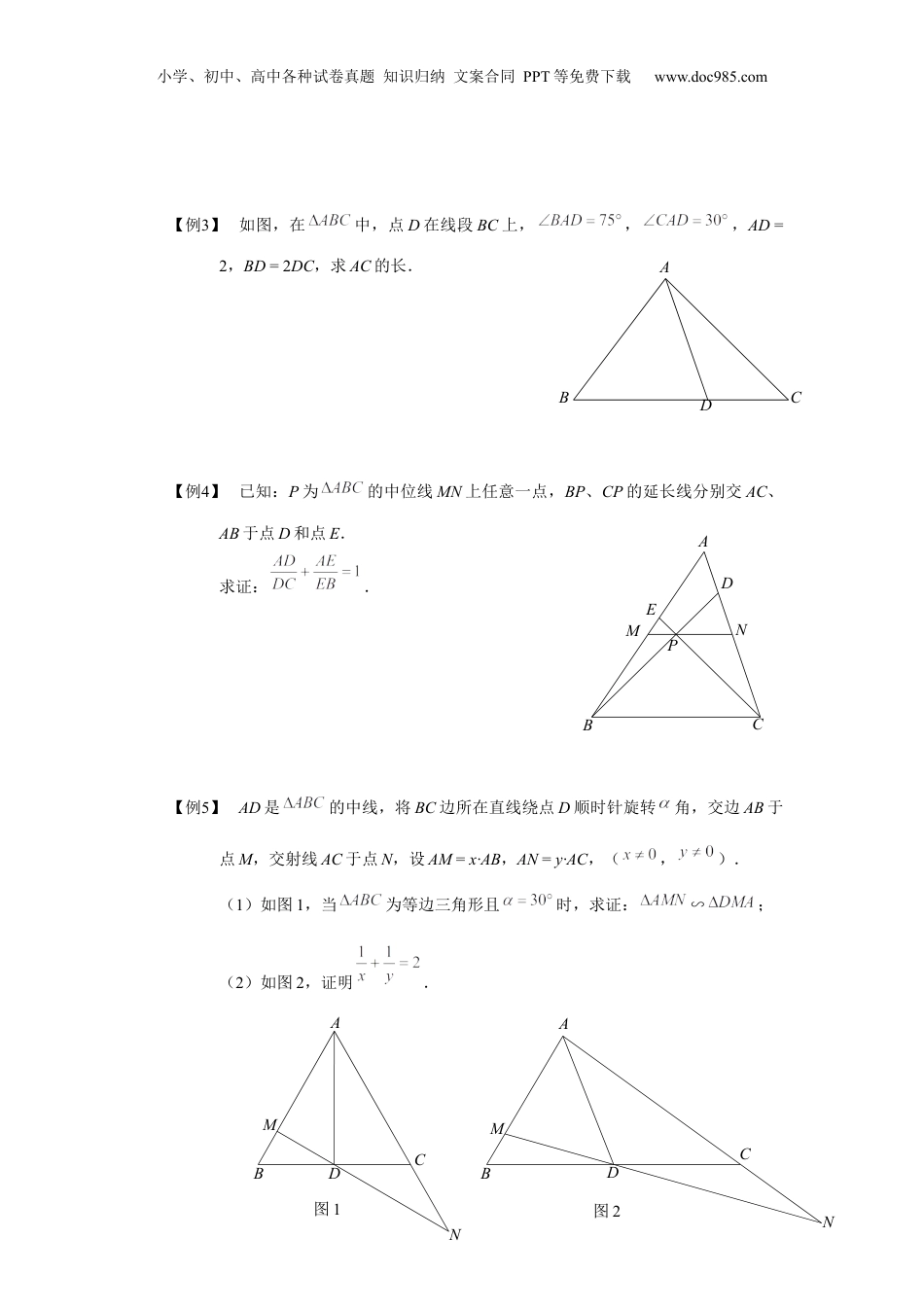
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com相似三角形是初中数学中的重点，也是难点．相当多的知识点可以与相似三角形综合起来考察．本讲将从以下几个方面学习相似三角形的应用，旨在灵活运用相似三角形的判定和性质解决问题．相似三角形综合内容分析知识结构小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、平行线与相似三角形利用平行线构造的相似主要有两个基本的模型，即：“A”字型和“X”字型．【例1】过的顶点C任作一直线，与边AB及中线AD分别交于点F、E．求证：【例2】如图，已知中，AD、BE相交于G，，．求的值．FEDCBAGEDCBA模块一：平行线与相似三角形知识精讲例题解析小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例3】如图，在中，点D在线段BC上，，，AD=2，BD=2DC，求AC的长．【例4】已知：P为的中位线MN上任意一点，BP、CP的延长线分别交AC、AB于点D和点E．求证：．【例5】AD是的中线，将BC边所在直线绕点D顺时针旋转角，交边AB于点M，交射线AC于点N，设AM=x·AB，AN=y·AC，（，）．（1）如图1，当为等边三角形且时，求证：∽；（2）如图2，证明．DCBAMNPEDCBA图2图1MNDCBAMNDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、角平分线与相似三角形角平分线类的相似模型如下：分为“内角平分线”和“外角平分线”两种类型，虚线部分为辅助线的作法．【例6】如图，AD是的内角平分线．求证：．【例7】如图，AD是的外角平分线．求证：．DCBADCBA模块二：角平分线与相似三角形知识精讲例题解析小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例8】在中，，AD平分交BC于点D．求证：．【例9】如图，在中，，过点C作CE//AB，交的平分线AD于E．（1）不添加字母，找出图中所有的相似三角形，并证明；（2）求证：．【例10】如图，中，AI、BI分别平分、，CE是的外角的平分线，交BI延长线于E，连接CI．（1）变化时，设．若用表示和，那么______，______；（2）若AB=1，且与相似，求AC长．DCBAGFEDCBAIECBAD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、a2=b·c与相似三角形常见及扩展模型如下：由图1可证：；由图2可证：，，．【例11】如图，中，，于点D．求证：．【例12】如图，已知等腰三角形ABC中，AB=AC，高AD，BE相交于点H．求证：图2图1DCBADCABHEDCBA模块三：a2=b·c与相似三角形知识精讲例题解析DCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例13】如图，在直角梯形ABCD中，AB//CD，ABBC，对角线ACBD，垂足为E，AD=BD，过E的直线EF//AB交AD于点F．（1）AF=BE；（2）AF2=AE·EC．【例14】如图，在中，AD平分，AD的垂直平分线交AB于点E，交AD于点H，交AC于点G，交BC的延长线于点F．求证：．【例15】如图1，在中，P是边AB上的一点，联结CP，要使∽，还需要补充一个条件．（1）补充的条件是___________________，或者____________________．（2）请你参考上面的图形和结论，解答下面的问题：如图2，在中，，，求的度数．FEDCBAHGFEDCBA图2图1PCBACBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、内接矩形与相似三角形相关模型：常用结论：．【例16】如图，中，，，，四边形DEFG为正方形，其中D、E在边AC、BC上，F、G在AB上，求正方形DEFG的边长．【例17】中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，BC=15，BC边上的高AD=10，求正方形EFGH的面积．THGFEDCBAGFEDCBADEFGHCBA模块四：内接矩形与相似三角形知识精讲例题解析小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例18】如图，已知中，AC=3，BC=4，，在内部求做一正方形，...