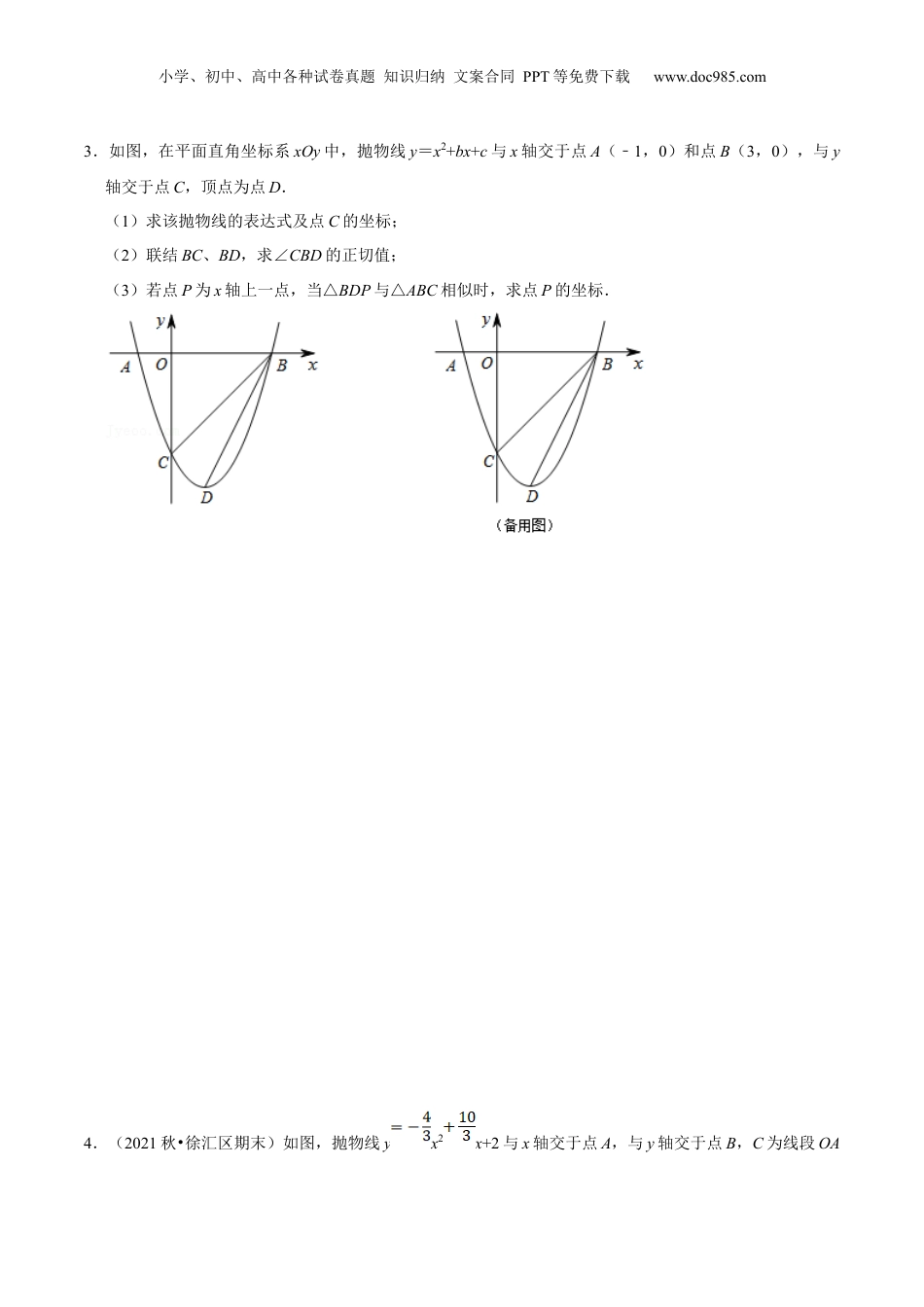
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第15讲二次函数中相似三角形的存在性（核心考点讲与练）【基础知识】二次函数背景下的相似三角形考点分析：1.先求函数的解析式，然后在函数的图像上探求符合几何条件的点；2.简单一点的题目，就是用待定系数法直接求函数的解析式；3.复杂一点的题目，先根据图形给定的数量关系，运用数形结合的思想，求得点的坐标，继而用待定系数法求函数解析式；4.还有一种常见题型，解析式中由待定字母，这个字母可以根据题意列出方程组求解；5.当相似时：一般说来，这类题目都由图像上的点转化到三角形中的边长的问题，再由边的数量关系转化到三角形的相似问题；6.考查利用几何定理和性质或者代数方法建立方程求解的方法。【考点剖析】1．（2022春•虹口区校级期中）如图，在平面直角坐标系xOy中，直线y＝x3﹣分别交x轴、y轴于A、B两点，抛物线y＝x2+bx+c经过点A和点B，且其顶点为D，点C为抛物线与x轴的另一个交点．（1）求抛物线的表达式；（2）求∠BAD的正切值；（3）点P在抛物线上，若∠PAC＝∠BAD，求点P的坐标．（4）联结BC，延长DB交x轴于点E，点Q是直线y＝x3﹣上的动点，如果△QBC与△AED是相似三角形，求点Q的坐标．2．（2022春•杨浦区校级月考）已知矩形OABC在平面直角坐标系中的位置如图所示，A、C两点的坐标小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com分别为A（6，0），C（0，3），直线yx与边BC相交于点D．（1）求点D的坐标；（2）若抛物线y＝ax2+bx（a≠0）经过A、D两点，试确定此抛物线的解析式；（3）在（2）中的抛物线的对称轴与直线AD交于点M，点P在对称轴上，且△PAM与△ABD相似，求点P的坐标．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3．如图，在平面直角坐标系xOy中，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，顶点为点D．（1）求该抛物线的表达式及点C的坐标；（2）联结BC、BD，求∠CBD的正切值；（3）若点P为x轴上一点，当△BDP与△ABC相似时，求点P的坐标．4．（2021秋•徐汇区期末）如图，抛物线yx2x+2与x轴交于点A，与y轴交于点B，C为线段OA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com上的一个动点，过点C作x轴的垂线，交直线AB于点D，交该抛物线于点E．（1）求直线AB的表达式，直接写出顶点M的坐标；（2）当以B，E，D为顶点的三角形与△CDA相似时，求点C的坐标；（3）当∠BED＝2∠OAB时，求△BDE与△CDA的面积之比．5．（2021•静安区二模）在平面直角坐标系xOy中，点A的坐标为（5，0）（如图），经过点A的抛物线y＝x2+bx+5与y轴相交于点B，顶点为点C．（1）求此抛物线表达式与顶点C的坐标；（2）求∠ABC的正弦值；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（3）将此抛物线向上平移，所得新抛物线的顶点为D，且△DCA与△ABC相似，求平移后的新抛物线的表达式．【过关检测】1.（2022青浦一模24）如图，在平面直角坐标系xOy中，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，顶点为点D．（1）求该抛物线的表达式及点C的坐标；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）联结BC、BD，求∠CBD的正切值；（3）若点P为x轴上一点，当△BDP与△ABC相似时，求点P的坐标．2.（2022嘉定一模24）（12分）（2021秋•嘉定区期末）在平面直角坐标系xOy中，点A、B两点在直线y＝x上，如图．二次函数y＝ax2+bx﹣2的图象也经过点A、B两点，并与y轴相交于点C，如果BC∥x轴，点A的横坐标是2．（1）求这个二次函数的解析式；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）设这个二次函数图象的对称轴与BC交于点D，点E在x轴的负半轴上，如果以点E、O、B所组成的三角形与△OBD相似，且相似比不为1，求点E的坐标；（3）设这个二次函数图象的顶点是M，求tan∠AMC的值．3（202崇明一模）24.如图，抛物线y=−x2+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，...