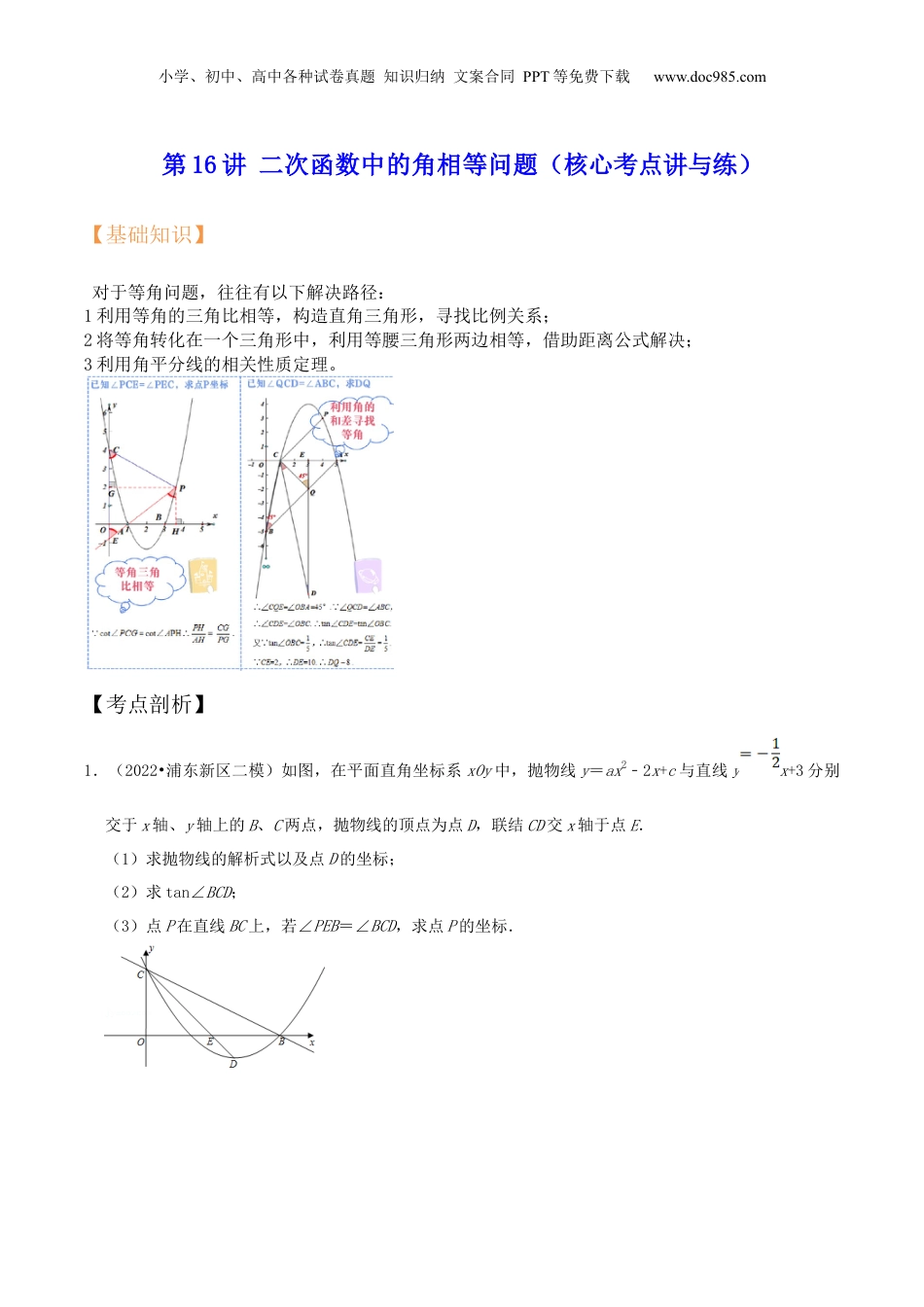
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第16讲二次函数中的角相等问题（核心考点讲与练）【基础知识】对于等角问题，往往有以下解决路径：1利用等角的三角比相等，构造直角三角形，寻找比例关系；2将等角转化在一个三角形中，利用等腰三角形两边相等，借助距离公式解决；3利用角平分线的相关性质定理。【考点剖析】1．（2022•浦东新区二模）如图，在平面直角坐标系xOy中，抛物线y＝ax2﹣2x+c与直线yx+3分别交于x轴、y轴上的B、C两点，抛物线的顶点为点D，联结CD交x轴于点E．（1）求抛物线的解析式以及点D的坐标；（2）求tan∠BCD；（3）点P在直线BC上，若∠PEB＝∠BCD，求点P的坐标．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2022春•静安区期中）在平面直角坐标系中，已知抛物线与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3），对称轴为直线x＝1，交x轴于点E．（1）求该抛物线的表达式；（2）点D为此抛物线的顶点，证明：∠CDB＝∠CAB；（3）在x轴上是否存在一点M，以及抛物线上一点N，使得以M、N、B、C四点构成的四边形为平行四边形？如果有，请直接写出点M的坐标；如果没有，请说明理由．3．（2022•黄浦区校级二模）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2ax+c（a＞0）与x轴交于点A（﹣2，0）、B两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，直线小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com经过点A，交抛物线的对称轴于点E．（1）求△ABE的面积；（2）联结EC，交x轴于点F，联结AC，若，求抛物线的表达式；（3）在（2）的条件下，点P是直线AE上一点，且∠EPB＝∠ECB，求点P的坐标．4．（2020•浦东新区三模）在平面直角坐标系xOy中，已知抛物线y＝﹣x2+bx+c与x轴交于点A（﹣3，0）和点B，与y轴相交于点C（0，3），抛物线的顶点为点D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）求抛物线的表达式及顶点D的坐标；（2）联结AD、AC、CD，求∠DAC的正切值；（3）如果点P是原抛物线上的一点，且∠PAB＝∠DAC，将原抛物线向右平移m个单位（m＞0），使平移后新抛物线经过点P，求平移距离．【过关检测】1.（2022长宁一模24）抛物线与轴相交于两点(点在点左侧),与轴交小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com于点,其顶点的纵坐标为4．（1）求该抛物线的表达式；（2）求的正切值；（3）点在线段的延长线上,且,求的长．2.（2022黄埔一模24）如图，在平面直角坐标系中，抛物线与轴交于小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com两点与轴交于点C，点M是抛物线的顶点，抛物线的对称轴与BC交于点D，与轴交于点E．（1）求抛物线的对称轴及B点的坐标（2）如果，求抛物线的表达式；（3）在（2）的条件下，已知点F是该抛物线对称轴上一点，且在线段的下方，，求点的坐标小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3.（2022年松江一模24题）如图，已知直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c经过A、B两点．（1）求这条抛物线的表达式；（2）直线x＝t与该抛物线交于点C，与线段AB交于点D（点D与点A、B不重合），与x轴交于点E，联结AC、BC．①当＝时，求t的值；②当CD平分∠ACB时，求ABC的面积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4.（2021年长宁二模）如图，已知在平面直角坐标系xOy中，抛物线y＝ax2﹣x+c经过点A（1，0）、B（3，0），且与y轴交于点C．（1）求抛物线的表达式；（2）如果将抛物线向左平移m（m＞0）个单位长度，联结AC、BC，当抛物线与△ABC的三边有且只有一个公共点时，求m的值；（3）如果点P是抛物线上一动点，且在点B的右侧，联结PC，直线PA交y轴于点E，当∠PCE＝∠PEC时，求点P的坐标．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5.（2021年杨浦二模）如图，已知在平面直角坐标系xOy中，直线y＝x﹣5与x轴...